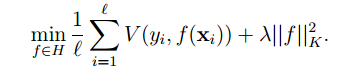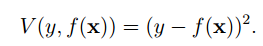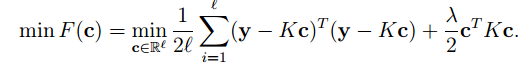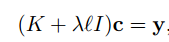在機器學習或者是模式識別當中有一種重要的分類器叫做：SVM 。這個被廣泛的應用於各個領域。但是其計算的複雜度以及訓練的速度是制約其在實時的計算機應用的主要原因。因此也很很多的演算法被提出來，如SMO，Kernel的方法。

但是這裡要提到的 Regularized least-squares classification 是一個和他有著同樣的效果的分類器。比較而言計算卻比較的簡單（We see that a Regularized Least-Squares Classification problem can be solved by solving a single system of linear
equations.）。接下來將對其進行介紹。

首先我們知道最終要求得的結果是： f（x）= <W, x> +b 

策略函式：

我們還是要來看一下他的策略：結構風險最小化Function。

通過使用kernel的方法將x 投影到希爾伯特空間（只需要隱式的表示）得到的結果是：

                                                                             （ 這裡的alpha就是下面的c啦！）

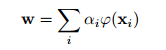
帶入到目標函式以及簡化，我們得到最終要求的函式 f*(x

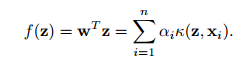
這就是最終要求的結果。後面額的核函式我們可以採用一些常用的核函式處理掉（比如說：高斯核（Gaussian Kernel）等）。那如何來解決ci勒？

如何解c：

大家都知道在SVM當中採用的是合頁損失函式（hinge loss Function）。但是很顯然這裡是平方損失函式：

同時我們對於上面的f*（x）帶入到最開始的策略函式當中：

於是我們再來通過求導，令導數等於0，解出這個方程：

有沒有發現異常的簡單啊！

這裡要注意的是： K 是一個n*n的方陣，對於訓練來講，沒兩個樣本（投影到高維空間後）都要做內積才能夠得到K。

但其實作者也說了，可以通過一個線性的問題來解決並不意味著它的時間複雜度和空間複雜度就小了：訓練一個Kernel的時間還是需要很長的。同時也需要較大的空間來儲存下這樣的核：K。但是仍舊是可以通過一些的方法來明顯的提高它的效能的。

結果的比較：

文章中提到：It took 10,045 seconds (on a Pentium IV running at 1.5 GhZ) to train 20 one-vs-all SVMs, and only 1,309 seconds to train the equivalent RLSC classifiers. At test time, both SVM and RLSC yield a linear hyperplane, so testing times are equivalent. 足見速度可以達到SVM的速度的9倍左右，而精度卻可以達到相當的程度。

我們再來看一個測試的比較，下表表示的是兩種演算法在兩個資料集上面的錯誤率：

最上面的資料代表訓練的樣本數，下面書錯誤率。可以看得出來RLS的方法還是很好的。