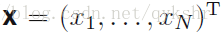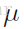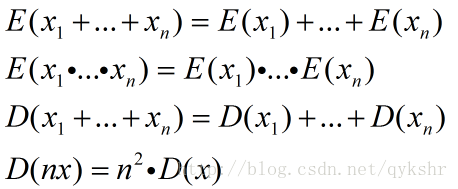本文要證明為什麼對高斯分佈的方差的極大似然估計是有偏的。同時，也說明為什麼求樣本方差時，分母是N-1而不是N。

首先，明白兩點，（1）極大似然法得到的高斯方差是什麼形式（2）什麼是有偏。

（1）先說第一個問題，用極大似然估計得到的高斯方差是什麼。

假設有n個符合高斯獨立同分布的觀測值

，我們要根據這些樣本值估計正態分佈的期望和方差。

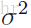
以上資訊可以表示為：

（1）

極大似然估計就要找需要合適的和使得（1）式具有最大值。

對上式兩邊同時取對數，得

（2）

取對數操作的好處：1、log函式在定義域上是單調函式，便於求極值 2、便於計算機計算，因為過小的值做乘法運算可能會導致溢位，取對數操作之後，將乘法轉換為加法，避免了這個問題。

對（2）式右邊對求偏導，並令導數值為零，解得

（3）

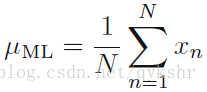
對（2）式右邊對求偏導，並令導數值為零，解得

（4）。

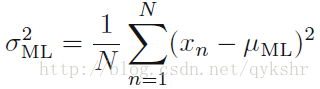
現在得到期望和方差的表達形式了，接下來判斷他們是否有偏。

（2）有偏與無偏

如果一個變數的期望等於他的理想值，那麼就稱該變數無偏；否則稱為有偏。

在下面的證明中，會用到多變數和、積的期望以及多變數和、積的方差公式：

當多個變數相互獨立時，有

另外，

，因為，是的一個例項，服從什麼分佈，當然也服從。

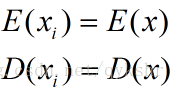
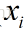
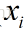
預備知識講完了，下面開始證明：

對於期望估計有，

（5）

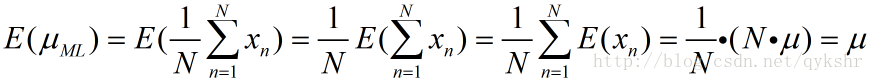
對於方差估計則比較麻煩一些，

首先，對平方進行展開，再進行一些合併

（6）

接著，分別求其中的後兩項

（7）

（8）

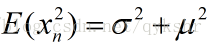
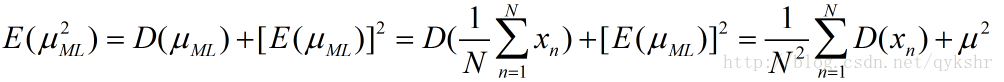
最後，將（7）、（8）式帶入（6）式，得

（9）

終於大功告成，所以均值估計是無偏的，方差估計是有偏的。那麼無偏的方差估計應該是什麼形式？

答案是，

（10）

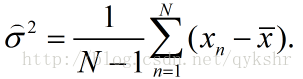
這也就是為什麼求樣本方差的時候分母是N-1而不是N。

這種形式的方差估計的無偏性讀者可以仿照上面進行證明。