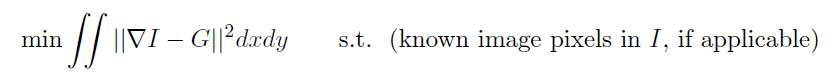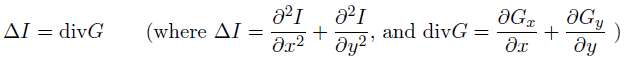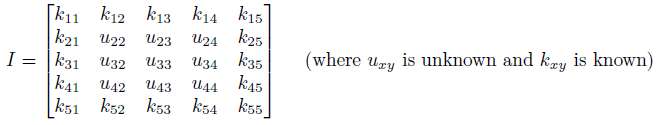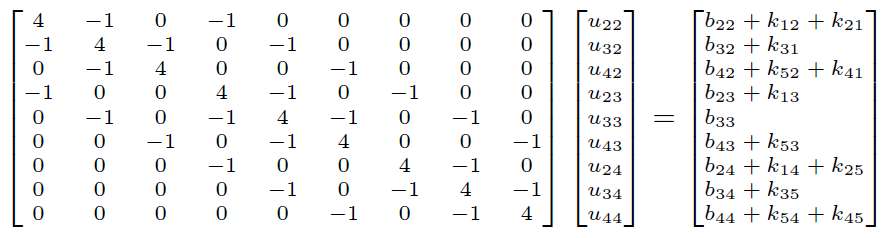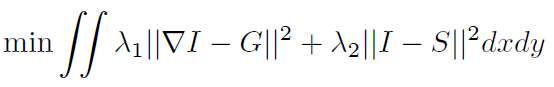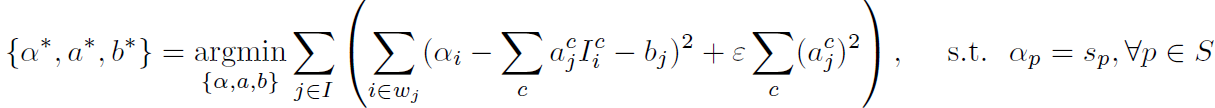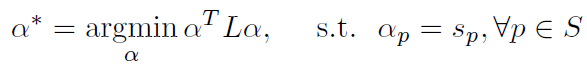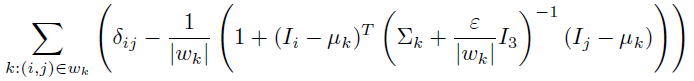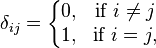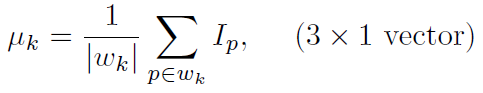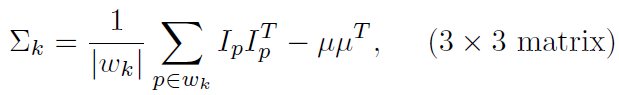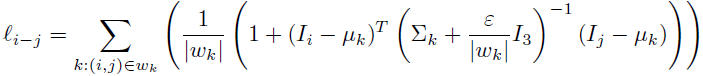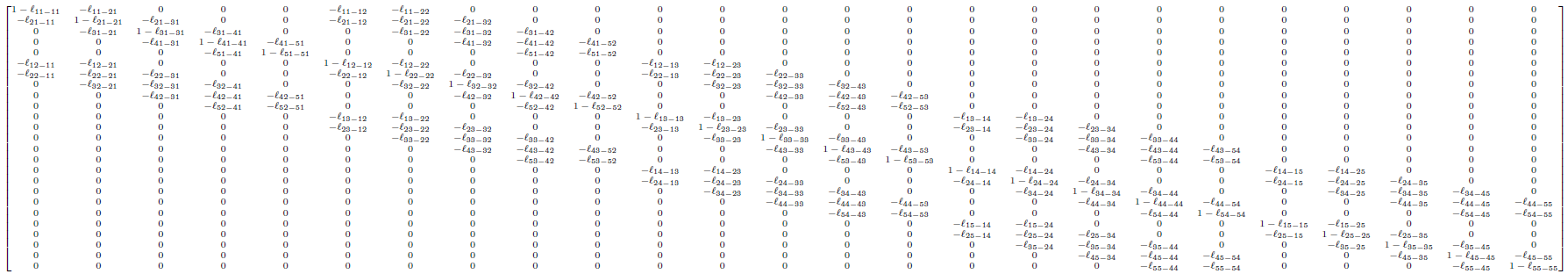影象處理中的全域性優化技術(Global optimization techniques in image processing and computer vision) (二)
原文:http://blog.csdn.net/mulinb/article/details/9079645
MulinB按:最近打算好好學習一下幾種影象處理和計算機視覺中常用的 global optimization (或 energy minimization) 方法,這裡總結一下學習心得。分為以下幾篇:
2. Quadratic Optimization: Poisson Equation and Laplacian Matrix (本篇)
2. Quadratic Optimization: Poisson Equation and Laplacian Matrix
Quadratic Optimization (Least Squares Minimization)在影象處理中的魅力要從SIGGRAPH 02和03年的兩篇Gradient Domain Image Editing文章說起:Fattal的HDR Compression[1] 和Perez的Poisson
Image Editing [2]。 其後,Levin的兩篇文章Colorization [3]和Closed-Form
Matting [4]更是將其魅力展現的淋漓盡致。而Farbman的基於Weighted Least Squares的WLS filter [5]也是在Edge-preserving
Filter領域名聲大噪。由於目標函式是quadratic, 這類問題的求解一般比較容易,大多都可以最終歸結為求解一個大型稀疏線性方程組。而數值求解大型線性方程組是一個由來已久的問題,有著各種現成的solver,更是有著為以上這類問題量身定做的solver,見下文solver小節。
題外話:以色列的耶路撒冷希伯來大學(The Hebrew University of Jerusalem)的Lischinski教授貌似很偏愛這類方法,上面提到的這些文章大多有他的署名。
2.1 Problem I: Gradient Domain Image Editing
有心理學為證(見Poisson Image Editing [2]文章的introduction部分),對影象的gradient進行修改可以產生比較不容易感知到的artifacts,這使得很多影象編輯的工作可以放到gradient domain使得效果很逼真,比如下圖的影象拼合例子(圖例來自[2]):
其實對gradient domain進行修改而獲得逼真的編輯效果由來已久,最早見於1983年Burt-Adelson的Laplacian Pyramid
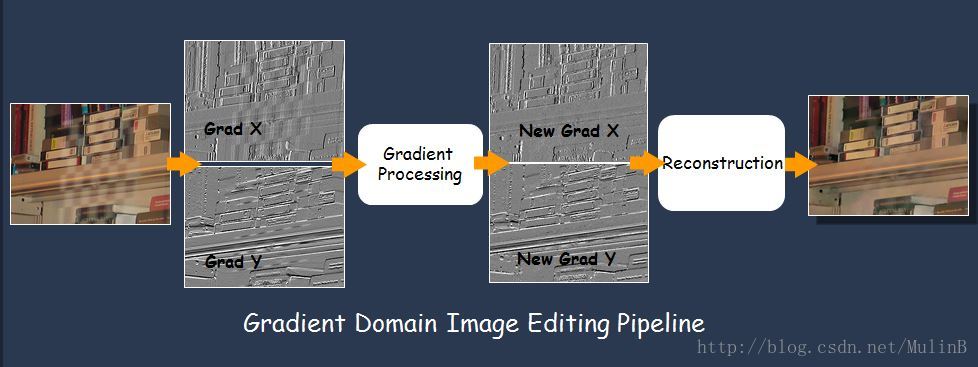
其中第一步的gradient processing根據不同的需求有具體的操作,比如HDR Compression裡是將較大的gradient value進行削弱,而上面的影象拼合例子(Seamless Clone)則是將源影象的gradient拷貝到目標區域。而其中第二步中由gradient重建出新影象並非那麼容易,因為經過編輯後的gradient一般是不可積分的,這時Quadratic Optimization粉墨登場。
假設待求影象為I,修改後的已知gradient是G,則通過Least Squares Minimization可以將問題formulate成如下(使得待求影象I的gradient在L2 norm下儘量接近G):
注意其中的約束條件,比如,在影象拼合例子中,非編輯區域的畫素是已知的,在求解編輯區域的畫素時,邊界上的畫素值是約束條件。上面的formulation是假設影象I是定義在x-y連續空間的函式,所以其實上述目標函式是關於I的functional(泛函,也就是“函式的函式”)。使用calculus of variation(變分法)中的Euler-Lagrange Equation (one unknown function, two variables)可以將其轉化為一個非常經典的偏微分方程形式,這就是Poisson Equation:
上面的formulation是在x-y連續空間(畫素座標是連續的),而用於影象處理時,一般需要將其離散化(因為事實上畫素座標(x,y)是整數),上面相應的偏微分形式可以使用有限差分(finite difference)形式近似代替。具體來講,離散化的discrete Laplacian operator如下,
而divergence operator中的一階偏導可以用前向或者後向差分近似(由於G本身是由gradient得來,一般如果之前計算gradient使用前向差分,那麼這裡計算div就使用後向差分,這樣使得兩次差分的結果等價於一次二階中心差分,具體參考[1]),比如這裡的divG可以由以下後向差分近似,
於是,整個Poisson Equation離散化之後,每個pixel都有一個線性方程,假設影象有N個pixel,那麼整個Poisson Equation就成了一個包含N個方程的大型方程組。如果將這個大型方程組寫成矩陣形式(假設將待求影象I拉成一個長的vector,用x表示,將已知的divG也拉成一個長的vector,用b表示),離散化的Poisson Equation變成了經典的Ax=b形式。以5×5的影象為例,假設待求影象I為如下形式(每個pixel的值都是未知):
將其拉成列向量x(按列展開),則整個Discrete Poisson Equation (with Neumann boundary condition)寫成Ax=b形式即,
該矩陣A可以直接從Laplacian operator得來,一般稱為Laplacian Matrix(其實如果將影象看成graph,該矩陣即為graph theory中的Laplacian
Matrix)。注意,對角線上值為2和3的元素是對應在影象邊界上的pixel(因為其discrete Laplacian operator無法完整展開,包含了一些不存在的neighboring pixel),如果將邊界條件改為Dirichlet boundary condition並且未知區域周邊的pixle都是已知的話,對角線上的元素就全為4,比如下面的例子。假設待求影象I為如下形式(未知pixel的周邊pixel是已知):
則未知向量x包含9個元素,整個Discrete Poisson Equation (with Dirichlet boundary condition)變成以下形式,
注意等式右側包含了邊界已知pixel的值。這裡的Laplacian Matrix較為規整,主要是因為所有的未知pixel處的discrete Laplacian operator可以完整的展開。
總之,上面的discrete Poisson Equation都可以歸結為求解一個大型線性方程組,其中的Laplacian Matrix具有以下特點:
1. 對角線元素為non-negative;
2. 非對角線元素為non-positive;
3. 對稱(symmetric);
4. 正定或半正定(positive semidefinite);
5. 屬於分塊對角陣。
下面的solver小節再討論如何求解這樣的線性方程組。另外,其實如果直接對上面Least Squares Minimization的目標函式進行離散化,也可以得到相同的方程組(省去了應用Euler-Lagrange Equation的步驟),參見文章[2]的推導過程。
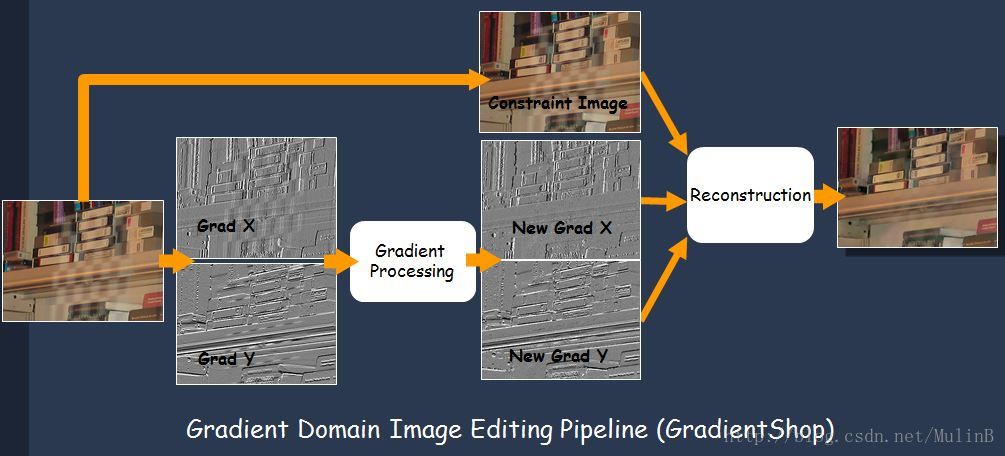
如果進一步對上述的Gradient Domain Image Editing Pipeline進行推廣,將原始影象考慮進來(注意,前面的方法是完全由新的gradient重建影象,不考慮原始影象的影響),這樣可以得到一個更為強大的framework,這就是GradientShop[7] (其實之前Levin的Colorization[3],以及Lischinski的Interactive Local Adjustment[8],和Farbman的WLS filter[5]都可以算作這個framework的特例),新的框架如下:
假設constraint image為影象S(可以是原始影象本身或者經過處理後的影象、使用者輸入的畫素值等),新的gradient為G,待求影象為I,則Least Squares Minimization的目標函式推廣為如下:
其中lambda為weighting factor,用來權衡constraint image和new gradient對待求影象的影響,可以整個image用統一的lambda值,也可以用一個weighting map為每個pixel賦上不同的lambda值。比如,在Levin的Colorization[3]中,待求的影象I是chrominance通道(比如YUV中的U和V通道),G=0,S是使用者輸入的scribbles,lambda_2是scribble的mask(有scribble為1,否則0),lambda_1是根據已知灰度圖中相鄰pixel的affinity進行賦值(pixel灰度值越相似,值越大),這樣獲得的Laplacian Matrix可以使得使用者輸入的scribble根據pixel affinity進行有效的propagation。再以5×5影象為例,假設影象M(元素為m_xy)為S的reverse mask(有輸入為0,沒有輸入為1),S的元素用s_xy表示(無使用者輸入處的pixel為0),用w_{x1y1-x2y2}表示pixel(x1,y1)和pixel(x2,y2)的affinity weight(已經歸一化),則Colorization的整個線性方程組可以表示為如下(右鍵檢視大圖):
可見,其矩陣跟上述Poisson Equation中的矩陣形式一模一樣(滿足Laplacian Matrix的幾個特點,其實也可以稱之為Laplacian Matrix),只是矩陣元素的值不再是固定值,而是跟輸入有關,而且是spatially varying。注意:這裡使用的neighborhood是四鄰域,Levin的程式碼中使用的是8鄰域。
GradientShop framework的另一個特例是WLS filter [5]。令constraint image S為輸入影象本身,G=0,而lambda_1是根據輸入影象的gradient進行spatially varying weighting:某個pixel的gradient越大,lambda_1越小(期待與輸入影象較為接近);gradient越小,lambda_1越大(進行smoothing)。這樣的效果就是進行edge-preserving smoothing,在decomposition-manipulation-recombination時可以避免artifacts的產生。
最後值得一提的是,在Gradient Domain進行操作的其他work有:Diffusion Curves [9],Gradient
Domain Painting [10] 等,都是很有趣的東東。另外,沒有通過解線性方程組而是通過操作Laplacian Pyramid的local Laplacian filter [11]也是很有趣的work,個人非常喜歡,能生成類似於夢幻般的影象效果並且沒有什麼artifacts,例如下圖。

2.2 Problem II: Closed-Form Matting
Image Matting就是精確摳圖問題,主要是用來摳出毛髮等具有半透明邊界的物體,可以用以下方程描述:
給一個輸入影象I,以及部分foreground和background的標記(用Trimap或者scribbles標記,如下圖),目標是求出alpha matte, F和B。
Levin的Closed-Form Matting [4] 主要基於一個非常有見地的假設 -- Local Linear Model,大概意思就是,在一個很小的local window裡,alpha matte應當可以用影象的三個顏色通道線性表出(linear combination),即下圖所示:
這個模型的精妙之處在於:第一,將原有的composition equation中的三個未知變數alpha,F,B解耦合,變成了未知變數alpha,a,b,而三個未知變數之間不再有相乘的關係,也就是nonlinear model轉化成了linear model;第二,由於a和b是在一個local window裡不變的,而每個pixel都被好幾個重疊的local window覆蓋,這些互相重疊的local window使得使用者的輸入可以有效進行propagation。有了這個模型,可以直接對其進行Regularized Least Squares Minimization來求解alpha,即:
其中w_j是每個pixel j附近的local window,S是使用者輸入的scribbles,epsilon是regularization parameter(該regularization term相當於prior:希望alpha matte較為smooth)。該optimization中包含三個未知變數(每個pixel:alpha, a, b),但幸運的是,目標函式相對於每個未知變數都是quadratic的,因此可以推匯出其closed-form的解(分別對alpha,a,b求偏導並令式子等於0)。仔細觀察目標函式,發現其關於a和b比較簡單:每個pixelj可以單獨計算。如果先將alpha看做已知,把目標函式對a和b求偏導並令其等於0,可以很容易計算出每個pixelj處a和b的表示式(包含alpha),然後再將其代入目標函式中,可以得到一個只包含一個未知變數alpha的目標函式(仍然是quadratic),寫成矩陣形式如下(注意,這時求alpha不像剛才求a和b那麼簡單,無法對每個pixel分別求出alpha,因為每個pixel的未知量alpha與其他pixel的未知量有關聯,只能通過求解線性方程組才能求出alpha):
其中alpha是所有pixel的alpha value組成的列向量,其中L是可以由輸入影象計算出的已知矩陣,Levin稱之為Matting Laplacian Matrix,與前面介紹的Poisson Equation中的Laplacian Matrix有著很一致的形式和功能(propagation user input)。假設影象有N個pixel,Matting Laplacian是一個N×N的矩陣,其中在(i,j)處的元素為:
可以看出,只有當i和j代表的pixel處於同一個local window時,元素(i,j)才不為0。將δ_ij單獨提出來(其實只有對角線上的元素有這一項),令
Levin稱之為Matting Affinity,跟前面colorization中用到的affinity相似,只是這裡的affinity值可能為負。如果將local window size為2×2(只是為了方便直觀顯示,事實上一般用奇數邊長的window size),以5×5的影象為例,Matting Laplacian可以表示成如下形式(注意:只要兩個相鄰的pixel能放入一個2×2的window,其affinity就不為空,因此事實上每個pixel周圍8鄰域的pixel的affinity都不為空):
注意其中形如的元素表示的是輸入影象中pixel(3,3)和pixel(3,4)的affinity。由上可見,Matting Laplacian的形式與colorization中的Laplacian Matrix形式基本一致(如果colorization也用8鄰域,那麼形式一模一樣)。考慮進去目標函式的constraint(即input
scribbles),可以使用跟上面colorization類似的mask列出方程組,或者使用Levin的TPAMI文章裡介紹的方法。這裡有Levin提供的Matlab程式碼。需要注意的是:這裡的對角線元素不一定非負(non-negative),非對角線元素也不一定非正(non-positive),但是整個矩陣仍然是半正定(positive
semidefinite)(Levin的paper [4]裡有證明),當然也是對稱陣。(注意有些為前面的Laplacian Matrix特別定製的解線性方程組的演算法不一定適用於這裡的Matting
Laplacian Matrix,比如[13],針對的是非對角元素必須non-positive)。
另外值得一提的是,使用和這裡同樣的Local Linear Model,假設alpha matte是一個給定的guidance影象,將目標改成要計算出從原始影象到guidance影象的local linear transformation(即求出a和b的值),將global optimization變為local window內的optimization,可以匯出一個計算起來非常快的edge-preserving filter,這就是guided
filter [12]。該filter由於其計算速度快,可以作為經典的bilateral filter的近似,很受歡迎。
2.3 Solvers: Solving Large Sparse Linear System
解大型稀疏線性方程組是一個很well-studied的問題,一般來講,解法分為兩大類:直接法(direct solver)和迭代法(iterative solver)。直接解法一般指高斯消元法(Gaussian Elimination),比如對於普通矩陣用LU Decomposition,對於對稱正定陣用Cholesky Decomposition。這類演算法的問題是,計算的過程中稀疏矩陣會變成稠密矩陣,如果矩陣規模較大(對於影象處理來講很正常,比如對於1000×1000的影象,矩陣規模達到1000000×1000000),儲存計算過程中的稠密矩陣都是問題,這就是文獻中經常提到的fill-in問題[14]。這類方法的另一個問題是不太容易並行化。當然,也有很多新的direct演算法克服了這些問題,參見Tim Davis的大作Direct Methods for Sparse Linear Systems [15](貌似Matlab裡的backslash用的就是direct演算法)。不過在computer vision中較受歡迎的還是iterative演算法,推薦一本很棒的教科書,就是Yousef Saad的Iterative Methods for Sparse Linear Systems [16]。在ICCV 2007 gradient course中,有一個很棒的總結(section3 ppt)。這裡也有個不錯的總結。這裡有個很棒的介紹Jacobi/Gauss-Seidel/SOR的ppt。
先將上述涉及到的方程組的係數矩陣及可以使用的演算法進行一個分類,注意有些演算法是對所有矩陣通用的,有些演算法只能用於一些特定矩陣。以下分類基本是從上往下呈包含關係:
2. 對稱正定陣(symmetric positive-definite, SPD):Cholesky Decomposition,Conjugate Gradient,Hierarchical Preconditioning (ABF) [14][17];
3. M-matrix(非對角元素是non-positive的Laplacian Matrix,包括上述的Poisson Equation,colorization以及WLS filter中的Laplacian Matrix,但是不包括matting中的矩陣):Hierarchical Preconditioning (HSC)[13];
4. Spatially homogeneous Laplacian Matrix in Poisson Equation(在[13]中被如此稱呼,注意跟homogeneous Poisson Equation不同):FFT-based Poisson Solver (or see Chapter 2.2.6, Saad [16]);
這些涉及到的演算法的複雜度如下(參見這裡)(N是未知元素的個數,即影象畫素個數):
| 演算法 | 時間複雜度 | 適用矩陣型別 |
| SOR | N^(3/2) | Diagonal dominant |
| N^(3/2) | Symmetric positive-definite | |
| N^(3/2) | Symmetric positive-definite | |
| N | M-matrix (off-diagonal non-positive) |
2.4 Reference
[2] P. Perez, M. Gangnet, and A. Blake, "Poisson Image Editing," SIGGRAPH, 2003.
[3] A. Levin, D. Lischinski, and Y. Weiss, “Colorization Using Optimization,” SIGGRAPH, 2004.
[4] A. Levin, D. Lischinski, and Y. Weiss, “A Closed-Form Solution to Natural
Image Matting,” CVPR, 2006. ->TPAMI2008 extension.
[11] S. Paris, S.W. Hasinoff, J. Kautz, "Local Laplacian Filters: Edge-aware Image Processing with a Laplacian Pyramid," SIGGRAPH, 2011.
[12] K. He, J. Sun, and X. Tang, "Guided Image Filtering," ECCV, 2010. ->TPAMI 2012
extension.