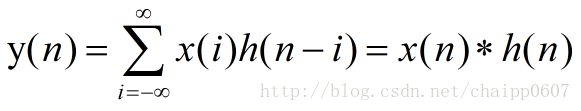影象處理中的卷積
數字訊號處理中卷積
卷積一詞最開始出現在訊號與線性系統中,訊號與線性系統中討論的就是訊號經過一個線性系統以後發生的變化。由於現實情況中常常是一個訊號前一時刻的輸出影響著這一時刻的輸出,所在一般利用系統的單位響應與系統的輸入求卷積,以求得系統的輸出訊號(當然要求這個系統是線性時不變的)。
卷積的定義:
卷積是兩個變數在某範圍內相乘後求和的結果。如果卷積的變數是序列x(n)和h(n),則卷積的結果:
數字影象處理中卷積
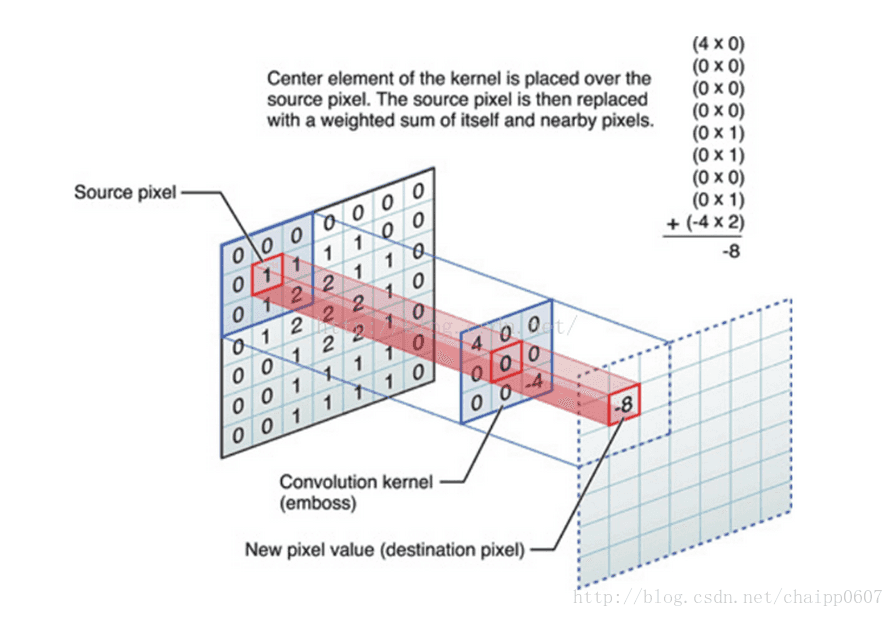
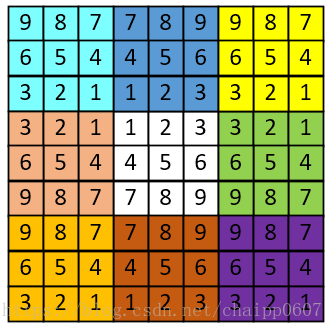
數字影象是一個二維的離散訊號,對數字影象做卷積操作其實就是利用卷積核(卷積模板)在影象上滑動,將影象點上的畫素灰度值與對應的卷積核上的數值相乘,然後將所有相乘後的值相加作為卷積核中間畫素對應的影象上畫素的灰度值,並最終滑動完所有影象的過程。
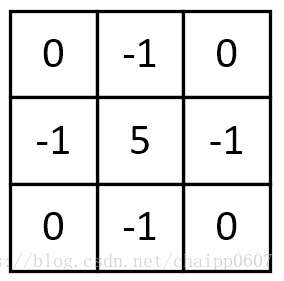
這張圖可以清晰的表徵出整個卷積過程中一次相乘後相加的結果:該圖片選用3*3的卷積核,卷積核內共有九個數值,所以圖片右上角公式中一共有九行,而每一行都是影象畫素值與卷積核上數值相乘,最終結果-8代替了原影象中對應位置處的1。這樣沿著圖片一步長為1滑動,每一個滑動後都一次相乘再相加的工作,我們就可以得到最終的輸出結果。除此之外,卷積核的選擇有一些規則:
1)卷積核的大小一般是奇數,這樣的話它是按照中間的畫素點中心對稱的,所以卷積核一般都是3x3,5x5或者7x7。有中心了,也有了半徑的稱呼,例如5x5大小的核的半徑就是2。
2)卷積核所有的元素之和一般要等於1,這是為了原始影象的能量(亮度)守恆。其實也有卷積核元素相加不為1的情況,下面就會說到。
3)如果濾波器矩陣所有元素之和大於1,那麼濾波後的影象就會比原影象更亮,反之,如果小於1,那麼得到的影象就會變暗。如果和為0,影象不會變黑,但也會非常暗。
4)對於濾波後的結構,可能會出現負數或者大於255的數值。對這種情況,我們將他們直接截斷到0和255之間即可。對於負數,也可以取絕對值。
邊界補充問題
上面的圖片說明了影象的卷積操作,但是他也反映出一個問題,如上圖,原始圖片尺寸為7*7,卷積核的大小為3*3,當卷積核沿著圖片滑動後只能滑動出一個5*5的圖片出來,這就造成了卷積後的圖片和卷積前的圖片尺寸不一致,這顯然不是我們想要的結果,所以為了避免這種情況,需要先對原始圖片做邊界填充處理。在上面的情況中,我們需要先把原始影象填充為9*9的尺寸。
常用的區域填充方法包括:
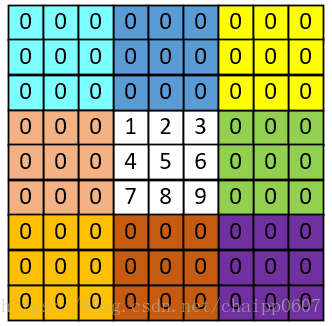
為了畫圖方便,這裡就不用5*5的尺寸了,用3*3定義原始影象的尺寸,補充為9*9的尺寸,圖片上的顏色只為方便觀看,並沒有任何其他含義。
原始影象:
補零填充
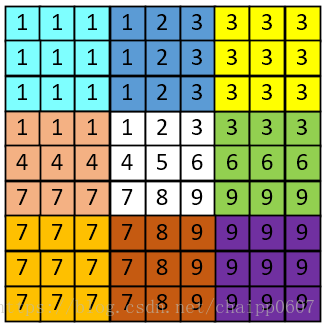
邊界複製填充
映象填充
塊填充
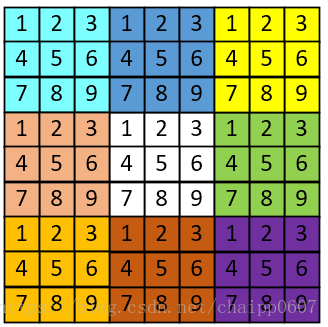
以上四種邊界補充方法通過看名字和圖片就能理解了,不在多做解釋。
不同卷積核下卷積意義
我們經常能看到的,平滑,模糊,去燥,銳化,邊緣提取等等工作,其實都可以通過卷積操作來完成,下面我們一一舉例說明一下:
一個沒有任何作用的卷積核:
卷積核:
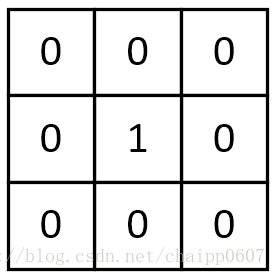
將原畫素中間畫素值乘1,其餘全部乘0,顯然畫素值不會發生任何變化。
平滑均值濾波:
選擇卷積核:

該卷積核的作用在於取九個值的平均值代替中間畫素值,所以起到的平滑的效果:

高斯平滑:
卷積核:
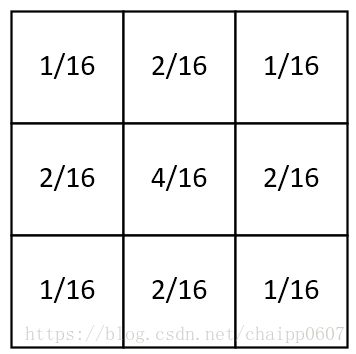
高斯平滑水平和垂直方向呈現高斯分佈,更突出了中心點在畫素平滑後的權重,相比於均值濾波而言,有著更好的平滑效果。
影象銳化:
卷積核:
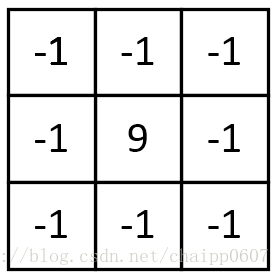
該卷積利用的其實是影象中的邊緣資訊有著比周圍畫素更高的對比度,而經過卷積之後進一步增強了這種對比度,從而使影象顯得稜角分明、畫面清晰,起到銳化影象的效果。

除了上述卷積核,邊緣銳化還可以選擇:
梯度Prewitt:
水平梯度卷積核:
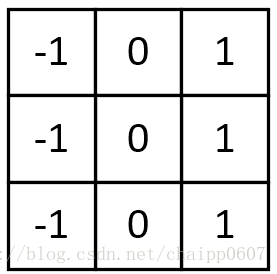

垂直梯度卷積核:
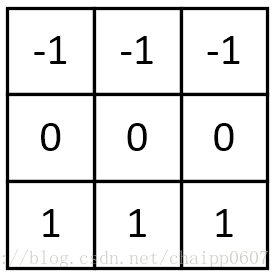
梯度Prewitt卷積核與Soble卷積核的選定是類似的,都是對水平邊緣或垂直邊緣有比較好的檢測效果。
Soble邊緣檢測:
Soble與上述卷積核不同之處在於,Soble更強調了和邊緣相鄰的畫素點對邊緣的影響。
水平梯度:
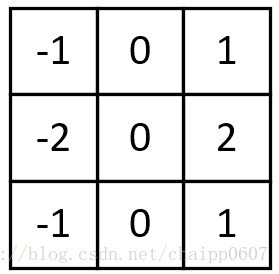

垂直梯度:
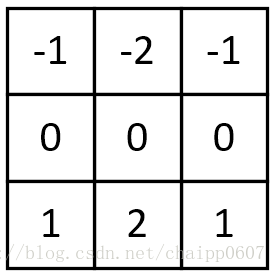
以上的水平邊緣與垂直邊緣檢測問題可以參考:Soble運算元水平和垂直方向導數問題
梯度Laplacian:
卷積核:

Laplacian也是一種銳化方法,同時也可以做邊緣檢測,而且邊緣檢測的應用中並不侷限於水平方向或垂直方向,這是Laplacian與soble的區別。下面這張圖可以很好的表徵出二者的區別:來源於OpenCV官方文件