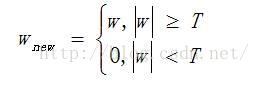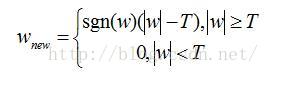轉載：http://blog.csdn.net/ebowtang/article/details/40481393

一，小波閾值去噪基本理論

1，小波閾值處理基本理論

小波閾值收縮法是Donoho和Johnstone在1995年提出的，以下便是養活不少學者的三篇基礎論文，引得無數學者在此基礎上優化，或者應用到自己的工程中然後發表相關的論文：

【1】 Donoho D L. De-noising by soft-thresholding. IEEE Trans- actions on Information Theory, 1995, 41(3): 613−627
【2】 Donoho D L, Johnstone I M. Adapting to unknown smooth- ness via wavelet shrinkage. Journal of the American Statistic
Association, 1995, 90(432): 1200−1224
【3】 Donoho D L, Johnstone I M, Kerkyacharian G, Picard D. Wavelet shrinkage: asymptopia? Journal of Royal Statisti-
cal Society Series B, 1995, 57(2): 301−369

所謂閾值去噪簡而言之就是對訊號進行分解，然後對分解後的係數進行閾值處理，最後重構得到去噪訊號。該演算法其主要理論依據是：小波變換具有很強的去資料相關性,它能夠使訊號的能量在小波域集中在一些大的小波係數中;而噪聲的能量卻分佈於整個小波域內.因此,經小波分解後,訊號的小波係數幅值要大於噪聲的係數幅值.可以認為,幅值比較大的小波係數一般以訊號為主，而幅值比較小的係數在很大程度上是噪聲.於是,採用閾值的辦法可以把訊號係數保留,而使大部分噪聲係數減小至零.小波閾值收縮法去噪的具體處理過程為:將含噪訊號在各尺度上進行小波分解,設定一個閾值，幅值低於該閾值的小波係數置為0,高於該閾值的小波係數或者完全保留,或者做相應的“收縮(shrinkage)”處理.最後將處理後獲得的小波係數用逆小波變換進行重構,得到去噪後的訊號.

2，閾值函式的選取

  小波分解閾值去噪中,閾值函式體現了對超過和低於閾值的小波係數不同處理策略，是閾值去噪中關鍵的一步。設w表示小波係數,T為給定閾值,sign(*)為符號函式,常見的閾值函式有：

硬閾值函式：     （小波係數的絕對值低於閾值的置零，高於的保留不變）

軟閾值函式：   （小波係數的絕對值低於閾值的置零，高於的係數shrinkage處理）

值得注意的是：

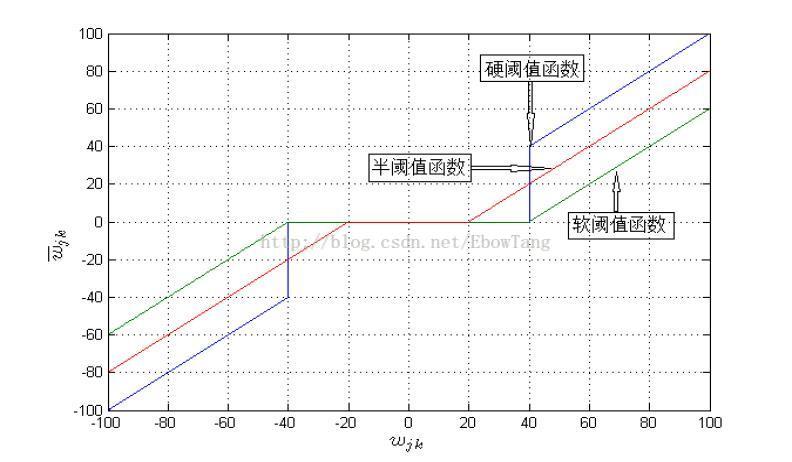
1) 硬閾值函式在閾值點是不連續的，在下圖中已經用黑線標出。不連續會帶來振鈴，偽吉布斯效應等。

2) 軟閾值函式，原係數和分解得到的小波係數總存在著恆定的偏差,這將影響重構的精度

同時這兩種函式不能表達出分解後係數的能量分佈，半閾值函式是一種簡單而經典的改進方案。見下圖：

                                                                               圖1

3，閾值的確定

選取的閾值最好剛好大於噪聲的最大水平，可以證明的是噪聲的最大限度以非常高的概率低於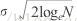（此閾值是Donoho提出的），其中根號右邊的這個引數（叫做sigma）就是估計出來的噪聲標準偏差（根據第一級分解出的小波細節係數，即整個det1絕對值係數中間位置的值），本文將用此閾值去處理各尺度上的細節係數，注意所謂全域性閾值就是近似係數不做任何閾值處理外，其他均閾值處理。

最後吐槽一下這個“絕對值係數中間位置的值”

1）如果det1的長度為偶數那麼，這個“中值”便是中間位置的兩個數之和的平均值，比如【2,2,3,5】，中值即是2.5而不是3

2）如果det1的長度為奇數那麼，這個中值就是中間位置的那個數，比如【2,3,5】，中值即3

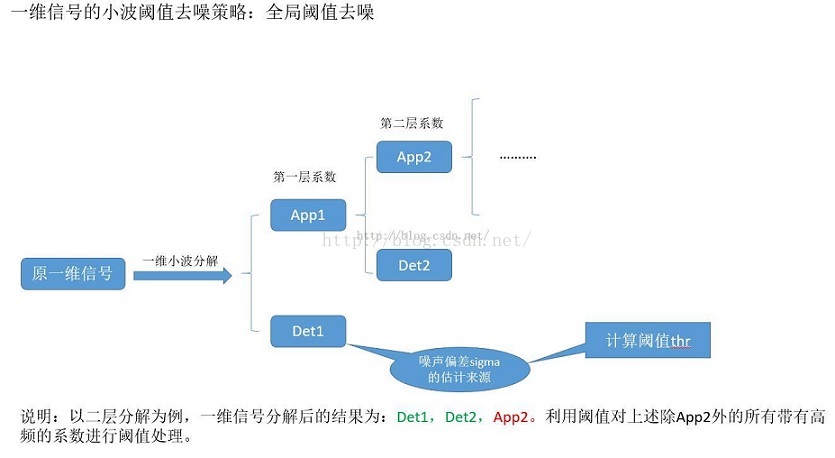
4，閾值策略

以前寫的ppt挪用過來：

5，一維訊號的多級分解與重構

二，matlab實現一維小波閾值去噪

1，核心庫函式說明

1）wnoisest函式

作用：估計一維小波高頻係數中的噪聲偏差

這個估計值使用的是絕對值中間位置的值（估計的噪聲偏差值）除以0.6745（Median Absolute Deviation / 0.6745），適合0均值的高斯白噪聲

2）wavedec函式

一維訊號的多尺度分解，將返回諸多細節係數和每個係數的長度，在matlab中鍵入“doc wavedec”具體功能一目瞭然

3）waverec函式

一維訊號小波分解係數的重構，將返回重構後的訊號在matlab中鍵入“doc waverec”具體功能一目瞭然，也可以鍵入“open waverec”檢視matlab具體是怎麼做的。

4）wdencmp函式

這個函式用於對一維或二維訊號的壓縮或者去噪，使用方法：
1 [XC,CXC,LXC,PERF0,PERFL2] = wdencmp('gbl',X,'wname',N,THR,SORH,KEEPAPP) 
2 [XC,CXC,LXC,PERF0,PERFL2] = wdencmp('lvd',X,'wname',N,THR,SORH) 
3 [XC,CXC,LXC,PERF0,PERFL2] = wdencmp('lvd',C,L,'wname',N,THR,SORH) 
wname是所用的小波函式，

gbl(global的縮寫)表示每層都採用同一個閾值進行處理，

lvd表示每層用不同的閾值進行處理，

N表示小波分解的層數，

THR為閾值向量，

對於格式(2)(3)每層都要求有一個閾值，因此閾值向量THR的長度為N，

SORH表示選擇軟閾值還是硬閾值(分別取為’s’和’h’)，

引數KEEPAPP取值為1時，則低頻係數不進行閾值量化處理，反之，則低頻係數進行閾值量化。

XC是消噪或壓縮後的訊號，[CXC，LXC]是XC的小波分解結構，

PERF0和PERFL2是恢復和壓縮L^2的範數百分比, 是用百分制表明降噪或壓縮所保留的能量成分。

1. clc;  
2. clear;  
3. % 獲取噪聲訊號  
4. load leleccum;  
5. indx = 1:3450;  
6. noisez = leleccum(indx);  
7. %訊號的分解  
8. wname = 'db3';   
9. lev = 3;  
10. [c,l] = wavedec(noisez,lev,wname);  
11. %求取閾值  
12. sigma = wnoisest(c,l,1);%使用庫函式wnoisest提取第一層的細節係數來估算噪聲的標準偏差  
13. N = numel(noisez);%整個訊號的長度  
14. thr = sigma*sqrt(2*log(N));%最終閾值  
15. %全域性閾值處理  
16. keepapp = 1;%近似係數不作處理  
17. denoisexs = wdencmp('gbl',c,l,wname,lev,thr,'s',keepapp);  
18. denoisexh = wdencmp('gbl',c,l,wname,lev,thr,'h',keepapp);  
19. % 作圖  
20. subplot(311),   
21. plot(noisez), title('原始噪聲訊號');  
22. subplot(312),  
23. plot(denoisexs), title('matlab軟閾值去噪訊號') ;  
24. subplot(313),  
25. plot(denoisexh), title('matlab硬閾值去噪訊號') ;