題目在伯樂線上中看到的，據說是twitter面試時的題目，感覺蠻有意思的。於是就將兩種演算法都用C++實現了，就當練練手吧。

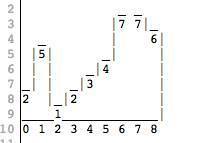
        “在這個圖片裡我們有不同高度的牆。這個圖片由一個整數陣列所代表，陣列中每個數是牆的高度。上邊的圖可以表示為陣列[2,5,1,2,3,4,7,7,6]”

       “假如開始下雨了，那麼牆之間的水坑能夠裝多少水呢？”

     “以1×1的方塊為單位計算容積。所以，在上邊的圖中下標為1以左的都會漏掉。下標7以右的也會漏掉。剩下的只有在1和6之間的一坑水，容積是10”

        作者已經給出了兩種演算法，邏輯如下：

        兩次遍歷的演算法：

        如果我們從左至右遍歷列表，每個下標水的量最多是到現在為止最大的數。這表示如果我們已知右邊有相等或更大的，我們可以知道存下的水有多少。反向遍歷的時候也一樣：如果我們知道左邊有比右邊最大的數更大的，我們裝水是毫無問題的。

        基於這個想法，一個解決方法是：先找到最大值，從左遍歷到最大值，然後從右遍歷到最大值。這個方法需要兩次遍歷：一次找到最大值，另一次分成了兩個子遍歷。

        一次遍歷的演算法：

        一次遍歷的方法通過兩端的指標相向移動避免了尋找最大值。如果（左指標找到的左指標以左的最大值）小於（右指標找到右指標以右的最大值），將左指標向右移動一位。否則右指標向左移動一位。重複過程直到兩個指標相遇。（解釋起來很麻煩，但是程式碼很簡單）

        兩次遍歷：

/************************************************************************/
/* 兩次遍歷的方法                                                                     */
/************************************************************************/
int calculateVolume(int arrays[],int length){
	
	//先求出陣列中的最大值，第一次遍歷
	int max=0;//最大值
	int max_pos;//最大值對於陣列的下標
	for (int i=0;i<length;i++)
	{
		if (max<arrays[i])
		{
			max=arrays[i];
			max_pos=i;
		}
	}

	int max_left=0;//從左邊開始遍歷時的極大值
	int max_right=0;//從右邊開始遍歷時的極大值
	int volume=0;//容積

	//從左邊開始向右遍歷到最大值處
	for(int i=0;i<max_pos;i++){
		//不斷更新左邊的極大值
		if (max_left<arrays[i])
		{
			max_left=arrays[i];
		}
		//否則，加上新增加的容積
		else{
			volume+=(max_left-arrays[i]);
		}
	}

	//從最右邊開始向左遍歷到最大值處
	for(int j=length-1;j>max_pos;j--){
		//不斷更新右邊的極大值
		if (max_right<arrays[j])
		{
			max_right=arrays[j];
		}
		//否則，加上新增加的容積
		else{
			volume+=(max_right-arrays[j]);
		}
	}
	
	return volume;
}
 

void main(){
	int arrays1[]={2,5,1,2,3,4,7,7,6};
	int arrays2[]={2,5,1,3,1,2,1,7,7,6};
	int arrays3[]={6,1,4,6,7,5,1,6,4};
	std::cout<<"arrays1 voleme: "<<calculateVolume(arrays1,9)<<std::endl;
	std::cout<<"arrays2 voleme: "<<calculateVolume(arrays2,10)<<std::endl;
	std::cout<<"arrays3 voleme: "<<calculateVolume(arrays3,9)<<std::endl;
}

        一次遍歷的演算法：

/************************************************************************/
/* 一次遍歷的方法                                                                     */
/************************************************************************/
int calculateVolumeEx(int  arrays[],int length){
	int pos_left=0;//從左開始遍歷的指標的下標
	int pos_right=length-1;//從右開始遍歷的指標的下標
	int max_left=arrays[pos_left];//從左開始遍歷的過程中的極大值
	int max_right=arrays[pos_right];//從右開始遍歷的過程中的極大值
	int volume=0;//儲存容積的變數

	//當右邊的指標的下標大於座標指標的下標時，重複迴圈
	//迴圈調出時即遍歷完了陣列中的所有元素
	while(pos_right>pos_left){

		//如果左指標找到的極大值小於右指標找到的極大值，左指標右移
		if (max_left<max_right)
		{
			pos_left=pos_left+1;

			//當左指標指向的新的元素大於之前找到的極大值時，用新的值替換極大值
			if (arrays[pos_left]>=max_left)
			{
				max_left=arrays[pos_left];
			}
			//否則總容積加上新的容積
			else{
				volume+=(max_left-arrays[pos_left]);
			}
		}
		//如果左指標找打的極大值大於或等於右指標找到的極大值，右指標左移
		else{
			pos_right=pos_right-1;
			int tmp_right=arrays[pos_right];//儲存右指標指向的臨時變數

			//當右指標指向的新的元素大於之前找到的極大值時，用新的值替換極大值
			if (arrays[pos_right]>=max_right)
			{
				max_right=arrays[pos_right];
			}
			//否則總容積加上新的容積
			else{
				volume+=(max_right-arrays[pos_right]);
			}
		}
	}

	return volume;

}

void main(){
	int arrays1[]={2,5,1,2,3,4,7,7,6};
	int arrays2[]={2,5,1,3,1,2,1,7,7,6};
	int arrays3[]={6,1,4,6,7,5,1,6,4};
	std::cout<<"arrays1 voleme: "<<calculateVolumeEx(arrays1,9)<<std::endl;
	std::cout<<"arrays2 voleme: "<<calculateVolumeEx(arrays2,10)<<std::endl;
	std::cout<<"arrays3 voleme: "<<calculateVolumeEx(arrays3,9)<<std::endl;
}