Java資料結構與演算法解析(九)——B樹
阿新 • • 發佈:2019-02-05
B樹簡介
定義
在電腦科學中,B樹(英語:B-tree)是一種自平衡的樹,能夠保持資料有序。這種資料結構能夠讓查詢資料、順序訪問、插入資料及刪除的動作,都在對數時間內完成。
特點
階為M的B樹是一顆具有以下特點的樹:
1.資料項儲存在樹葉上
2.非葉子節點直到M-1個關鍵字以指示搜尋的方向:關鍵字i代表子樹i+1中最小的關鍵字
3.樹的根或者是一片樹葉,或者其兒子在2和M之間
4.除根外,所有非樹葉節點的兒子數在M/2和M之間。
5.所有的樹葉都在相同的深度上並有L/2和L之間個數據項
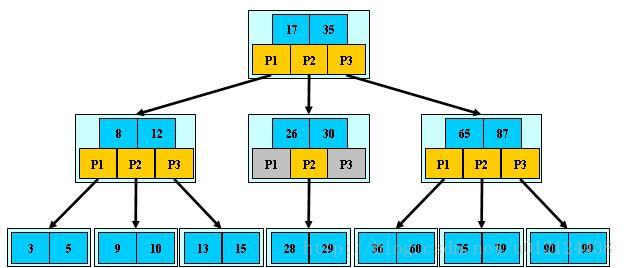
例如:(M=3)
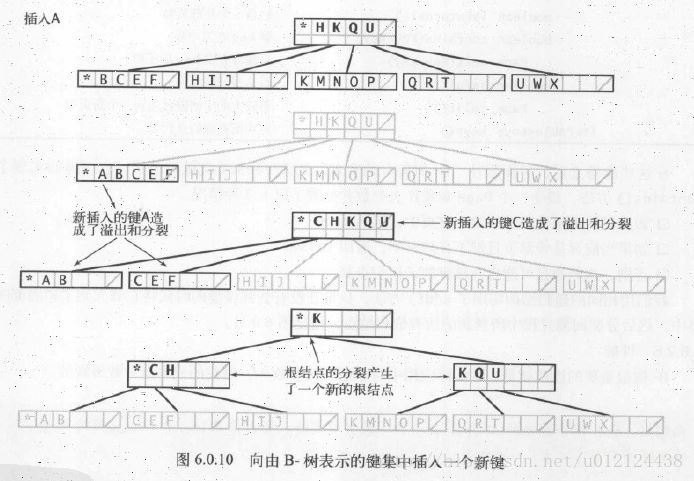
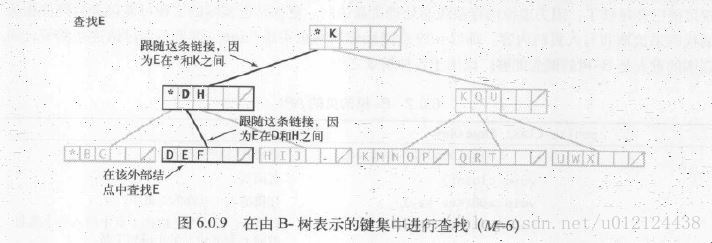
查詢和插入
為了方便這裡用了一個特殊的哨兵鍵,它小於其他所有鍵,用*表示。
一開始B樹只含有一個根結點,而根結點在初始化時僅含有該哨兵鍵。
內部結點中的每個鍵都與一個結點相關聯,以此結點為根的子樹種,所有的鍵都大於等於與此結點關聯的鍵,但小於其他所有鍵。
B樹的實現
public class BTree2<K, V>
{
private static Log logger = LogFactory.getLog(BTree.class);
/**
* B樹節點中的鍵值對。
* <p/>
* B樹的節點中儲存的是鍵值對。
* 通過鍵訪問值。
*
* @param