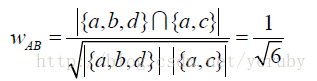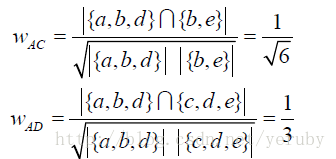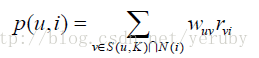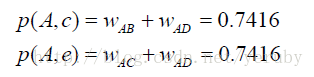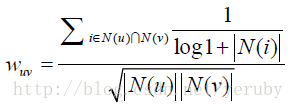UserCF：UserCollaborationFilter，基於使用者的協同過濾

演算法核心思想：在一個線上推薦系統中，當用戶A需要個性化推薦時，可以先找到和他有相似興趣的其它使用者，然後把那些使用者喜歡的、而使用者A沒有聽說過的物品推薦給A，這種方法稱為基於使用者的協同過濾演算法。

==>可以看出，這個演算法主要包括兩步：

一、找到和目標使用者興趣相似的使用者集合——計算兩個使用者的興趣相似度

二、找到這個集合中的使用者喜歡的，且目標使用者沒有聽說過的物品推薦給目標使用者——找出物品推薦

下面分別來看如何實現這兩步：

一、計算兩個使用者的興趣相似度：

給定使用者u和使用者v，令N(u)表示使用者u感興趣的物品集合，N(v)表示使用者v感興趣的物品集合，那麼可以通過Jaccard公式或者通過餘弦相似度公式計算：

...Jaccard公式

...餘弦相似度公式

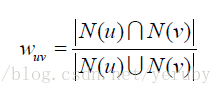
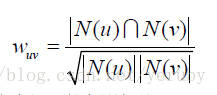
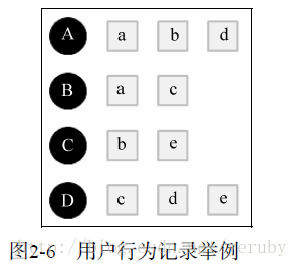
舉例：下圖表示使用者A對物品{a,b,d}有過行為，使用者B對物品{a,c}有過行為

利用餘弦相似度計算可得：

使用者A和使用者B的興趣相似度為：

同理，

但是，需要注意的是，這種方法的時間複雜度是O(U^2)，因為我們需要計算每一對使用者之間的相似度，事實上，很多使用者相互之間並沒有對同樣的物品產生過行為，所以很多時候當分子為0的時候沒有必要再去計算分母，所以這裡可以優化：即首先計算出|N(u) 並 N(v)| != 0 的使用者對(u,v)，然後對這種情況計算分母以得到兩個使用者的相似度。

針對此優化，需要2步：

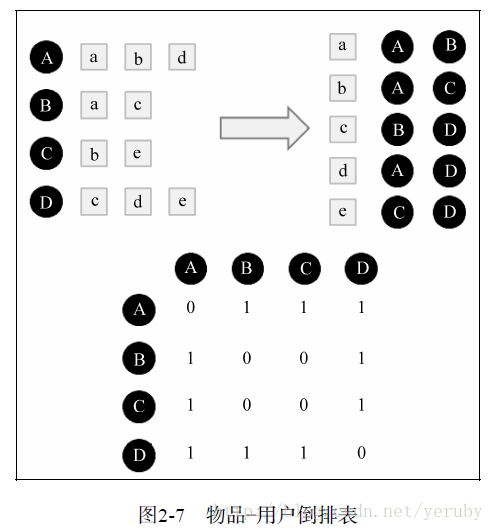
（1）建立物品到使用者的倒查表T，表示該物品被哪些使用者產生過行為；

（2）根據倒查表T，建立使用者相似度矩陣W：在T中，對於每一個物品i，設其對應的使用者為j,k，在W中，更新相應的元素值，w[j][k]=w[j][k]+1，w[k][j]=w[k][j]+1，以此類推，掃描完倒查表T中的所有物品後，就可以得到最終的使用者相似度矩陣W，這裡的W是餘弦相似度中的分子部分，然後將W除以分母可以得到最終的使用者興趣相似度。

得到使用者相似度後，就可以進行第二步了。

二、給使用者推薦和他興趣最相似的K個使用者喜歡的物品。

公式如下：

其中，p(u,i)表示使用者u對物品i的感興趣程度，S(u,k)表示和使用者u興趣最接近的K個使用者，N(i)表示對物品i有過行為的使用者集合，Wuv表示使用者u和使用者v的興趣相似度，Rvi表示使用者v對物品i的興趣（這裡簡化，所有的Rvi都等於1）。

根據UserCF演算法，可以算出，使用者A對物品c、e的興趣是：

以上就是UserCF最簡單的實現方法。

我們還可以在此基礎上進行改進，改進思想是：兩個使用者對冷門物品採取過同樣的行為更能說明他們興趣的相似度。

比如，兩個使用者都買過《新華詞典》並不能說明兩個人的興趣相似，而如果兩個人都買過《資料探勘導論》則可以認為他們的興趣相似。

==>公式如下：

可以看到，如果一個物品被大多數人有過行為，則這樣的資訊參考價值不大，權重變小。