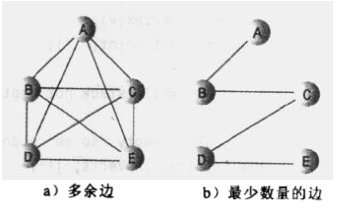
最小生成樹（MST Minimum Spanning Tree）：用最少的邊連線了所有的頂點。

最小生成樹邊的數量總比頂點V的數量小1.
即 E = V -1；

建立最小生成樹的演算法與搜尋演算法幾乎是相同的。它同樣可以基於廣度優先搜尋或者深度優先搜尋，本例使用深度優先搜尋。
在執行深度優先搜尋的過程中，記錄走過的邊，就可以建立一棵最小生成樹。最下生成樹演算法與前面的深度優先搜尋之間唯一的區別是mst()方法必須記錄走過的邊。

——————————
最小生成樹完整程式碼：

class  StackX
{
    private  final int SIZE = 20
 
;
    private int[]  st;
    private  int  top;
    //...........................
    public StackX()
    {
        st = new int[SIZE];
        top = -1;
    }
    //............................
    public  void push(int j)
    {
        st[++top] = j;
    }
    //.................
    public  int  pop()
    {
        return
 
  st[top--];
    }
    //........................
    public  int  peek()
    {
        return  st[top];
    }
    //.......................
    public  boolean  isEmpty()
    {
        return  (top == -1);
    }   
}

//....................................
class   Vertex
{
    public  char  label ;
    public
 
  boolean  wasVisited ;
    //..........................
    public  Vertex(char  lab)
    {
        label = lab;
        wasVisited  = false;
    }
}


//............................................
class  Graph
{

     private  final  int  MAX_VERTS = 20;
     private  Vertex  vertexList[]  ;
     private  int  adjMat[][];
     private  int  nVerts;  
     private  StackX  theStack;
     //.......................................
     public  Graph()
     {
         vertexList  = new  Vertex[MAX_VERTS];

         adjMat = new  int[MAX_VERTS][MAX_VERTS];
         nVerts = 0;
         for (int i = 0; i < MAX_VERTS; i++)
        for (int j = 0; j < MAX_VERTS; j++)
        adjMat[i][j] = 0;
         theStack = new StackX();
     }

     //........................
     public  void  addVertex(char  lab)
     {
         vertexList[nVerts++]  = new Vertex(lab);
     }
     //..............................

     public   void  addEdge(int start,int  end)
     {
         adjMat[start][end]  =  1;
         adjMat[end][start]  =  1;
     }

     //.............................
     public  void  displayVertex(int  v)
     {
         System.out.print(vertexList[v].label);
     }


     //..............................
     public   void  mst()
        {   //begin  at vertex  0
            vertexList[0].wasVisited = true;  //mark  it
            theStack.push(0);   //  push  it

            while(!theStack.isEmpty())   //棧不為空時
            {
                int  currentVertex  = theStack.peek();
                int  v = getAdjUnvisitedVertex(currentVertex);
                if(v == -1)
                    theStack.pop();
                else
                {
                    vertexList[v].wasVisited = true;
                    theStack.push(v);
                    displayVertex(currentVertex);;
                    displayVertex(v);
                    System.out.println(" ");
                }

            }

            for (int i = 0; i < nVerts; i++)

                vertexList[i].wasVisited = false;

        }
     //..........................


     public  int  getAdjUnvisitedVertex(int  v)
     {
         for (int i = 0; i < nVerts; i++)

            if(adjMat[v][i] ==1  &&  vertexList[i].wasVisited == false)
            return   i;
         return -1;

     }
}

//////////////////////////////////////////////////////
class  MSTApp
{
    public static void main(String[] args)
    {
        Graph  theGraph  = new  Graph();
        theGraph.addVertex('A');
        theGraph.addVertex('B');
        theGraph.addVertex('C');
        theGraph.addVertex('D');
        theGraph.addVertex('E');

        theGraph.addEdge(0,1);
        theGraph.addEdge(0,2);
        theGraph.addEdge(0,3);
        theGraph.addEdge(0,4);
        theGraph.addEdge(1,2);
        theGraph.addEdge(1,3);
        theGraph.addEdge(1,4);
        theGraph.addEdge(2,3);
        theGraph.addEdge(2,4);
        theGraph.addEdge(3,4);

        System.out.print("Minimu  spanning  tree");
         theGraph.mst();
         System.out.println();
    }
}