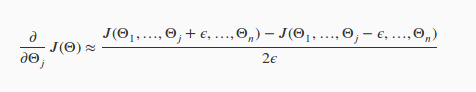代價函式和反向傳播

代價函式

首先引入一些新的我們即將討論的變數名稱：

• L = 網路的總層數
• sj$s_j$ = 網路第 j 層的單元節點數（不包含偏置項）
• K = 最後一層輸出的單元數
• m = 樣本的個數

在神經網路中，我們可能有很多輸出節點，我用 hθ(x)k$h_{\theta }(x)k_{}$ 表示 kth$k^{th}$ 的輸出。邏輯迴歸中，我們只有一個輸出 y，因此 K = 1，回顧正則化邏輯迴歸的代價函式：

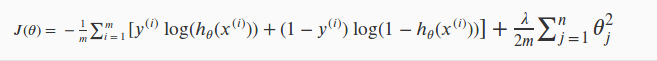
對於神經網路而言，我們的輸出一般會大於等於2個節點，因此它的代價函式會比較複雜，如下表示：

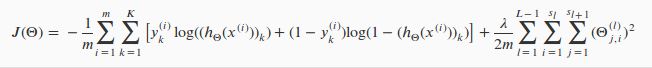
這個看起來複雜很多的代價函式背後的思想還是一樣的，方程的第一部分，在方括號之前，我們有一個巢狀求和，主要是將輸出層的每個單元的邏輯迴歸代價都加起來；正則化部分，除了

θ0${\theta }_0$ 外，將每一層的每一項 θ$\theta$ 平方再相加。
總結：

• 雙重總和只是將輸出層中每個單元計算的邏輯迴歸成本相加
• 三重總和只是將整個網路中所有單個Θ的平方加起來。

反向傳播演算法

反向傳播演算法（BP）是神經網路中用來最小化我們的代價函式的一個術語，跟我們前面講邏輯線性迴歸模型用梯度下降的方法一樣，最終的目的都是：miniθ${\theta }_{}$J(θ$\theta$)，求它的極值一樣通過求它的偏導：
，對於神經網路來說，因為這是一個複雜的模型，不能直接用公式來計算，而是採用 BP 演算法來獲得，視訊中會出現如下一張ppt，

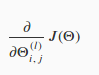
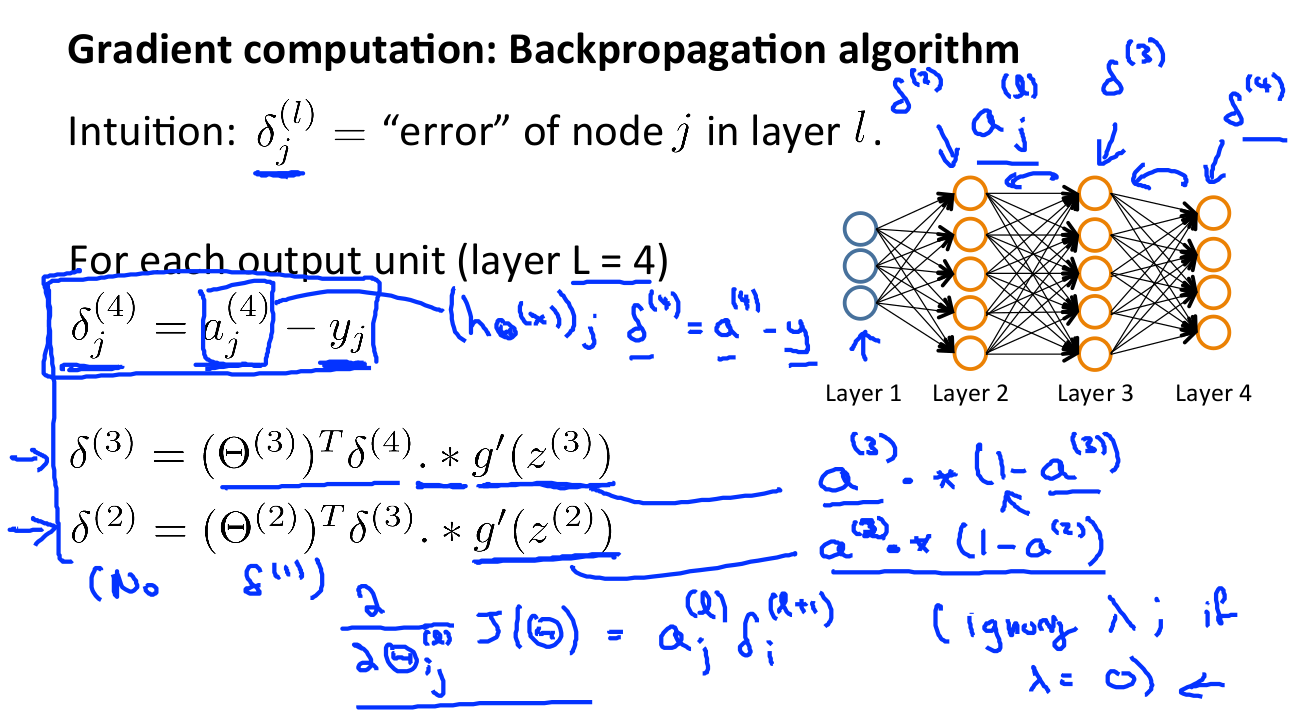
上面的幾個公式還是比較難理解的，不過不要急，仔細閱讀：https://www.zhihu.com/question/24827633/answer/91489990

，閱讀後，你應該能明白這些公式的來龍去脈。
BP演算法流程如下：

更詳細的流程：

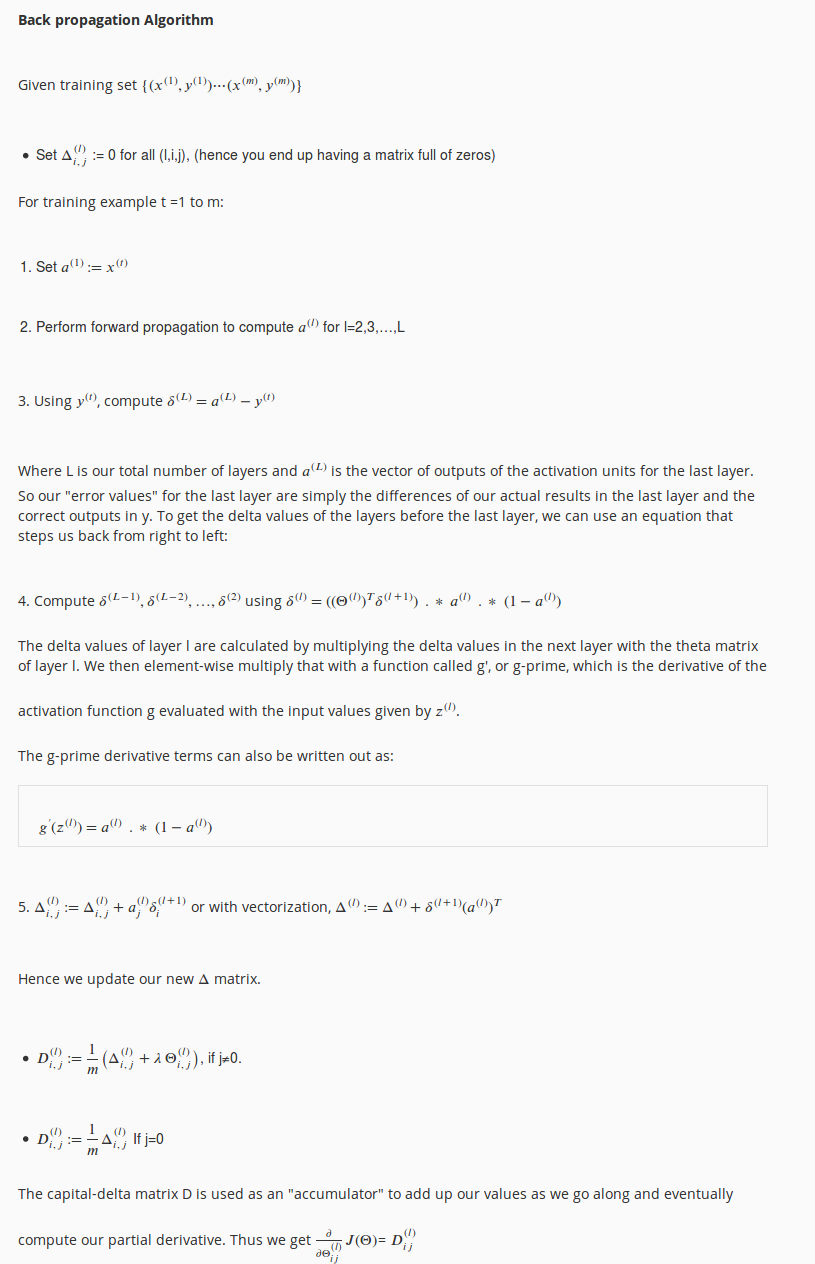
另外這裡可以參考：
【1】A Step by Step Backpropagation Example
【2】Unsupervised Feature Learning and Deep Learning Tutorial
尤其是2，建議閱讀下，會幫助你理解 BP 演算法。

反向傳播演算法的直觀理解

梯度檢驗

梯度檢驗會確保我們的BP演算法是正常工作的，因為我們對一個複雜模型做梯度下降時，難免存在一些比較難沒有發現的bug，導致梯度下降失效，等會過頭來發現bug時，時間白白浪費了，為了避免這個問題，我們可以採用一種 Numerical Gradient Checking 的方法來檢驗我們計算的偏導數是否是正確的。
對梯度的估計採用的方法是在代價函式上沿著切線的方向選擇離兩個非常近的點然後計算兩個點的平均值用以估計梯度。即對於某個特定的

θ$\theta$，我們計算出在 θ$\theta$-ϵ$ϵ$ 處和 θ$\theta$+ϵ$ϵ$ 的代價值（ϵ$ϵ$ 是一個非常小的值，通常選取 0.001），然後求兩個代價的平均，用以估計在 θ$\theta$ 處的代價值。

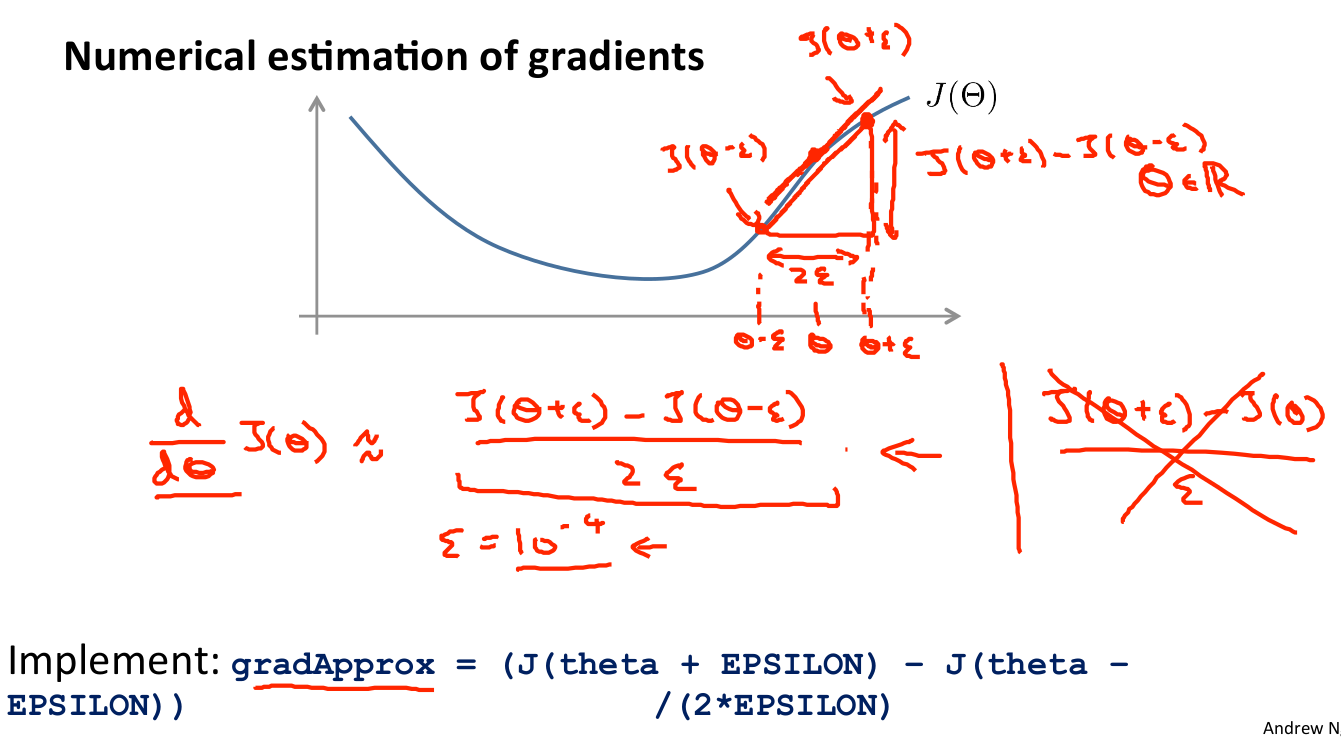
如果 θ$\theta$ 是個向量時，則用如下公式計算，這個公式不難理解。

隨機初始化

任何優化演算法都需要一些初始的引數。到目前為止我們都是初始所有引數為0，這樣的初始方法對於邏輯迴歸來說是可行的，但是對於神經網路來說是不可行的。如果我們令所有的初始引數都為0，這將意味著我們第二層的所有啟用單元都會有相同的值。同理，如果我們初始所有的引數都為一個非0的數，結果也是一樣的。

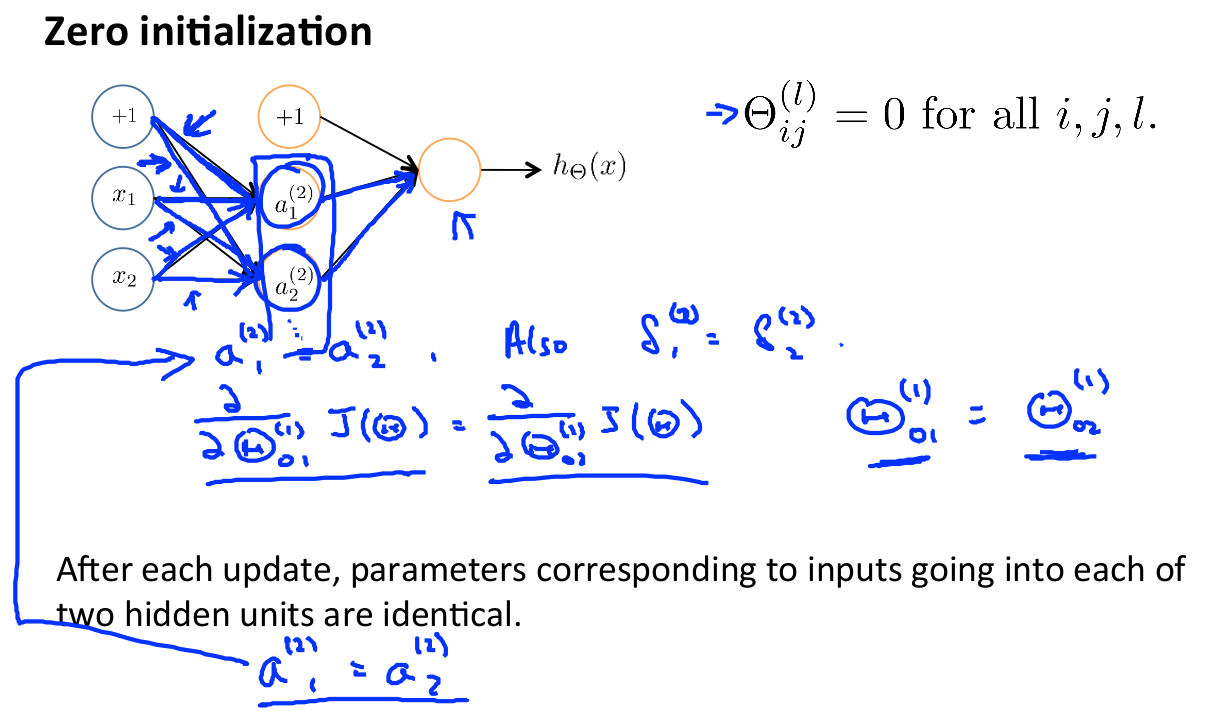
這種線性叫對稱現象，我們要打破對稱，一般是採用隨機初始化權重引數 θ$\theta$, 通常初始引數為正負ε之間的隨機值，假設我們要隨機初始一個尺寸為10×11的引數矩陣，程式碼如下：
Theta1 = rand(10, 11) * (2*eps) – eps

總結

小結一下使用神經網路時的步驟：

網路結構：第一件要做的事是選擇網路結構，即決定選擇多少層以及決定每層分別有多少個單元。

第一層的單元數即我們訓練集的特徵數量。

最後一層的單元數是我們訓練集的結果的類的數量。

如果隱藏層數大於1，確保每個隱藏層的單元個數相同，通常情況下隱藏層單元的個數越多越好。

我們真正要決定的是隱藏層的層數和每個中間層的單元數。

訓練神經網路：

1. 引數的隨機初始化
2. 利用正向傳播方法計算所有的
3. 編寫計算代價函式 的程式碼
4. 利用反向傳播方法計算所有偏導數
5. 利用數值檢驗方法檢驗這些偏導數
6. 使用優化演算法來最小化代價函式