Coursera NG 機器學習 第五週 正則化 bias Vs variance Python實現
阿新 • • 發佈:2019-01-01
ex5.py
import scipy.optimize as op import numpy as np from scipy.io import loadmat from ex5modules import * #Part 1: Loading and visualize data data=loadmat('ex5data1.mat') X=data['X'] y=data['y'] Xtest=data['Xtest'] ytest=data['ytest'] Xval=data['Xval'] yval=data['yval'] plotData(X,y) #Part 2: Costs and gradients Xone=np.column_stack((np.ones((X.shape[0],1)),X)) theta_t=np.array([1,1]).flatten() cost=lrCostFunc(theta_t,Xone,y,1) grad=lrgradient(theta_t,Xone,y,1) print("Cost at theta_t=[1,1] with lambda=1: %f (should be about 303.993)"%cost) print("Gradient at theta_t=[1,1] with lambda=1: [%f,%f] (should be about [-15.30,598.250])"%(grad[0],grad[1])) #Part 3: Train Linear Regression init_theta=np.zeros(Xone.shape[1]) lamda=0 theta=op.fmin_cg(f=lrCostFunc,x0=init_theta,args=(Xone,y,lamda),\ fprime=lrgradient,disp=False).reshape((Xone.shape[1],1)) plotLinearRegression(X,y,theta) #Part 4: Learning curve for Linear Regression train_error,val_error=learningCurve(X,y,Xval,yval,init_theta,lamda) plotLearningCurve(train_error,val_error) #Part 5: Feature Mapping for Polynomial Regression p=8 X_poly=polyFeatures(X,p) X_poly,mu,sigma=featureNormalize(X_poly) X_poly_one=np.column_stack((np.ones((X_poly.shape[0],1)),X_poly)) X_poly_test=polyFeatures(Xtest,p) X_poly_test=(X_poly_test-mu)/sigma X_poly_test_one=np.column_stack((np.ones((X_poly_test.shape[0],1)),X_poly_test)) X_poly_val=polyFeatures(Xval,p) X_poly_val=(X_poly_val-mu)/sigma X_poly_val_one=np.column_stack((np.ones((X_poly_val.shape[0],1)),X_poly_val)) lamda=3 poly_init_theta=np.zeros(X_poly_one.shape[1]) theta=op.fmin_cg(f=lrCostFunc,x0=poly_init_theta,args=(X_poly_one,y,lamda),\ fprime=lrgradient,disp=False,maxiter=200).reshape((X_poly_one.shape[1],1)) plotPolyRegression(X,y,mu,sigma,theta,p) #Part 6: Learning curve for Polynomial Regression train_error,val_error=learningCurve(X_poly,y,X_poly_val,yval,poly_init_theta,lamda) plotLearningCurve(train_error,val_error) #Part 7: Validation for Selecting Lambda lamda_vec,train_error,val_error=validationCurve(X_poly_one, y, X_poly_val_one, yval,poly_init_theta) plotLambdaError(lamda_vec,train_error,val_error) print("\nlambda\t\tTrain Error\tValidation Error") for i in range(lamda_vec.shape[0]): print(' %f\t%f\t%f'%(lamda_vec[i], train_error[i], val_error[i])) #Part 8: Testing error with best lambda=3 lamda=3 theta=op.fmin_cg(f=lrCostFunc,x0=poly_init_theta,args=(X_poly_one,y,lamda),fprime=lrgradient,disp=False,maxiter=200) test_error=lrCostFunc(theta,X_poly_test_one,ytest,0) print("Test error with lambda=3: %f (should be about 3.8599)" % test_error)
ex5modules.py
import scipy.optimize as op import numpy as np import matplotlib.pyplot as plt def sigmoid(x): return 1/(1+np.exp(-x)) def lrCostFunc(theta,X,y,lamda): m = X.shape[0] theta = theta.reshape((theta.shape[0], 1)) J=np.sum(np.square(np.dot(X,theta)-y))/(2*m)+ \ lamda*np.sum(np.square(theta[1:]))/(2*m) return J def lrgradient(theta,X,y,lamda): m = X.shape[0] theta = theta.reshape((theta.shape[0], 1)) grad=np.dot(X.T, X.dot(theta) - y) / m + theta * lamda / m grad[0] = grad[0] - theta[0] * lamda / m return grad.flatten() def learningCurve(X,y,Xval,yval,init_theta,lamda): train_error=np.zeros(X.shape[0]) val_error=np.zeros(X.shape[0]) X=np.column_stack((np.ones((X.shape[0],1)),X)) for i in range(X.shape[0]): results = op.fmin_cg(f=lrCostFunc, x0=init_theta, disp=False,\ args=(X[:i+1,:], y[:i+1,:],lamda), fprime=lrgradient,maxiter=400) theta = results.reshape((X.shape[1], 1)) train_error[i]=lrCostFunc(theta,X[:i+1,:],y[:i+1,:],lamda) val_error[i]=lrCostFunc(theta,np.column_stack((np.ones(Xval.shape[0]),Xval)),yval,lamda) return train_error,val_error def validationCurve(X, y, Xval, yval,init_theta): lamda_vec=np.array([0,0.001,0.003,0.01,0.03,.1,.3,1,3,10]) train_error=np.zeros((lamda_vec.shape[0],1)) val_error = np.zeros((lamda_vec.shape[0],1)) i=-1 for lamda in lamda_vec: i=i+1 theta=op.fmin_cg(f=lrCostFunc,x0=init_theta,disp=False,\ args=(X,y,lamda),fprime=lrgradient,maxiter=200) train_error[i]=lrCostFunc(theta,X,y,0) val_error[i]=lrCostFunc(theta,Xval,yval,0) return lamda_vec,train_error,val_error def polyFeatures(X,p): X_p = np.zeros((X.shape[0], p)) for i in range(p): X_p[:, i] = np.power(X.flatten(), i + 1) return X_p def featureNormalize(X): mu=np.mean(X,axis=0) sigma=np.std(X,axis=0,ddof=1) X_norm = (X - mu) / sigma return X_norm,mu,sigma def plotData(X,y): plt.plot(X, y, 'rx') plt.xlabel('Change in water level (x)') plt.ylabel('Water flowing out of the dam (y)') plt.show() def plotLinearRegression(X,y,theta): Xone=np.column_stack((np.ones((X.shape[0],1)),X)) plt.plot(X, y, 'rx') plt.plot(X, Xone.dot(theta), 'b') plt.xlabel('Change in water level (x)') plt.ylabel('Water flowing out of the dam (y)') plt.show() def plotLearningCurve(train_error,val_error): l1, = plt.plot(np.arange(1, 13), train_error, 'b', label='train') l2, = plt.plot(np.arange(1, 13), val_error, 'g', label='cv') plt.ylim(0, 150) plt.legend(handles=[l1, l2], loc=1) plt.title("Learning curve for linear regression") plt.xlabel("Number of training examples") plt.ylabel("Error") plt.show() def plotPolyRegression(X,y,mu,sigma,theta,p): plt.plot(X, y, 'rx') xmin = np.min(X) - 15 xmax = np.max(X) + 25 x = np.arange(xmin, xmax, .05) x_poly = polyFeatures(x, p) x_poly = (x_poly - mu) / sigma x_poly = np.column_stack((np.ones((x_poly.shape[0], 1)), x_poly)) plt.plot(x, x_poly.dot(theta), '--b') plt.xlabel('Change in water level (x)') plt.ylabel('Water flowing out of the dam (y)') plt.xlim(-80, 80) plt.ylim(np.min(x_poly.dot(theta))-10,np.max(x_poly.dot(theta)+20)) plt.show() def plotLambdaError(lamda_vec,train_error,val_error): l1,=plt.plot(lamda_vec,train_error,'b',label='Train') l2,=plt.plot(lamda_vec,val_error,'g',label='Cross Validation') plt.legend(handles=[l1,l2],loc=1) plt.xlabel("Lambda") plt.ylabel("Error") plt.xlim(0,10) plt.ylim(0,25) plt.show()
測試損失函式和梯度函式是否正確。 ![]()
線性迴歸:

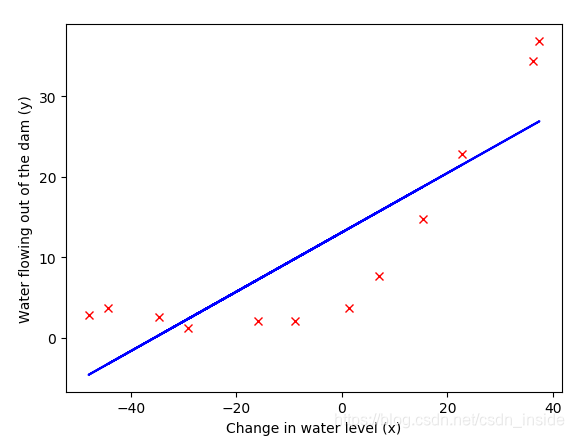
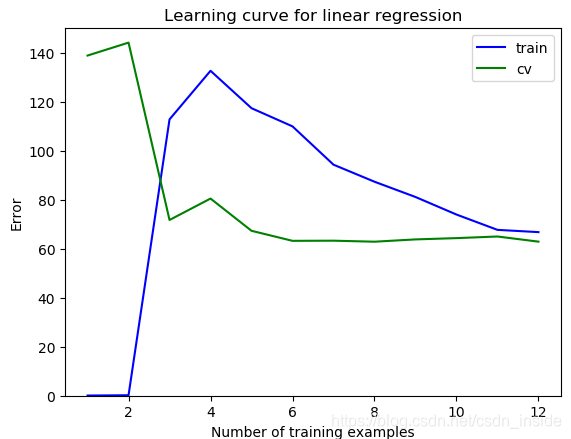
學習曲線:當lambda=0,不使用正則化時,隨著訓練集的增多,train error增加,而且值不小,cv error也不小,存在high bias的問題。

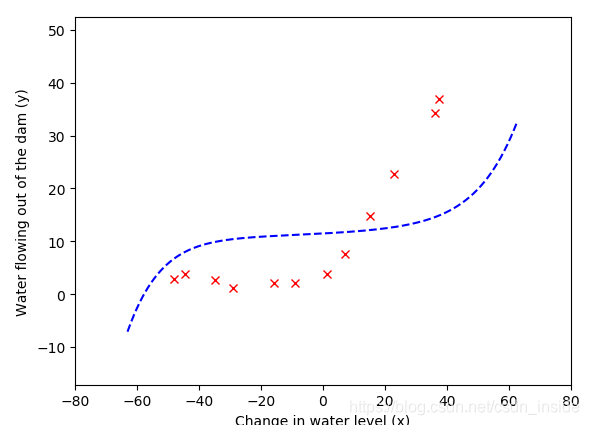
多項式迴歸:
lambda=0時,存在很嚴重的variance問題。


lambda=1時,train error跟cv error都很小,而且兩者差距不大,是個合理的lambda,中和了bias和variance。


lambda=100時,既存在嚴重的bias,又存在嚴重的variance。
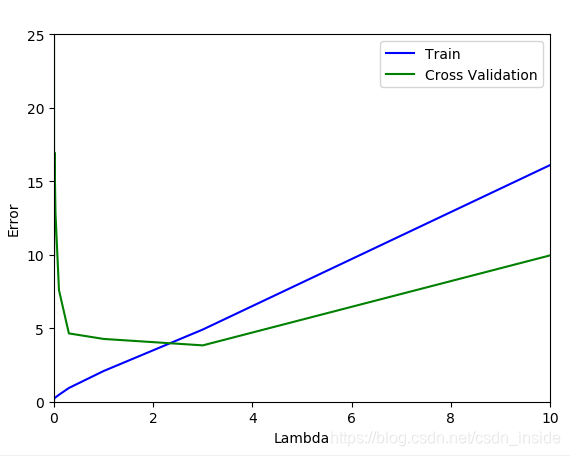
通過cv集,發現當ambda為1或者3時,train error和validation error相差最小,效果最好。
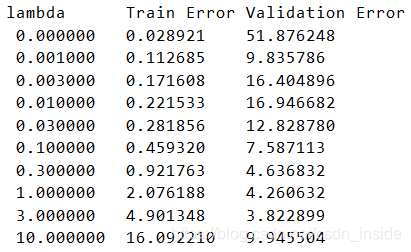
用CV集選擇了lambda之後,最後用測試集看看這個模型的效果到底如何。
![]()
