用c++實現紅黑樹的判斷、插入、遍歷操作

阿新 • • 發佈：2019-02-06

紅黑樹

紅黑樹是一棵二叉搜尋樹，它在每個節點上增加了一個儲存位來表示節點的顏色，可以是Red或Black。通過對任何一條從根到葉子簡單路徑上的顏色來約束，紅黑樹保證最長路徑不超過最短路徑的兩倍，因而近似於平衡。

紅黑樹是滿足下面紅黑性質的二叉搜尋樹：
1. 每個節點，不是紅色就是黑色的；
2. 根節點是黑色的；
3. 如果一個節點是紅色的，則它的兩個子節點是黑色的；
4. 對每個節點，從該節點到其所有後代葉節點的簡單路徑上，均包含相同數目的黑色節點；
5. 每個葉子節點都是黑色的（這裡的葉子節點是指的空節點）

思考：為什麼滿足上面的顏色約束性質，紅黑樹能保證最長路徑不超過最短路徑的兩倍？

如圖：所能增加的紅節點數最多和黑節點數目一樣多，故紅黑樹能保證最長路徑不超過最短路徑的兩倍。

一、判斷是否是紅黑樹：

//判斷是否是紅黑樹
	bool isRBTree()
	{
		int BlackNodeNum = 0;
		int curBlackNodeNum = 0;
		Node* cur = _root;

		while (cur)
		{
			if (cur->_col == BLACK)
			{
				BlackNodeNum++;
			}

			cur = cur->_left;
		}
		return _isRBTree(_root, BlackNodeNum, curBlackNodeNum);
	}

bool _isRBTree(Node* root, int BlackNodeNum, int curBlackNodeNum)
	{
		if (root == NULL)
		{
			return true;
		}

		if (root->_col == BLACK)
		{
			curBlackNodeNum++;
		}

		if (BlackNodeNum == curBlackNodeNum)
		{
			if (root->_parent == NULL)
			{
				return true;
			}
			else if (root->_col == RED && root->_col == root->_parent->_col)
			{
				return false;
			}
			else
			{
				return true;
			}
		}

		return _isRBTree(root->_left, BlackNodeNum, curBlackNodeNum) && _isRBTree(root->_right, BlackNodeNum, curBlackNodeNum);
	}

二、紅黑樹的中序遍歷：

//中序遍歷
	void InOrder()
	{
		_InOrder(_root);
	}

void _InOrder(Node* root)
	{
		if (root == NULL)
		{
			return;
		}

		_InOrder(root->_left);
		cout << root->_key << " ";
		_InOrder(root->_right);
	}

三、左單旋

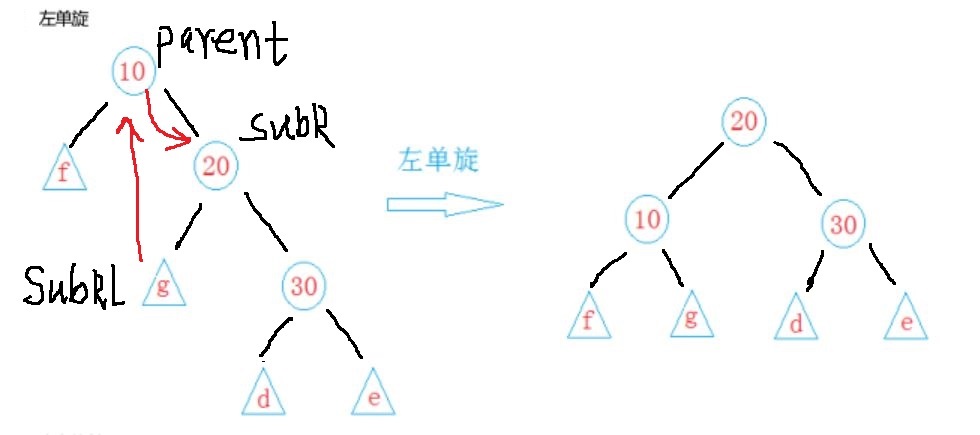
//左單旋
	void RotateL(Node*& parent)
	{
		Node* subR = parent->_right;
		Node* subRL = subR->_left;

		parent->_right = subRL;
		if (subRL)
		{
			subRL->_parent = parent;
		}

		subR->_left = parent;
		subR->_parent = parent->_parent;
		parent->_parent = subR;
		parent = subR;

		if (parent->_parent == NULL)
		{
			_root = parent;
		}
		else if (parent->_parent->_key > parent->_key)
		{
			parent->_parent->_left = parent;
		}
		else if ( parent->_parent->_key<parent->_key )
		{
			parent->_parent->_right = parent;
		}
	}

四、右單旋

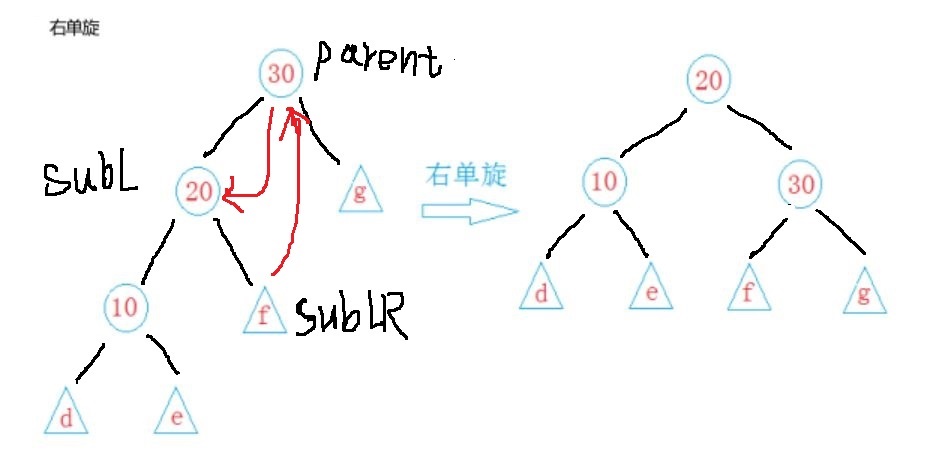
//右單旋
	void RotateR(Node*& parent)
	{
		Node* subL = parent->_left;
		Node* subLR = subL->_right;

		parent->_left = subLR;
		if (subLR)
		{
			subLR->_parent = parent;
		}

		subL->_right = parent;
		subL->_parent = parent->_parent;
		parent->_parent = subL;

		parent = subL;

		if (parent->_parent == NULL)
		{
			_root = parent;
		}
		else if (parent->_parent->_key > parent->_key)
		{
			parent->_parent->_left = parent;
		}
		else if (parent->_parent->_key < parent->_key)
		{
			parent->_parent->_right = parent;
		}

	}

五、插入的三種情況
ps:cur為當前節點，p為父節點，g為祖父節點，u為叔叔節點
1.第一種情況
cur為紅，p為紅，g為黑，u存在且為紅，則將p,u改為黑，g改為紅，然後把g當成cur，繼續向上調整。

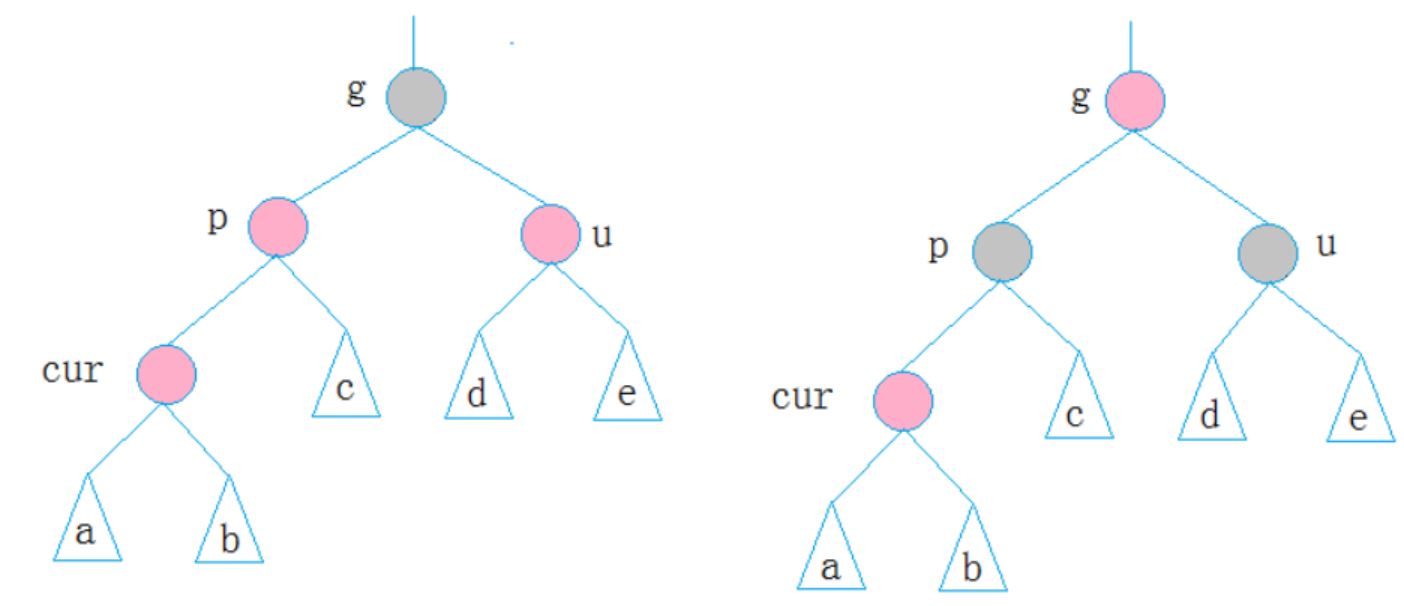
2.第二種情況
cur為紅，p為紅，g為黑，u不存在/u為黑
p為g的左孩子，cur為p的左孩子，則進行右單旋轉；相反，p為g的右孩子，cur為p的右孩子，則進行左單旋轉，p、g變色--p變黑，g變紅

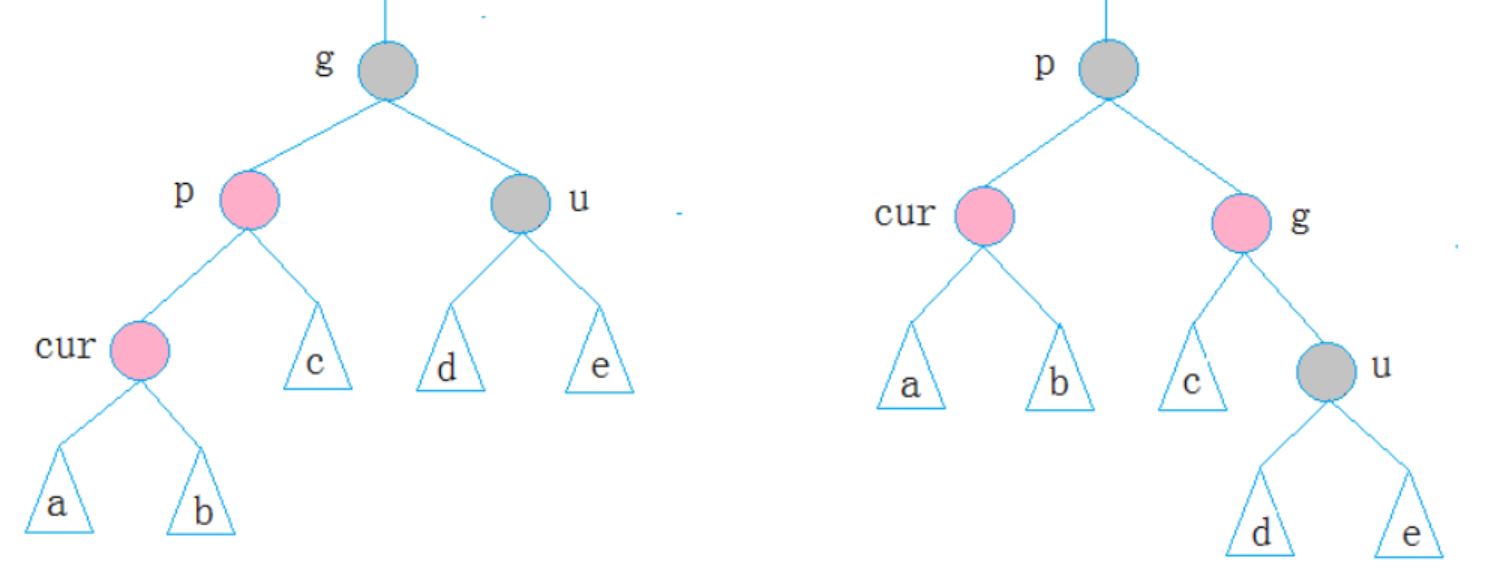
3.第三種情況
cur為紅，p為紅，g為黑，u不存在/u為黑
p為g的左孩子，cur為p的右孩子，則針對p做左單旋轉；相反，p為g的右孩子，cur為p的左孩子，則針對p做右單旋轉，則轉換成了情況2

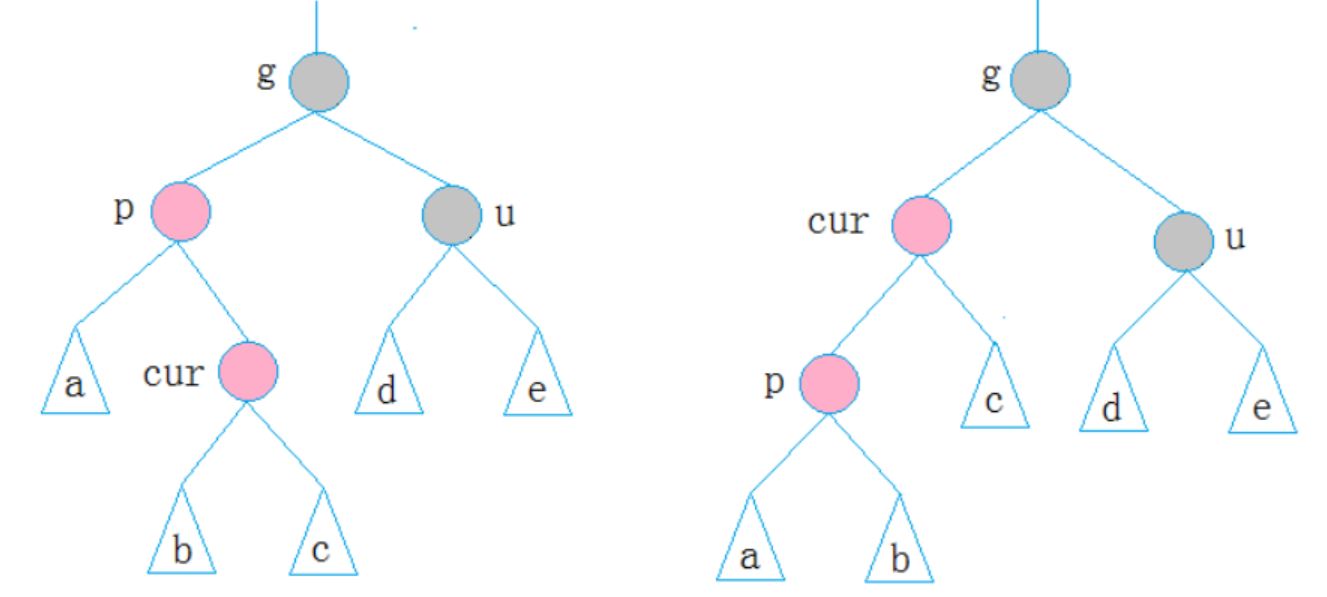
上面已經把每種情況基本列出來了，其他相反的情況類似，反過來寫一下就行了，具體詳細過程參考程式碼。

//紅黑樹的插入操作
	bool Insert(const K& key, const V& value)
	{
		if (_root == NULL)
		{
			_root = new Node(key, value);
			_root->_col = BLACK;
			return true;
		}

		Node* parent = NULL;
		Node* cur = _root;
		while (cur)
		{
			if (cur->_key > key)
			{
				parent = cur;
				cur = cur->_left;
			}
			else if (cur->_key < key)
			{
				parent = cur;
				cur = cur->_right;
			}
			else
			{
				return false;
			}
		}

		//插入位置  
		if (parent->_key >key)
		{
			cur = new Node(key, value);
			parent->_left = cur;
			cur->_parent = parent;
		}
		else if (parent->_key < key)
		{
			cur = new Node(key, value);
			parent->_right = cur;
			cur->_parent = parent;
		}

		//插入以後，進行調整  
		while (cur != _root && parent->_col == RED)
		{
			Node* grandfather = parent->_parent;
			Node* uncle = NULL;
			//左邊的情況  
			if (parent == grandfather->_left)
			{
				//情況一  
				uncle = grandfather->_right;
				if (uncle && uncle->_col == RED)
				{
					//1. 不需要旋轉  
					if (cur == parent->_left)
					{
						grandfather->_col = RED;
						parent->_col = BLACK;
						uncle->_col = BLACK;

						cur = grandfather;
						parent = cur->_parent;
					}

					//2.需要旋轉  
					else if (cur == parent->_right)
					{
						RotateL(parent);
						grandfather->_col = RED;
						parent->_col = BLACK;
						uncle->_col = BLACK;

						cur = grandfather;
						parent = cur->_parent;
					}

				}

				//情況二，三 
				else if (uncle == NULL || (uncle && uncle->_col == BLACK))
				{
					if (cur == parent->_right)
					{
						RotateL(parent);
					}
					parent->_col = BLACK;
					grandfather->_col = RED;
					RotateR(grandfather);
					break;
				}
			}
			//右邊的情況  
			else if (parent == grandfather->_right)
			{
				//情況一
				uncle = grandfather->_left;
				if (uncle && uncle->_col == RED)
				{
					//1.不需要旋轉  
					if (cur == parent->_right)
					{
						uncle->_col = BLACK;
						grandfather->_col = RED;
						parent->_col = BLACK;

						cur = grandfather;
						parent = cur->_parent;
					}

					//2.需要旋轉  
					else if (cur == parent->_left)
					{
						uncle->_col = BLACK;
						grandfather->_col = RED;
						parent->_col = BLACK;
						RotateR(parent);

						cur = grandfather;
						parent = cur->_parent;
					}
				}
				//情況二，三
				else if (uncle == NULL || (uncle && uncle->_col == BLACK))
				{
					if (cur == parent->_left)
					{
						RotateR(parent);
					}
					parent->_col = BLACK;
					grandfather->_col = RED;
					RotateL(grandfather);
					break;
				}
			}
		}
		_root->_col = BLACK;
		return true;
	}

紅黑樹和AVL樹的比較：

紅黑樹和AVL樹都是高效的平衡二叉樹，增刪查改的時間複雜度都是O(lg(N))，紅黑樹的不追求完全平衡，保證最長路徑不超過最短路徑的2倍，相對而言，降低了旋轉的要求，所以效能會優於AVL樹，所以實際運用中紅黑樹更多。

完整程式碼及測試用例：

#include<iostream>
using namespace std;

enum colour
{
	RED,
	BLACK,
};

template<class K, class V>
struct RBTreeNode
{
	int _col;
	K _key;
	V _value;
	RBTreeNode<K, V>* _left;
	RBTreeNode<K, V>* _right;
	RBTreeNode<K, V>* _parent;

	RBTreeNode(const K& key, const V& value)
		:_key(key)
		, _value(value)
		, _col(RED)
		, _left(NULL)
		, _right(NULL)
		, _parent(NULL)
	{}

};


template<class K, class V>
class RBTree
{
	typedef RBTreeNode<K, V> Node;
public:
	RBTree()
		:_root(NULL)
	{}

	//紅黑樹的插入操作
	bool Insert(const K& key, const V& value)
	{
		if (_root == NULL)
		{
			_root = new Node(key, value);
			_root->_col = BLACK;
			return true;
		}

		Node* parent = NULL;
		Node* cur = _root;
		while (cur)
		{
			if (cur->_key > key)
			{
				parent = cur;
				cur = cur->_left;
			}
			else if (cur->_key < key)
			{
				parent = cur;
				cur = cur->_right;
			}
			else
			{
				return false;
			}
		}

		//插入位置  
		if (parent->_key >key)
		{
			cur = new Node(key, value);
			parent->_left = cur;
			cur->_parent = parent;
		}
		else if (parent->_key < key)
		{
			cur = new Node(key, value);
			parent->_right = cur;
			cur->_parent = parent;
		}

		//插入以後，進行調整  
		while (cur != _root && parent->_col == RED)
		{
			Node* grandfather = parent->_parent;
			Node* uncle = NULL;
			//左邊的情況  
			if (parent == grandfather->_left)
			{
				//情況一  
				uncle = grandfather->_right;
				if (uncle && uncle->_col == RED)
				{
					//1. 不需要旋轉  
					if (cur == parent->_left)
					{
						grandfather->_col = RED;
						parent->_col = BLACK;
						uncle->_col = BLACK;

						cur = grandfather;
						parent = cur->_parent;
					}

					//2.需要旋轉  
					else if (cur == parent->_right)
					{
						RotateL(parent);
						grandfather->_col = RED;
						parent->_col = BLACK;
						uncle->_col = BLACK;

						cur = grandfather;
						parent = cur->_parent;
					}

				}

				//情況二，三 
				else if (uncle == NULL || (uncle && uncle->_col == BLACK))
				{
					if (cur == parent->_right)
					{
						RotateL(parent);
					}
					parent->_col = BLACK;
					grandfather->_col = RED;
					RotateR(grandfather);
					break;
				}
			}
			//右邊的情況  
			else if (parent == grandfather->_right)
			{
				//情況一
				uncle = grandfather->_left;
				if (uncle && uncle->_col == RED)
				{
					//1.不需要旋轉  
					if (cur == parent->_right)
					{
						uncle->_col = BLACK;
						grandfather->_col = RED;
						parent->_col = BLACK;

						cur = grandfather;
						parent = cur->_parent;
					}

					//2.需要旋轉  
					else if (cur == parent->_left)
					{
						uncle->_col = BLACK;
						grandfather->_col = RED;
						parent->_col = BLACK;
						RotateR(parent);

						cur = grandfather;
						parent = cur->_parent;
					}
				}
				//情況二，三
				else if (uncle == NULL || (uncle && uncle->_col == BLACK))
				{
					if (cur == parent->_left)
					{
						RotateR(parent);
					}
					parent->_col = BLACK;
					grandfather->_col = RED;
					RotateL(grandfather);
					break;
				}
			}
		}
		_root->_col = BLACK;
		return true;
	}

	//判斷是否是紅黑樹
	bool isRBTree()
	{
		int BlackNodeNum = 0;
		int curBlackNodeNum = 0;
		Node* cur = _root;

		while (cur)
		{
			if (cur->_col == BLACK)
			{
				BlackNodeNum++;
			}

			cur = cur->_left;
		}
		return _isRBTree(_root, BlackNodeNum, curBlackNodeNum);
	}

	//中序遍歷
	void InOrder()
	{
		_InOrder(_root);
	}

protected:
	bool _isRBTree(Node* root, int BlackNodeNum, int curBlackNodeNum)
	{
		if (root == NULL)
		{
			return true;
		}

		if (root->_col == BLACK)
		{
			curBlackNodeNum++;
		}

		if (BlackNodeNum == curBlackNodeNum)
		{
			if (root->_parent == NULL)
			{
				return true;
			}
			else if (root->_col == RED && root->_col == root->_parent->_col)
			{
				return false;
			}
			else
			{
				return true;
			}
		}

		return _isRBTree(root->_left, BlackNodeNum, curBlackNodeNum) && _isRBTree(root->_right, BlackNodeNum, curBlackNodeNum);
	}


	void _InOrder(Node* root)
	{
		if (root == NULL)
		{
			return;
		}

		_InOrder(root->_left);
		cout << root->_key << " ";
		_InOrder(root->_right);
	}

	//左單旋
	void RotateL(Node*& parent)
	{
		Node* subR = parent->_right;
		Node* subRL = subR->_left;

		parent->_right = subRL;
		if (subRL)
		{
			subRL->_parent = parent;
		}

		subR->_left = parent;
		subR->_parent = parent->_parent;
		parent->_parent = subR;
		parent = subR;

		if (parent->_parent == NULL)
		{
			_root = parent;
		}
		else if (parent->_parent->_key > parent->_key)
		{
			parent->_parent->_left = parent;
		}
		else if ( parent->_parent->_key<parent->_key )
		{
			parent->_parent->_right = parent;
		}
	}

	//右單旋
	void RotateR(Node*& parent)
	{
		Node* subL = parent->_left;
		Node* subLR = subL->_right;

		parent->_left = subLR;
		if (subLR)
		{
			subLR->_parent = parent;
		}

		subL->_right = parent;
		subL->_parent = parent->_parent;
		parent->_parent = subL;

		parent = subL;

		if (parent->_parent == NULL)
		{
			_root = parent;
		}
		else if (parent->_parent->_key > parent->_key)
		{
			parent->_parent->_left = parent;
		}
		else if (parent->_parent->_key < parent->_key)
		{
			parent->_parent->_right = parent;
		}

	}

protected:
	Node* _root;
};


void TestRBtree()
{
	RBTree<int, int>RBT;
	int arr[10]= { 1, 2,5, 12, 16, 18, 26, 3, 99,666 };

	for (int i = 0; i < 10; i++)
	{
		RBT.Insert(arr[i], i);
	}
	
	RBT.InOrder();
	cout << endl;

	cout << "isRBTree? ->:" << RBT.isRBTree() << endl;

}

int main()
{
	TestRBtree();
	system("pause");
	return 0;
}

執行結果：
1 2 3 5 12 16 18 26 99 666
isRBTree? ->:1
請按任意鍵繼續. . .

用c++實現紅黑樹的判斷、插入、遍歷操作

用c++實現紅黑樹的判斷、插入、遍歷操作

c++實現紅黑樹

用Java實現紅黑樹的完整程式碼

C++實現紅黑樹（插入功能）

Java實現二叉樹的創建和遍歷操作（有更新）

c++ STL 紅黑樹實現

紅黑樹-RBT（二、基本操作之左旋）

基於Java實現紅黑樹的基本操作

【C++STL/紅黑樹】POJ 3481 DoubleQueue

建立紅黑樹（左旋、右旋、插入、維護）程式碼+驗證

用C++實現二叉樹的三種遍歷方式

筆記：紅黑樹旋轉和插入

利用棧結構實現二叉樹的非遞迴遍歷，求二叉樹深度、葉子節點數、兩個結點的最近公共祖先及二叉樹結點的最大距離

資料結構——紅黑樹的資料插入操作

使用java實現二叉樹的非遞迴遍歷

SBS（2）-- 平衡二叉樹判斷演算法（後續遍歷）

python 實現二叉樹的深度&&廣度優先遍歷

資料結構——二叉樹的結點插入與遍歷

經典演算法：紅黑樹的C語言實現 ( 插入、刪除 )

紅黑樹C++實現

用c++實現紅黑樹的判斷、插入、遍歷操作

相關推薦