c++ STL 紅黑樹實現
紅黑樹是一種自平衡二叉查詢樹,它的操作有著良好的最壞情況執行時間,並且在實踐中是高效的: 它可以在O(log n)時間內做查詢,插入和刪除,這裡的n是樹中元素的數目。
紅黑樹應用:
1.linux核心中,程序的虛擬地址區間由紅黑樹組織管理
2.nginx中,超時時間由紅黑樹組織管理
3.C++ STL中,C++中set,multiset,map,multimap集合模板類都是在STL紅黑樹的基礎之上實現的
......
下面看紅黑樹在gcc中C++標準庫的實現,只關注結點的插入、刪除及相應的樹平衡操作
I.紅黑樹的結點
/* gcc-4.4.5/libstdc++-v3/include/bits/stl_tree.h */ /* /usr/include/c++/4.4.4/bits/stl_tree.h */ 85 enum _Rb_tree_color { _S_red = false, _S_black = true }; 86 87 struct _Rb_tree_node_base 88 { 89 typedef _Rb_tree_node_base* _Base_ptr; 90 typedef const _Rb_tree_node_base* _Const_Base_ptr; 91 92 _Rb_tree_color _M_color; 93 _Base_ptr _M_parent; 94 _Base_ptr _M_left; 95 _Base_ptr _M_right; 96 97 static _Base_ptr 98 _S_minimum(_Base_ptr __x) 99 { 100 while (__x->_M_left != 0) __x = __x->_M_left; 101 return __x; 102 } 103 104 static _Const_Base_ptr 105 _S_minimum(_Const_Base_ptr __x) 106 { 107 while (__x->_M_left != 0) __x = __x->_M_left; 108 return __x; 109 } 110 111 static _Base_ptr 112 _S_maximum(_Base_ptr __x) 113 { 114 while (__x->_M_right != 0) __x = __x->_M_right; 115 return __x; 116 } 117 118 static _Const_Base_ptr 119 _S_maximum(_Const_Base_ptr __x) 120 { 121 while (__x->_M_right != 0) __x = __x->_M_right; 122 return __x; 123 } 124 };
II.結點的插入
結點的插入主要分以下兩個步驟:
1.我們首先以二叉查詢樹的方法增加節點並標記它為紅色。(如果設為黑色,就會導致根到葉子的路徑上有一條路上,多一個額外的黑節點,這個是很難調整的。但是設為紅色節點後,可能會導致出現兩個連續紅色節點的衝突,那麼可以通過顏色調換(color flips)和樹旋轉來調整。)
2.出現連紅時做插入平衡操作
i.插入平衡操作(消除連紅)
__x:需要做插入平衡操作的結點
__p:__x的父節點
__xpp:__x的祖父節點
__y:__x的叔父節點
出現連紅(__x,__p為紅色,__xpp為黑色)時會有以下三種情況(只看__p是__xpp左兒子的情況)
1.叔父節點是紅色,則不能通過翻轉/顏色調換使樹重新平衡,只能做顏色調換並向祖父節點遞迴做平衡操作
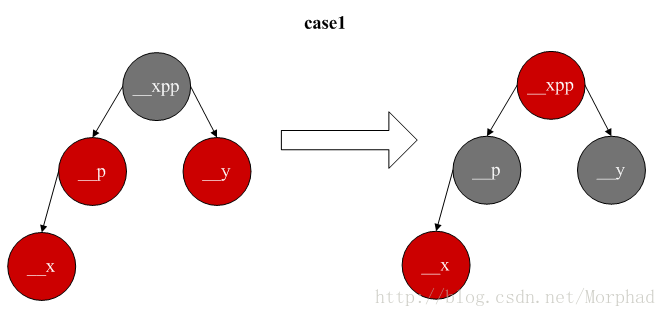
2.叔父節點是黑色,__x是__p的左兒子,通過祖父節點右翻轉和顏色調換可使樹平衡
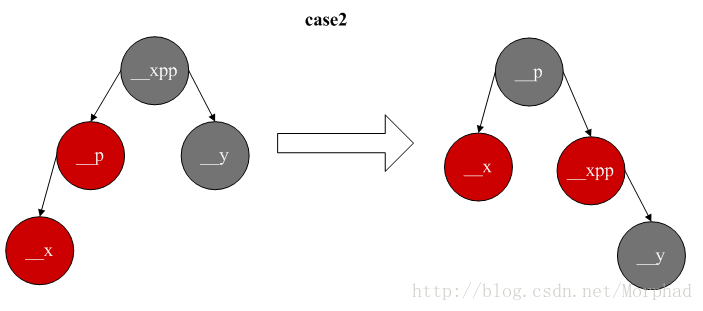
3.叔父節點是黑色,__x是__p的右兒子,可以通過__p左翻轉和顏色調換變成第二種情況,做相應的操作進而使樹平衡
ii.結點插入實現
/* gcc-4.4.5/libstdc++-v3/src/tree.cc */ 160 void 161 _Rb_tree_insert_and_rebalance(const bool __insert_left, 162 _Rb_tree_node_base* __x, 163 _Rb_tree_node_base* __p, 164 _Rb_tree_node_base& __header) 165 { 166 _Rb_tree_node_base *& __root = __header._M_parent; 167 168 // Initialize fields in new node to insert. 169 __x->_M_parent = __p; 170 __x->_M_left = 0; 171 __x->_M_right = 0; 172 __x->_M_color = _S_red; 173 174 // Insert. 175 // Make new node child of parent and maintain root, leftmost and 176 // rightmost nodes. 177 // N.B. First node is always inserted left. 178 if (__insert_left) 179 { 180 __p->_M_left = __x; // also makes leftmost = __x when __p == &__header 181 182 if (__p == &__header) 183 { 184 __header._M_parent = __x; 185 __header._M_right = __x; 186 } 187 else if (__p == __header._M_left) 188 __header._M_left = __x; // maintain leftmost pointing to min node 189 } 190 else 191 { 192 __p->_M_right = __x; 193 194 if (__p == __header._M_right) 195 __header._M_right = __x; // maintain rightmost pointing to max node 196 } /* 當結點與父結點出現連紅的情況,需要做樹平衡操作;直到樹根為止,當向上遞迴到樹根且樹根結點是紅色時,會修改樹根結點為黑色進而增加了樹的深度 */ 197 // Rebalance. 198 while (__x != __root 199 && __x->_M_parent->_M_color == _S_red) 200 { 201 _Rb_tree_node_base* const __xpp = __x->_M_parent->_M_parent; 202 203 if (__x->_M_parent == __xpp->_M_left) /* 父節點是祖父節點的左兒子,父節點是祖父的右兒子與其操作一致,只不過將一些操作由左變成右、由右變成左 */ 204 { 205 _Rb_tree_node_base* const __y = __xpp->_M_right; /* 叔父節點 */ 206 if (__y && __y->_M_color == _S_red) /* 叔父節點是紅色,則不能通過翻轉來平衡樹,只能向祖父節點遞迴平衡 */ 207 { 208 __x->_M_parent->_M_color = _S_black; 209 __y->_M_color = _S_black; 210 __xpp->_M_color = _S_red; 211 __x = __xpp; 212 } 213 else /* 叔父節點是黑色,則可以通過翻轉來平衡樹 */ 214 { 215 if (__x == __x->_M_parent->_M_right) /* 節點是父節點的右兒子,翻轉將父節點變成節點的左兒子 */ 216 { 217 __x = __x->_M_parent; 218 _Rb_tree_rotate_left(__x, __root); 219 } 220 __x->_M_parent->_M_color = _S_black; 221 __xpp->_M_color = _S_red; 222 _Rb_tree_rotate_right(__xpp, __root); /* 祖父節點右翻轉使樹平衡 */ 223 } 224 } 225 else 226 { 227 _Rb_tree_node_base* const __y = __xpp->_M_left; 228 if (__y && __y->_M_color == _S_red) 229 { 230 __x->_M_parent->_M_color = _S_black; 231 __y->_M_color = _S_black; 232 __xpp->_M_color = _S_red; 233 __x = __xpp; 234 } 235 else 236 { 237 if (__x == __x->_M_parent->_M_left) 238 { 239 __x = __x->_M_parent; 240 _Rb_tree_rotate_right(__x, __root); 241 } 242 __x->_M_parent->_M_color = _S_black; 243 __xpp->_M_color = _S_red; 244 _Rb_tree_rotate_left(__xpp, __root); 245 } 246 } 247 } 248 __root->_M_color = _S_black; 249 }
III.結點的刪除
結點的刪除主要分以下兩個步驟:
1.如果需要刪除的節點有兩個兒子,那麼問題可以被轉化成刪除另一個只有一個兒子的節點的問題;刪除相應的結點
2.刪除的結點是黑色時,破壞了樹的平衡,則需做刪除平衡操作
i.刪除平衡操作(刪除了黑色結點需要做刪除平衡操作,通過新增黑色結點來使樹重新平衡)
__x:需要做刪除平衡操作的結點
__x_parent:__x的父節點
__w:__x的兄弟節點
__wl:__w的左兒子
__wr:__w的右兒子
需要刪除平衡操作時會有以下五種情況(只看__x是__x_parent左兒子的情況)
1.__x是紅色的,則直接將其變成黑色即可
2.__x是黑色或為NULL
2.1__w是黑色
2.1.1右兒子是紅色,則可通過__w左翻轉和顏色調換使樹重新平衡
2.1.2左兒子是紅色,則可通過__w右翻轉和顏色調換,變成2.1.1的情況
2.1.3左、右兒子都不是紅色,則要做顏色調換,並且向上遞迴做平衡樹操作
2.2__w是紅色
通過__x_parent的左翻轉和顏色調換變成2.1的情況
ii.結點刪除實現
251 _Rb_tree_node_base*
252 _Rb_tree_rebalance_for_erase(_Rb_tree_node_base* const __z,
253 _Rb_tree_node_base& __header)
254 {
255 _Rb_tree_node_base *& __root = __header._M_parent;
256 _Rb_tree_node_base *& __leftmost = __header._M_left;
257 _Rb_tree_node_base *& __rightmost = __header._M_right;
258 _Rb_tree_node_base* __y = __z;
259 _Rb_tree_node_base* __x = 0;
260 _Rb_tree_node_base* __x_parent = 0;
261
262 if (__y->_M_left == 0) // __z has at most one non-null child. y == z.
263 __x = __y->_M_right; // __x might be null.
264 else
265 if (__y->_M_right == 0) // __z has exactly one non-null child. y == z.
266 __x = __y->_M_left; // __x is not null.
267 else
268 {
269 // __z has two non-null children. Set __y to
270 __y = __y->_M_right; // __z's successor. __x might be null.
271 while (__y->_M_left != 0)
272 __y = __y->_M_left;
273 __x = __y->_M_right;
274 }
/*
* 如果需要刪除的節點有兩個兒子(為了表述方便,這裡所指的兒子,為非葉子節點的兒子),那麼問題可以被轉化成刪除另一個只有一個兒子的節點的問題
* 通過互換要刪除節點的右子樹的最小元素與要刪除節點的值,再刪除右子樹的最小元素節點(必定有少於兩個非葉子的兒子),這就把問題簡化為如何刪除最多有一個兒子的節點的問題
* __y : 實際要刪除的節點
* __x : 實際要刪除的節點的兒子(非葉子節點或NULL),__y是黑色則通過__x的路徑少了一個黑色結點,所以要平衡的該結點的子樹
*/
275 if (__y != __z) /* 實際刪除的節點與要刪除的節點不相同,則將實際刪除節點與要刪除節點互換,並刪除要刪除的節點,最後由__y指向實際刪除的節點 */
276 {
/* 這裡是relink而不是交換節點的值,是因為如果是交換節點的值那麼對應物件的地址也會發生變化,通過地址訪問的話會出現問題 */
277 // relink y in place of z. y is z's successor
278 __z->_M_left->_M_parent = __y;
279 __y->_M_left = __z->_M_left;
280 if (__y != __z->_M_right)
281 {
282 __x_parent = __y->_M_parent;
283 if (__x) __x->_M_parent = __y->_M_parent;
284 __y->_M_parent->_M_left = __x; // __y must be a child of _M_left
285 __y->_M_right = __z->_M_right;
286 __z->_M_right->_M_parent = __y;
287 }
288 else
289 __x_parent = __y;
290 if (__root == __z)
291 __root = __y;
292 else if (__z->_M_parent->_M_left == __z)
293 __z->_M_parent->_M_left = __y;
294 else
295 __z->_M_parent->_M_right = __y;
296 __y->_M_parent = __z->_M_parent;
297 std::swap(__y->_M_color, __z->_M_color);
298 __y = __z;
299 // __y now points to node to be actually deleted
300 }
301 else /* 刪除結點__z,此時__leftmost或__rightmost可能會發生改變 */
302 { // __y == __z
303 __x_parent = __y->_M_parent;
304 if (__x)
305 __x->_M_parent = __y->_M_parent;
306 if (__root == __z)
307 __root = __x;
308 else
309 if (__z->_M_parent->_M_left == __z)
310 __z->_M_parent->_M_left = __x;
311 else
312 __z->_M_parent->_M_right = __x;
313 if (__leftmost == __z)
314 {
315 if (__z->_M_right == 0) // __z->_M_left must be null also
316 __leftmost = __z->_M_parent;
317 // makes __leftmost == _M_header if __z == __root
318 else
319 __leftmost = _Rb_tree_node_base::_S_minimum(__x);
320 }
321 if (__rightmost == __z)
322 {
323 if (__z->_M_left == 0) // __z->_M_right must be null also
324 __rightmost = __z->_M_parent;
325 // makes __rightmost == _M_header if __z == __root
326 else // __x == __z->_M_left
327 __rightmost = _Rb_tree_node_base::_S_maximum(__x);
328 }
329 }
330 if (__y->_M_color != _S_red) /* 如果實際刪除的結點是紅色,則不會改變樹的平衡,所以不需要處理;但是要刪除的結點是黑色,則會影響樹的平衡,所以要做樹平衡操作 */
331 {
/* 向上遞迴平衡__x子樹操作(__x子樹新增一個黑色結點),直到__x子樹平衡(__x為紅色或樹根) */
332 while (__x != __root && (__x == 0 || __x->_M_color == _S_black))
333 if (__x == __x_parent->_M_left) /* __x是左子樹;__x是右子樹時操作相同,只不過將右變成左、將左變成右 */
334 {
335 _Rb_tree_node_base* __w = __x_parent->_M_right; /* __w為平衡子樹節點的兄弟 */
/* 如果__w為紅色,通過翻轉轉換成__w是黑色的情況 */
336 if (__w->_M_color == _S_red)
337 {
338 __w->_M_color = _S_black;
339 __x_parent->_M_color = _S_red;
340 _Rb_tree_rotate_left(__x_parent, __root);
341 __w = __x_parent->_M_right;
342 }
/* 此時__w必為黑色 */
343 if ((__w->_M_left == 0 ||
344 __w->_M_left->_M_color == _S_black) &&
345 (__w->_M_right == 0 ||
346 __w->_M_right->_M_color == _S_black)) /* __w的左、右子結點沒有一個是紅色,則修改兄弟__w的顏色為紅色,向上層遞迴平衡上層子樹
347 {
348 __w->_M_color = _S_red;
349 __x = __x_parent;
350 __x_parent = __x_parent->_M_parent;
351 }
352 else
353 {
354 if (__w->_M_right == 0
355 || __w->_M_right->_M_color == _S_black) /* 如果__w的左子結點是紅色,通過右翻轉轉換成__w的右子結點是紅色的情況 */
356 {
357 __w->_M_left->_M_color = _S_black;
358 __w->_M_color = _S_red;
359 _Rb_tree_rotate_right(__w, __root);
360 __w = __x_parent->_M_right;
361 }
/* 此時__w的右子結點必為紅色 */
362 __w->_M_color = __x_parent->_M_color;
363 __x_parent->_M_color = _S_black;
364 if (__w->_M_right)
365 __w->_M_right->_M_color = _S_black;
366 _Rb_tree_rotate_left(__x_parent, __root);
367 break;
/* 通過翻轉後可使樹平衡,退出平衡操作 */
368 }
369 }
370 else
/* 同__x是左子樹操作類似 */
371 {
372 // same as above, with _M_right <-> _M_left.
373 _Rb_tree_node_base* __w = __x_parent->_M_left;
374 if (__w->_M_color == _S_red)
375 {
376 __w->_M_color = _S_black;
377 __x_parent->_M_color = _S_red;
378 _Rb_tree_rotate_right(__x_parent, __root);
379 __w = __x_parent->_M_left;
380 }
381 if ((__w->_M_right == 0 ||
382 __w->_M_right->_M_color == _S_black) &&
383 (__w->_M_left == 0 ||
384 __w->_M_left->_M_color == _S_black))
385 {
386 __w->_M_color = _S_red;
387 __x = __x_parent;
388 __x_parent = __x_parent->_M_parent;
389 }
390 else
391 {
392 if (__w->_M_left == 0 || __w->_M_left->_M_color == _S_black)
393 {
394 __w->_M_right->_M_color = _S_black;
395 __w->_M_color = _S_red;
396 _Rb_tree_rotate_left(__w, __root);
397 __w = __x_parent->_M_left;
398 }
399 __w->_M_color = __x_parent->_M_color;
400 __x_parent->_M_color = _S_black;
401 if (__w->_M_left)
402 __w->_M_left->_M_color = _S_black;
403 _Rb_tree_rotate_right(__x_parent, __root);
404 break;
405 }
406 }
407 if (__x) __x->_M_color = _S_black;
408 }
409 return __y;
410 }