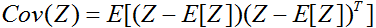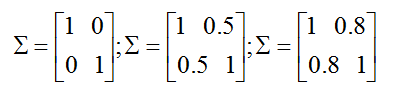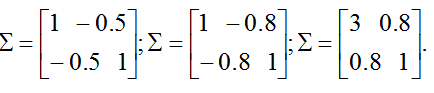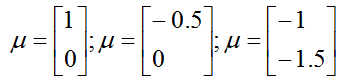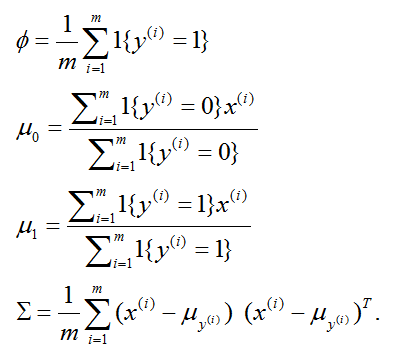第四部分  生成學習演算法

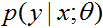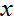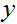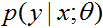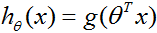到目前為止，我們主要討論了建模——給定下的的條件分佈——的學習演算法。例如，邏輯迴歸把建模成，這裡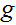是sigmoid函式。在這些講義中，我們將討論一種不同形式的學習演算法。
考慮一個分類問題，在這個分類問題中，我們想基於一個動物的一些特徵，來學習區分是大象（）還是小狗（）。給定一個訓練集，一個諸如邏輯迴歸或感知器的演算法（基本上）試圖找到一條直線—也就是一個分界線—來分離大象和狗。然後，為了把一個新動物歸類成大象或者小狗，要檢查它落在了邊界線的哪一側，相應地做出預測。
這裡有一個不同的方法。首先，看大象，我們可以建立一個大象看起來像什麼的模型。然後，看小狗，我們可以建立一個不同的小狗看起來像什麼的模型。最後，為了把一個新動物分類，我們可以把它和大象模型相比配，而且把它和小狗模型相比配，來看那個新動物是看起來更像我們訓練集中的大象，還是更像我們訓練集中的小狗。
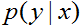
試圖直接學習的演算法（例如邏輯迴歸）或試圖學習從輸入空間直接對映到標籤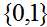的演算法（如感知器演算法），被稱作判別學習演算法(discriminative learing algorithms)。這裡，我們反而將討論試圖建模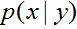（和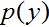）的演算法。這些演算法被稱作生成學習演算法(generative learing algorithms)。比如，如果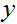表示一個樣例是一隻小狗(0)或者一隻大象（1），然後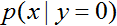是小狗特徵分佈的模型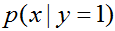，是大象特徵分佈的模型。
建完模型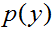（稱作類的先驗(class priors)）和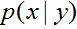，我們的演算法然後可以使用貝葉斯公式來推導給定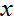時的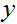的後驗分佈：

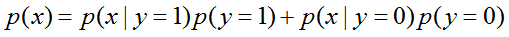
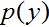這裡，分母由給出（你應該能夠核實這是標準的概率性質），因此也可以根據我們學習的

和項表示出來。實際上，如果我們在為了做出預測而計算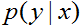，然後我們實際上不需要計算分母，因為

1  高斯判別分析
我們將要看的第一個生成學習演算法是高斯判別分析（GDA）。在這個模型中，我們將假定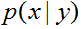服從多元正態分佈。在繼續討論GDA模型本身之前，讓我們簡單的談一下多元正態分佈的特徵。
1.1 多元正態分佈
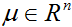
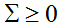
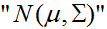
n維的多元正態分佈，也稱作多元高斯分佈，是由一個均值向量(mean vector)和一個協方差矩陣(covariance matrix)引數化的，這裡，是對稱的和半正定的。也寫作，它的密度由


給出。在上面的等式中，表示矩陣的行列式。
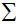
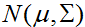
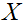
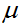
對於一個服從的隨機變數，（毫無令人意外）均值由給出：


一個向量值隨機變數Z的協方差被定義為

。這推廣了一個實數值隨機變數的方差的符號。協方差也可以被定義成。（你應該能夠向自己證明這兩個定義是相等的。）如果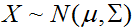，那麼


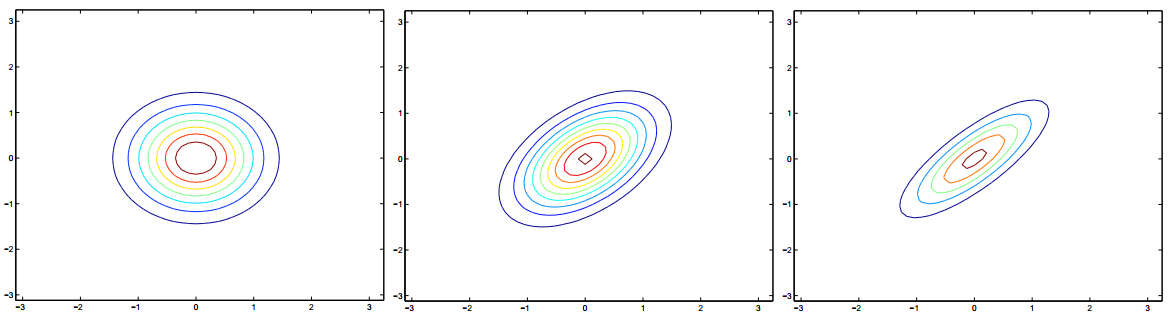
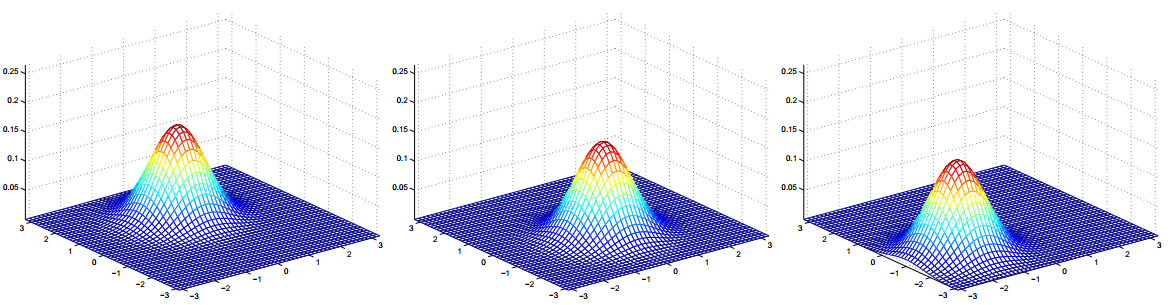
這裡有一些高斯分佈的密度看起來像什麼的例子：




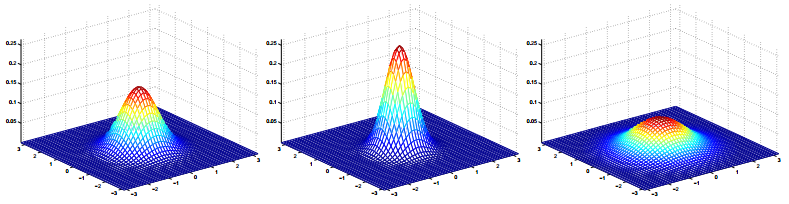
最左邊的圖形顯示了一個零均值（即，2 x 1的0-向量）和協方差矩陣（2 x 2的單位矩陣）的高斯分佈（的密度）。一個具有零均值和單位協方差（陣）的高斯分佈也被稱為標準正態分佈(standard normal distribution)。中間的圖形顯示了一個具有零均值和的高斯分佈的密度；最右邊的圖形顯示了一個零均值和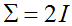的高斯分佈的密度。我們看到，隨著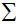變得更大，高斯分佈變得更“分散”，當它變得更小，分佈變得更“壓緊”的。
讓我們再看一些例子。


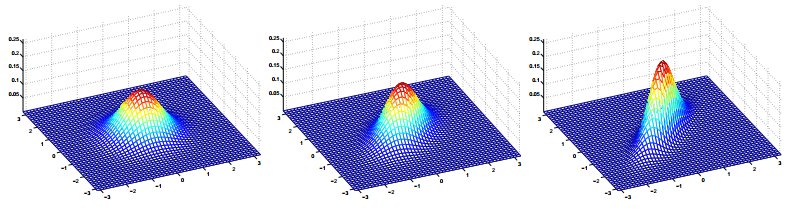
上面的圖形顯示了0均值和協方差矩陣分別為

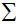
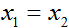
的高斯分佈。最左邊的圖形顯示了熟悉的標準正態分佈，我們看到當我們增加中的非對角元素，沿45°直線（由給出的）密度變得更“壓緊”。當我們看相同三個密度的輪廓時，我們可以更清晰地看到這些：

這裡是最後一組通過變化產生的例子。


上邊的圖形分別使用了


從最左邊和中間的圖形，我們看到通過減小協方差矩陣的對角線元素，密度現在再次變得“壓緊的”，但是是相反的方向。最後，當我們改變引數，輪廓一般會形成橢圓形的（最右邊的圖形顯示了這樣一個例子）。
作為我們最後一組例子，固定，通過改變，我們也可以在周圍移動密度的均值。


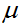
上面的圖形由，均值向量分別為


所生成的。

1.2 高斯判別分析模型
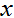
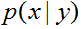
當我們有一個輸入特徵是連續值隨機變數的分類問題時，我們然後可以使用高斯判別分析（GDA）模型,這個模型使用多元正態分佈建模。模型為：


寫出這個分佈，它是：


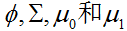
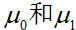
這裡，我們模型的引數是。（注意，儘管模型中有兩個不同的均值,但這個模型通常被使用時只使用一個協方差矩陣。）資料的log-似然由


給出。
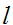
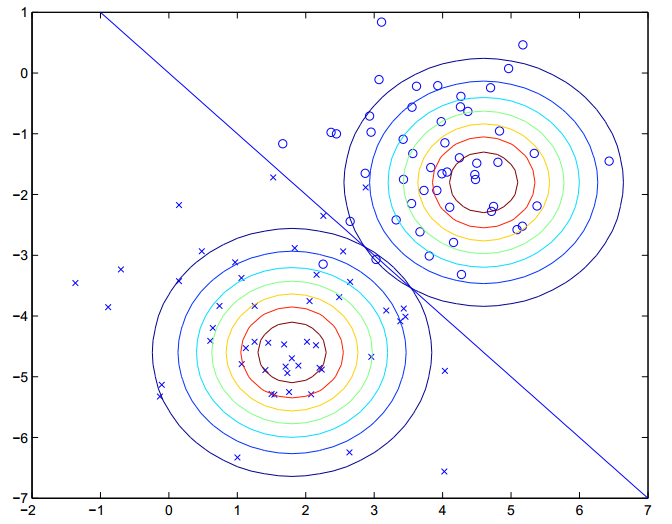
通過關於引數來最大化，我們發現引數的最大似然估計為：


形象地，演算法在做什麼如下所示：


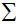
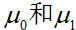
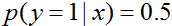
圖形中顯示的是訓練集，和兩個已經擬合了兩類資料的高斯分佈的輪廓。注意，兩個高斯分佈有相同形狀和朝向的輪廓，因為他們共有一個協方差矩陣，但是他們有不同的均值。圖形中也顯示了一條給出決策邊界的直線，在直線上。在邊界的一側，我們預測是最有可能的結果，在另一側，我們預測（是最有可能的結果）。

1.3 討論：GDA和邏輯迴歸

GDA模型同邏輯迴歸有一個有趣的關係。如果我們把看作的函式，我們將會發現它可以被表示成


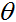
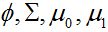
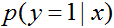
這樣的形式，在這裡是某個合適的的函式。這恰好是邏輯迴歸——一個判別演算法——用來建模的形式。
我們什麼時候更喜歡哪個模型呢？一般而言，當訓練相同的資料集時，GDA和邏輯迴歸將給出不同的決策邊界。哪個更好？
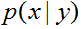
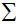
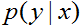
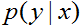
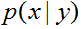
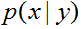
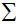
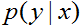
我們剛剛表明如果服從（共有的）多元高斯分佈，然後必然是一個邏輯函式。然而，逆命題是不對的；也就是說，是一個邏輯函式不一定意味著是多元高斯分佈。這表明，相比邏輯迴歸，GDA關於資料做了更強的建模假設。事實證明，當這些建模假設是正確的，GDA將會更好的擬合數據，是一個更好的模型。明確地說，當確實是（共有的）高斯分佈，然後GDA是漸進有效(asymptotically efficient)的。非正式地，這意味著在非常大的訓練集中（大的m），沒有演算法嚴格地比GDA更好（就評估的精確性而言）。特別是，可以證明，在這個背景下，GDA是一個比邏輯迴歸更好的演算法；更一般地，即使對於小規模的訓練集，我們一般認為GDA會更好一些。
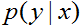
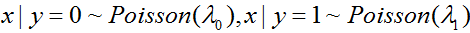
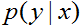
相比之下，通過做出明顯較弱的假設，邏輯迴歸對不正確的建模假設也更是魯棒和不敏感。有很多不同的假設集可以致使為一個邏輯函式的形式。比如說，如果，然後將是邏輯函式。邏輯迴歸對於像這樣的Poisson資料也工作的不錯。但是如果我們使用GDA在這樣的資料上——在這樣非高斯分佈的資料上擬合高斯分佈——那麼結果將是難以預測的，GDA可能（或可能不）工作的好。
總結：GDA做了更強的建模假設，於是當建模假設是正確的或近似正確時，它是更加資料有效的（也就是需要更少的資料就可以學習“好”）。邏輯迴歸做了弱一些的假設，因此對於建模假設中的偏差是明顯更加魯棒的。具體地說，當資料確實不是高斯分佈時，然後在大的資料集下，邏輯迴歸幾乎總是比邏輯迴歸做的好。由於這個原因，在實踐中邏輯迴歸比GDA使用的更多。（儘管關於判別vs生成模型的一些相關的考慮也適用於我們接下來要討論的樸素貝葉斯演算法，但是樸素貝葉斯演算法仍被認為是一個好的，當然也是一個很受歡迎的，分類演算法。）

本篇文章介紹了生成學習演算法的第一個演算法：判別分析演算法，並且討論了它和邏輯迴歸的關係。在下一小節中，我們將講述第二個生成學習演算法：樸素貝葉斯演算法。

想寫一寫機器學習的翻譯來鞏固一下自己的知識，同時給需要的朋友們提供參考，鑑於作者水平有限，翻譯不對或不恰當的地方，歡迎指正和建議。