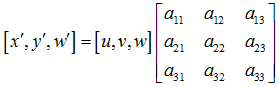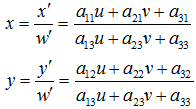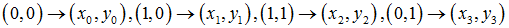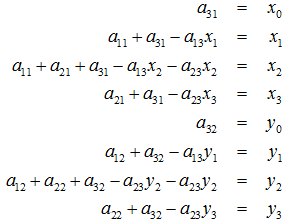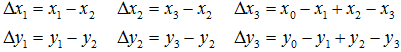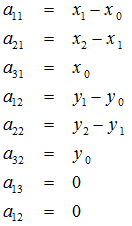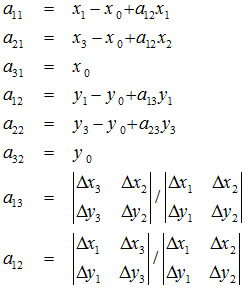透視變換(Perspective Transformation)是將圖片投影到一個新的視平面(Viewing Plane)，也稱作投影對映(Projective Mapping)。通用的變換公式為：

u,v是原始圖片左邊，對應得到變換後的圖片座標x,y,其中。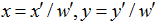
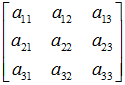
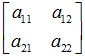
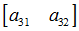
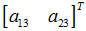
變換矩陣可以拆成4部分，表示線性變換，比如scaling，shearing和ratotion。用於平移，產生透視變換。所以可以理解成仿射等是透視變換的特殊形式。經過透視變換之後的圖片通常不是平行四邊形（除非對映視平面和原來平面平行的情況）。

重寫之前的變換公式可以得到：

所以，已知變換對應的幾個點就可以求取變換公式。反之，特定的變換公式也能新的變換後的圖片。簡單的看一個正方形到四邊形的變換：
變換的4組對應點可以表示成：

根據變換公式得到：

定義幾個輔助變數：

都為0時變換平面與原來是平行的，可以得到：

不為0時，得到：

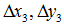
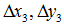
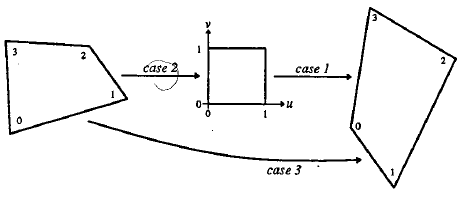
求解出的變換矩陣就可以將一個正方形變換到四邊形。反之，四邊形變換到正方形也是一樣的。於是，我們通過兩次變換：四邊形變換到正方形+正方形變換到四邊形就可以將任意一個四邊形變換到另一個四邊形。

看一段程式碼：

PerspectiveTransform::PerspectiveTransform(float inA11, float inA21, 
                                           float inA31, float inA12, 
                                           float inA22, float inA32, 
                                           float inA13, float inA23, 
                                           float inA33) : 
  a11(inA11), a12(inA12), a13(inA13), a21(inA21), a22(inA22), a23(inA23),
  a31(inA31), a32(inA32), a33(inA33) {}

PerspectiveTransform PerspectiveTransform::quadrilateralToQuadrilateral(float x0, float y0, float x1, float y1,
    float x2, float y2, float x3, float y3, float x0p, float y0p, float x1p, float y1p, float x2p, float y2p,
    float x3p, float y3p) {
  PerspectiveTransform qToS = PerspectiveTransform::quadrilateralToSquare(x0, y0, x1, y1, x2, y2, x3, y3);
  PerspectiveTransform sToQ =
    PerspectiveTransform::squareToQuadrilateral(x0p, y0p, x1p, y1p, x2p, y2p, x3p, y3p);
  return sToQ.times(qToS);
}

PerspectiveTransform PerspectiveTransform::squareToQuadrilateral(float x0, float y0, float x1, float y1, float x2,
    float y2, float x3, float y3) {
  float dx3 = x0 - x1 + x2 - x3;
  float dy3 = y0 - y1 + y2 - y3;
  if (dx3 == 0.0f && dy3 == 0.0f) {
    PerspectiveTransform result(PerspectiveTransform(x1 - x0, x2 - x1, x0, y1 - y0, y2 - y1, y0, 0.0f,
                                     0.0f, 1.0f));
    return result;
  } else {
    float dx1 = x1 - x2;
    float dx2 = x3 - x2;
    float dy1 = y1 - y2;
    float dy2 = y3 - y2;
    float denominator = dx1 * dy2 - dx2 * dy1;
    float a13 = (dx3 * dy2 - dx2 * dy3) / denominator;
    float a23 = (dx1 * dy3 - dx3 * dy1) / denominator;
    PerspectiveTransform result(PerspectiveTransform(x1 - x0 + a13 * x1, x3 - x0 + a23 * x3, x0, y1 - y0
                                     + a13 * y1, y3 - y0 + a23 * y3, y0, a13, a23, 1.0f));
    return result;
  }
}

PerspectiveTransform PerspectiveTransform::quadrilateralToSquare(float x0, float y0, float x1, float y1, float x2,
    float y2, float x3, float y3) {
  // Here, the adjoint serves as the inverse:
  return squareToQuadrilateral(x0, y0, x1, y1, x2, y2, x3, y3).buildAdjoint();
}

PerspectiveTransform PerspectiveTransform::buildAdjoint() {
  // Adjoint is the transpose of the cofactor matrix:
  PerspectiveTransform result(PerspectiveTransform(a22 * a33 - a23 * a32, a23 * a31 - a21 * a33, a21 * a32
                                   - a22 * a31, a13 * a32 - a12 * a33, a11 * a33 - a13 * a31, a12 * a31 - a11 * a32, a12 * a23 - a13 * a22,
                                   a13 * a21 - a11 * a23, a11 * a22 - a12 * a21));
  return result;
}

PerspectiveTransform PerspectiveTransform::times(PerspectiveTransform other) {
  PerspectiveTransform result(PerspectiveTransform(a11 * other.a11 + a21 * other.a12 + a31 * other.a13,
                                   a11 * other.a21 + a21 * other.a22 + a31 * other.a23, a11 * other.a31 + a21 * other.a32 + a31
                                   * other.a33, a12 * other.a11 + a22 * other.a12 + a32 * other.a13, a12 * other.a21 + a22
                                   * other.a22 + a32 * other.a23, a12 * other.a31 + a22 * other.a32 + a32 * other.a33, a13
                                   * other.a11 + a23 * other.a12 + a33 * other.a13, a13 * other.a21 + a23 * other.a22 + a33
                                   * other.a23, a13 * other.a31 + a23 * other.a32 + a33 * other.a33));
  return result;
}

void PerspectiveTransform::transformPoints(vector<float> &points) {
  int max = points.size();
  for (int i = 0; i < max; i += 2) {
    float x = points[i];
    float y = points[i + 1];
    float denominator = a13 * x + a23 * y + a33;
    points[i] = (a11 * x + a21 * y + a31) / denominator;
    points[i + 1] = (a12 * x + a22 * y + a32) / denominator;
  }
}
 

int main(){
	Mat img=imread("boy.png");
	int img_height = img.rows;
	int img_width = img.cols;
	Mat img_trans = Mat::zeros(img_height,img_width,CV_8UC3);
	PerspectiveTransform tansform = PerspectiveTransform::quadrilateralToQuadrilateral(
		0,0,
		img_width-1,0,
		0,img_height-1,
		img_width-1,img_height-1,
		150,250, // top left
		771,0, // top right
		0,1023,// bottom left
		650,1023
		);
	vector<float> ponits;
	for(int i=0;i<img_height;i++){
		for(int j=0;j<img_width;j++){
			ponits.push_back(j);
			ponits.push_back(i);
		}
	}
	tansform.transformPoints(ponits);
	for(int i=0;i<img_height;i++){
		uchar*  t= img_trans.ptr<uchar>(i);
		for (int j=0;j<img_width;j++){
			int tmp = i*img_width+j;
			int x = ponits[tmp*2];
			int y = ponits[tmp*2+1];
			if(x<0||x>(img_width-1)||y<0||y>(img_height-1))
				continue;
			uchar* p = img.ptr<uchar>(y);
			t[j*3] = p[x*3];
			t[j*3+1] = p[x*3+1];
			t[j*3+2] = p[x*3+2];
		}
	}
	imwrite("trans.png",img_trans);
	return 0;
}