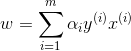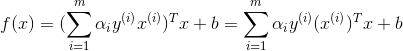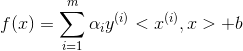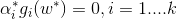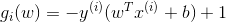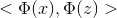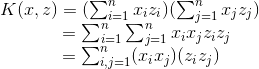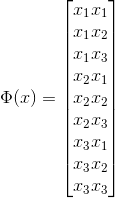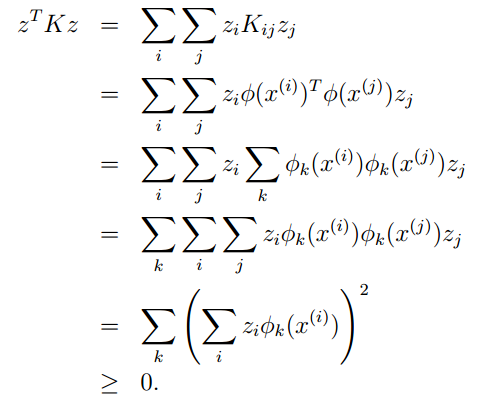支援向量機(SVM)(三)----核函式及正則化
上一節最後我們說到我們根據求得的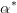
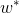
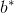
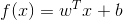
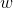
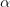
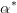
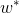
假如我們已經求得最優的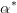
其中:
由此可以知道,若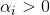
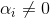
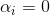
Kernels
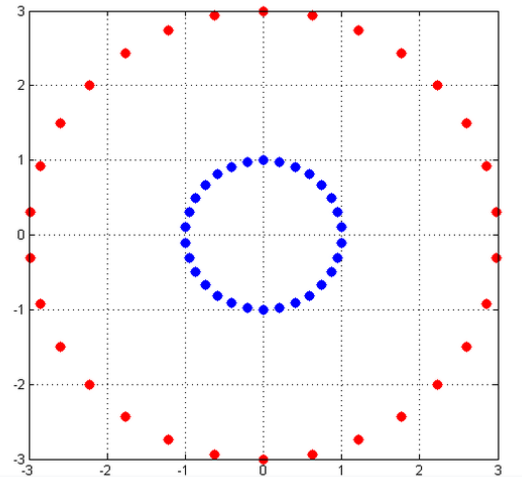
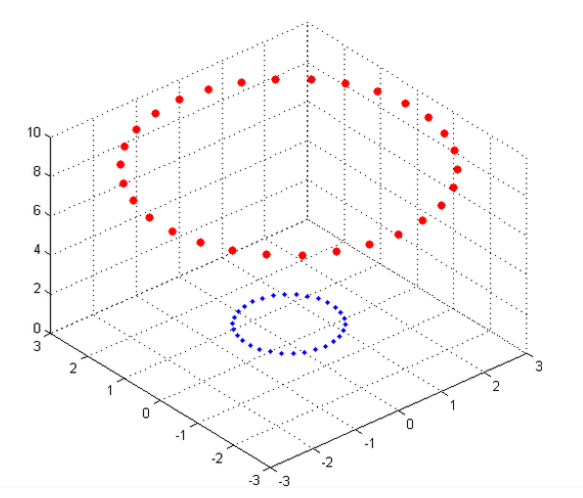
我們上次最後說明了,如果遇到線性不可分的情況,根據現有的分類函式,可能解決不了,比如,下圖(來源:知乎)
上圖中的紅點服從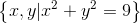


對映到三維空間之後,紅藍點變得線性可分了。核函式作用其實就是通過一個對映,把低維線性不可分的樣本點,對映到高維中,使之變得線性可分。
吳恩達老師說,“原始”的輸入我們稱之為問題的屬性,當“原始”輸入經過對映得到一個新的集合,而這個集合傳遞給學習演算法,這樣的一個新的集合稱之為特徵。SVM的輸入就是特徵而不是原始的輸入屬性。當低維線性不可分 的時候,我們把輸入屬性,對映到一個高維特徵空間,並把對映後的特徵作為新的輸入,而新的決策函式,只是把原來的內積運算<x,z>簡單替換為
核函式定義為:
其中的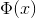
憑直覺來看,要求出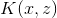
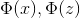
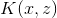
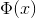
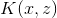
我們先看一個例子:
我們可以把上式寫成如下的形式:
假如當N=3時,那麼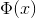
對於這個例子,我們在高維中計算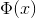
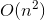
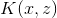
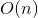
對於kernel,我們有多項式kernel,Gaussian kernel等等,那麼給定一個函式K,我們怎麼知道他是不是有效的呢?也就是說對於所有的x,z是否存在一個對映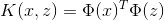
假如K是有效的,那麼有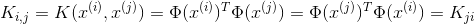
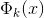
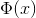
這就說明了如果K是有效的,那麼其對應的核矩陣就是半正定的。這是一個充分必要條件,也是Mercer定理。好了到此我們也說明了什麼是核函式。下一節我們將繼續上一節的話題,怎麼樣求解對偶問題的解。請看: