回溯法

1、有許多問題，當需要找出它的解集或者要求回答什麼解是滿足某些約束條件的最佳解時，往往要使用回溯法。
2、回溯法的基本做法是搜尋，或是一種組織得井井有條的，能避免不必要搜尋的窮舉式搜尋法。這種方法適用於解一些組合數相當大的問題。
3、回溯法在問題的解空間樹中，按深度優先策略，從根結點出發搜尋解空間樹。演算法搜尋至解空間樹的任意一點時，先判斷該結點是否包含問題的解。如果肯定不包含（剪枝過程），則跳過對該結點為根的子樹的搜尋，逐層向其祖先結點回溯；否則，進入該子樹，繼續按深度優先策略搜尋。

問題的解空間

問題的解向量：回溯法希望一個問題的解能夠表示成一個n元式(x1,x2,…,xn)的形式。

顯約束：對分量xi的取值限定。
隱約束：為滿足問題的解而對不同分量之間施加的約束。
解空間：對於問題的一個例項，解向量滿足顯式約束條件的所有多元組，構成了該例項的一個解空間。

注意：同一個問題可以有多種表示，有些表示方法更簡單，所需表示的狀態空間更小（儲存量少，搜尋方法簡單）。

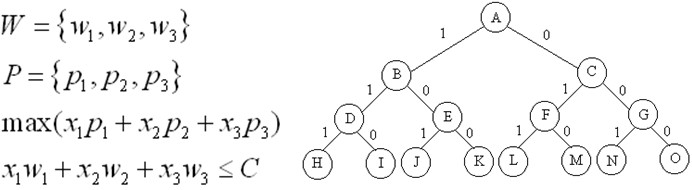
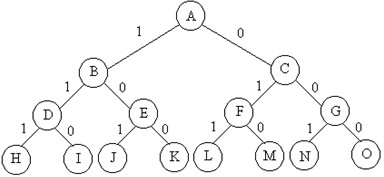
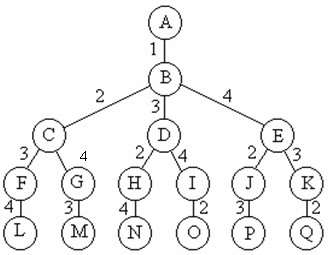
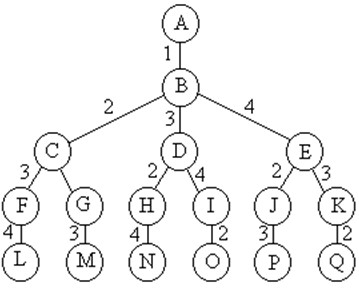
下面是n=3時的0-1揹包問題用完全二叉樹表示的解空間：

生成問題狀態的基本方法

擴充套件結點:一個正在產生兒子的結點稱為擴充套件結點
活結點:一個自身已生成但其兒子還沒有全部生成的節點稱做活結點
死結點:一個所有兒子已經產生的結點稱做死結點

深度優先的問題狀態生成法：如果對一個擴充套件結點R，一旦產生了它的一個兒子C，就把C當做新的擴充套件結點。在完成對子樹C（以C為根的子樹）的窮盡搜尋之後，將R重新變成擴充套件結點，繼續生成R的下一個兒子（如果存在）

寬度優先的問題狀態生成法：在一個擴充套件結點變成死結點之前，它一直是擴充套件結點

回溯法：為了避免生成那些不可能產生最佳解的問題狀態，要不斷地利用限界函式(bounding function)來處死(剪枝)那些實際上不可能產生所需解的活結點，以減少問題的計算量。具有限界函式的深度優先生成法稱為回溯法。（回溯法 = 窮舉 +　剪枝）

回溯法的基本思想

(1)針對所給問題，定義問題的解空間；
(2)確定易於搜尋的解空間結構；
(3)以深度優先方式搜尋解空間，並在搜尋過程中用剪枝函式避免無效搜尋。

兩個常用的剪枝函式：

• (1)約束函式：在擴充套件結點處減去不滿足約束的子數
• (2)限界函式：減去得不到最優解的子樹

用回溯法解題的一個顯著特徵是在搜尋過程中動態產生問題的解空間。在任何時刻，演算法只儲存從根結點到當前擴充套件結點的路徑。如果解空間樹中從根結點到葉結點的最長路徑的長度為h(n)，則回溯法所需的計算空間通常為O(h(n))。而顯式地儲存整個解空間則需要O(2h(n))或O(h(n)!)記憶體空間。

回溯演算法的設計步驟

回溯演算法的遞迴實現和迭代實現

遞歸回溯

回溯法對解空間作深度優先搜尋，因此，在一般情況下用遞迴方法實現回溯法。

// 針對N叉樹的遞歸回溯方法
void backtrack (int t)
{
    if (t > n) {
       // 到達葉子結點，將結果輸出
       output (x);
    }
    else {
       // 遍歷結點t的所有子結點
       for (int i = f(n,t); i <= g(n,t); i ++ ) {
           x[t] = h[i];
           // 如果不滿足剪枝條件，則繼續遍歷
           if (constraint (t) && bound (t)) 
              backtrack (t + 1);
       }
    }
}

迭代回溯

採用樹的非遞迴深度優先遍歷演算法，可將回溯法表示為一個非遞迴迭代過程。

// 針對N叉樹的迭代回溯方法
void iterativeBacktrack ()
{
    int t = 1;
    while (t > 0) {
       if (f(n,t) <= g(n,t)) {
           //  遍歷結點t的所有子結點
           for (int i = f(n,t); i <= g(n,t); i ++) {
              x[t] = h(i);
              // 剪枝
              if (constraint(t) && bound(t)) {
                  // 找到問題的解，輸出結果
                  if (solution(t)) {

                     output(x);
                  }
                  else // 未找到，向更深層次遍歷
                     t ++;
              }
           }
       }
       else {
           t--;

       }
    }

}

回溯法一般依賴的兩種資料結構：子集樹和排列樹

子集樹（遍歷子集樹需O(2n)計算時間）

void backtrack (int t)
{
    if (t > n)
       // 到達葉子結點
       output (x);
    else
       for (int i = 0;i <= 1;i ++) {
           x[t] = i;
           // 約束函式
           if ( legal(t) )
              backtrack( t+1 );
       }

}

排列樹（遍歷排列樹需要O(n!)計算時間）

void backtrack (int t)
{
    if (t > n)
       output(x);
    else

       for (int i = t;i <= n;i++) {
           // 完成全排列
           swap(x[t], x[i]);

           if (legal(t))
              backtrack(t+1);
           swap(x[t], x[i]);

       }
}

幾個典型的例子

裝載問題

問題表述：有一批共n個集裝箱要裝上2艘載重量分別為c1和c2的輪船，其中集裝箱i的重量為wi，且∑ni=1wi≤c1+c2
裝載問題要求確定是否有一個合理的裝載方案可將這個集裝箱裝上這2艘輪船。如果有，找出一種裝載方案。
解決方案：

容易證明，如果一個給定裝載問題有解，則採用下面的策略可得到最優裝載方案。
(1)首先將第一艘輪船儘可能裝滿；
(2)將剩餘的集裝箱裝上第二艘輪船。

將第一艘輪船儘可能裝滿等價於選取全體集裝箱的一個子集，使該子集中集裝箱重量之和最接近。由此可知，裝載問題等價於以下特殊的0-1揹包問題。

max∑ni=1wixi,s.t.∑ni=1wixi≤c1,xi∈0,1,1≤i≤n

解空間：
子集樹可行性約束函式(選擇當前元素)：

∑ni=1wixi≤c1
上界函式(不選擇當前元素)：
當前載重量cw+剩餘集裝箱的重量r≤當前最優載重量bestw

void backtrack (int i)
{
    // 搜尋第i層結點
    if (i > n)  // 到達葉結點
       更新最優解bestx,bestw;return;
    r -= w[i];
    if (cw + w[i] <= c) {
       // 搜尋左子樹
       x[i] = 1;
       cw += w[i];
       backtrack (i + 1);
       cw -= w[i];     
    }
    if (cw + r > bestw)  {
       x[i] = 0;  // 搜尋右子樹
       backtrack(i + 1);     
    }
    r += w[i];
}

變數解釋：
r: 剩餘重量
w: 各個集裝箱重
cw:當前總重量
x: 每個集裝箱是否被選取標誌
bestx: 最佳選取方案
bestw: 最優載重量
實現：

#include <iostream>
#include <vector>
#include <iterator>
using namespace std;

/* 裝載問題子函式
* layers: 搜尋到第layers層結點
* layers_size: layers_size總層數
* current_w: 當前承載量
* best_w: 最優載重量
* flag_x: 選取方案
* best_x: 最佳選取方案
* remainder_w:剩餘重量
* container_w:每個集裝箱的重量
* total_w: 總承載量
*/
void __backtrack (int layers,const int layers_size,
                  int current_w,int& best_w,
                  vector<int>& flag_x,vector<int>& 

best_x,
                  int remainder_w,
                  const vector<int>& container_w,
                  int total_w)
{
    if (layers > layers_size - 1) {
        // 到達葉子結點，更新最優載重量
        if (current_w < best_w || best_w == -1) {
            copy(flag_x.begin(),flag_x.end

(),best_x.begin());
            // copy(best_x.begin(),best_x.end

(),flag_x.begin());
            best_w = current_w;
        }
        return;
    }
    remainder_w -= container_w[layers];
    if (current_w + container_w[layers] <= total_w) {
        // 搜尋左子樹
        flag_x[layers] = 1;
        current_w += container_w[layers];
        __backtrack(layers + 1,layers_size,current_w,

best_w,flag_x,best_x,remainder_w,container_w,
                    total_w);
        current_w -= container_w[layers];
    }
    if (current_w + remainder_w > best_w || best_w == -

1) {
        flag_x[layers] = 0;
        __backtrack(layers + 1,layers_size,current_w,

best_w,flag_x,best_x,remainder_w,container_w,
                    total_w);
    }
    remainder_w += container_w[layers];
}
/* 裝載問題
* container_w: 各個集裝箱重量
* total_w: 總承載量
*/
void loading_backtrack (int total_w, vector<int>& 

container_w)
{
    int layers_size = container_w.size();   // 層數
    int current_w = 0;          // 當前裝載重量
    int remainder_w = total_w;  // 剩餘重量
    int best_w = -1;             // 最優載重量
    vector<int> flag_x(layers_size);    // 是否被選取標

志
    vector<int> best_x(layers_size);    // 最佳選取方案
    __backtrack(0,layers_size,current_w,

best_w,flag_x,best_x,remainder_w,container_w,
                    total_w);
    cout << "path : " ;
    copy(best_x.begin(),best_x.end

(),ostream_iterator<int>(cout," "));
    cout << endl;
    cout << "best_w = " << best_w
        << "( ";
    // 將結果輸出
    for (size_t i = 0;i < best_x.size(); ++ i) {
        if (best_x[i] == 1) {
            cout << container_w[i] << " ";
        }
    }
    cout << ")" << endl;
}

int main()
{
    const int total_w = 30;
    vector<int> container_w;
    container_w.push_back(40);
    container_w.push_back(1);
    container_w.push_back(40);
    container_w.push_back(9);
    container_w.push_back(1);
    container_w.push_back(8);
    container_w.push_back(5);
    container_w.push_back(50);
    container_w.push_back(6);

    loading_backtrack(total_w,container_w);
    return 0;
}

批處理作業排程

問題表述：給定n個作業的集合{J1,J2,…,Jn}。每個作業必須先由機器1處理，然後由機器2處理。作業Ji需要機器j的處理時間為tji。對於一個確定的作業排程，設Fji是作業i在機器j上完成處理的時間。所有作業在機器2上完成處理的時間和稱為該作業排程的完成時間和。

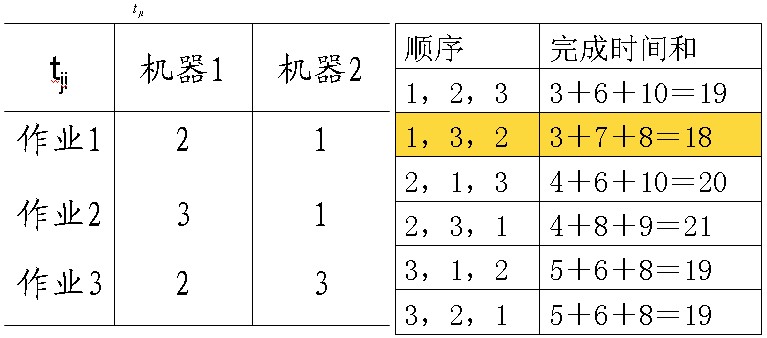
批處理作業排程問題要求對於給定的n個作業，制定最佳作業排程方案，使其完成時間和達到最小。

顯然，1,3,2是最佳排程方案。

解空間：排列樹（將作業順序進行全排列，分別算出各種情況的完成時間和，取最佳排程方案）

實現：

#include <iostream>
#include <vector>
using namespace std;

class flowshop 
{
public:
    flowshop(vector<vector<int> >& rhs) {
        task_count = rhs.size() ;
        each_t = rhs ;
        best_t.resize (task_count) ;
        machine2_t.resize (task_count,0) ; 
        machine1_t = 0 ;
        total_t = 0 ;
        best_total_t = 0 ;

        current_t.resize (task_count,0) ;
        for (int i = 0 ;i < task_count; ++ i) {
            current_t[i] = i; // 為了實現全排列
        }
    }
    void backtrack () {
        __backtrack (0);
        // 顯示最佳排程方案和最優完成時間和
        cout << "the best flowshop scheme is : ";
        copy (best_t.begin(),best_t.end(),ostream_iterator<int> (cout, " "));
        cout << endl;
        cout << "the best total time is : " << best_total_t << endl;
    }

private:
    void __backtrack (int i) {
        if (i >= task_count) {
            if (total_t < best_total_t || best_total_t == 0) {
                // 儲存當前最優排程方式
                copy (current_t.begin(),current_t.end(),best_t.begin()) ;
                best_total_t = total_t;
            }
            return ;
        }
        for (int j = i; j < task_count; ++ j) {
            // 機器1上結束的時間
            machine1_t += each_t[current_t[j]][0] ;
            if (i == 0) {
                machine2_t[i] = machine1_t + each_t[current_t[j]][1] ;
            }
            else {
                // 機器2上結束的時間
                machine2_t[i] = 
                    ((machine2_t[i - 1] > machine1_t) ? machine2_t[i - 1] : machine1_t)
                     + each_t[current_t[j]][1] ;
            }

            total_t += machine2_t[i];
            // 剪枝
            if (total_t < best_total_t || best_total_t == 0) {
                // 全排列
                swap (current_t[i],current_t[j]) ;
                __backtrack (i + 1) ;
                swap (current_t[i],current_t[j]) ;
            }

            machine1_t -= each_t[current_t[j]][0] ;
            total_t -= machine2_t[i] ;
        }
    }

public :
    int task_count ;        // 作業數
    vector<vector<int> >  each_t ;  // 各作業所需的處理時間
    vector<int> current_t ; // 當前作業排程
    vector<int> best_t ;        // 當前最優時間排程
    vector<int> machine2_t ;    // 機器2完成處理的時間
    int machine1_t ;        // 機器1完成處理的時間
    int total_t ;           // 完成時間和
    int best_total_t ;      // 當前最優完成時間和
};

int main()
{
    // const int task_count = 4;
    const int task_count = 3 ;
    vector<vector<int> > each_t(task_count) ;
    for (int i = 0;i < task_count; ++ i) {
        each_t[i].resize (2) ;
    }
    each_t[0][0] = 2 ;
    each_t[0][1] = 1 ;
    each_t[1][0] = 3 ;
    each_t[1][1] = 1 ;
    each_t[2][0] = 2 ;
    each_t[2][1] = 3 ;
    // each_t[3][0] = 1 ;
    // each_t[3][1] = 1 ;

    flowshop fs(each_t) ;
    fs.backtrack () ;
}

N後問題

問題表述：在n×n格的棋盤上放置彼此不受攻擊的n個皇后。按照國際象棋的規則，皇后可以攻擊與之處在同一行或同一列或同一斜線上的棋子。n後問題等價於在n×n格的棋盤上放置n個皇后，任何2個皇后不放在同一行或同一列或同一斜線上。求不同的解的個數。

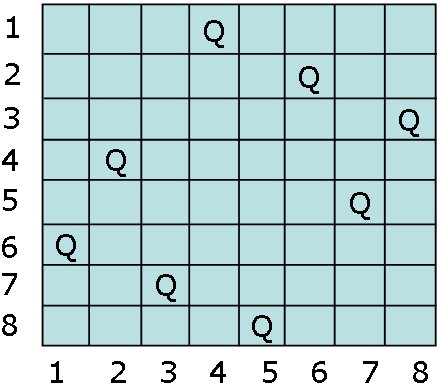
解向量：(x1, x2, … , xn)

顯約束：xi = 1,2, … ,n

隱約束：

1)不同列：xi != xj

2)不處於同一正、反對角線：|i-j| != |x(i)-x(j)|

解空間：滿N叉樹

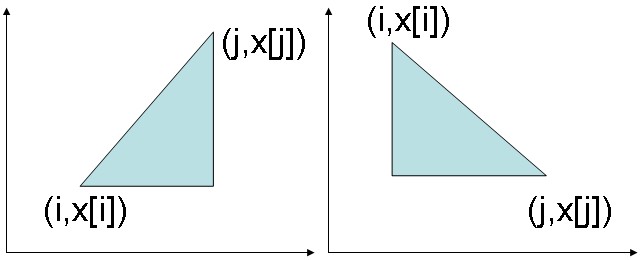
實現：

#include <iostream>
#include <vector>
using namespace std;

class queen
{
    // 皇后在棋盤上的位置
    struct q_place {
        int x;
        int y;
        q_place () 
            : x(0),y(0) 
        {}
    };

public:
    queen(int qc) 
    : q_count (qc), sum_solution (0) {
        curr_solution.resize (q_count);
    }

    void backtrack () {
        __backtrack (0);
    }

private:
    void __backtrack (int t) {
        if (t >= q_count) {
            // 找到一個解決方案
            ++ sum_solution ;
            for (size_t i = 0;i < curr_solution.size(); ++ i) {
                cout << "x = " << curr_solution[i].x 
                    << " y = " << curr_solution[i].y << endl;
            }
            cout << "sum_solution = " << sum_solution << endl;
        }
        else {
            for (int i = 0;i < q_count; ++ i) {
                curr_solution[t].x = i;
                curr_solution[t].y = t;
                if (__place(t)) {
                    __backtrack (t + 1);
                }
            }
        }
    }
    // 判斷第k個皇后的位置是否與前面的皇后相沖突
    bool __place (int k) {
        for (int i = 0; i < k; ++ i) {
            if ((abs(curr_solution[i].x - curr_solution[k].x) 
                == abs(curr_solution[i].y - curr_solution[k].y))
                || curr_solution[i].x == curr_solution[k].x) {
                return false;
            }
        }
        return true;
    }

private:
    vector<q_place> curr_solution;  // 當前解決方案
    const int q_count;              // 皇后個數
    int sum_solution;               // 當前找到的解決方案的個數
};

int main() 
{
    queen q(5);
    q.backtrack ();
    return 0;
}

旅行售貨員問題

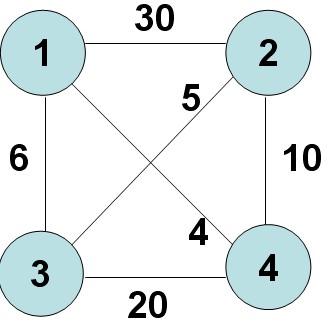
問題表述：在圖中找到一個權最小的周遊路線

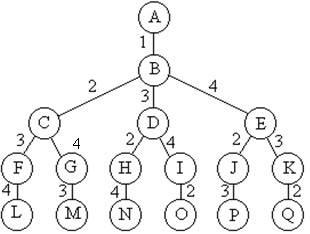
解空間：排列樹

剪枝策略：

當前路徑的權重＋下一個路徑的權重 < 當前的最小權重，則搜尋該路徑

實現：

#include <iostream>
#include <vector>
#include <iterator>
#include <algorithm>
using namespace std;

class traveling 
{

            
  
           

              
              
            
            
相關推薦
			   
            
            
            
 

    

    
    
演算法課堂實驗報告（五）——python回溯法與分支限界法（旅行商TSP問題）
     
 
                python實現回溯法與分支限界

一、開發環境

開發工具：jupyter notebook 並使用vscode，cmd命令列工具協助程式設計測試演算法,並使用codeblocks輔助編寫C++程式
程式語言：python3.6

二、實驗目標

1． 請用回溯法求對稱的旅 

  
 

    

    
    
回溯法與分支限界
     
 
							
							
							回溯法

1、有許多問題，當需要找出它的解集或者要求回答什麼解是滿足某些約束條件的最佳解時，往往要使用回溯法。 
2、回溯法的基本做法是搜尋，或是一種組織得井井有條的，能避免不必要搜尋的窮舉式搜尋法。這種方法適用於解一些組合數相當大的問題。 
3、回溯法在問題的 

  
 

    

    
    
六中常用演算法設計：窮舉法、分治法、動態規劃、貪心法、回溯法和分支限界法
     
 
								
								            
						
                演算法設計之六種常用演算法設計方法

1.直接遍歷態（窮舉法）

       程式執行狀態是可以遍歷的，遍歷演算法執行每一個狀態，最終會找到一個最優的可行解；適用於解決極小規模或者複雜度線性增長，而線 

  
 

    

    
    
常用演算法：分治演算法、動態規劃演算法、貪心演算法、回溯法、分支限界法
     
 
1、概念
    回溯演算法實際上一個類似列舉的搜尋嘗試過程，主要是在搜尋嘗試過程中尋找問題的解，當發現已不滿足求解條件時，就“回溯”返回，嘗試別的路徑。
   回溯法是一種選優搜尋法，按選優條件向前搜尋，以達到目標。但當探索到某一步時，發現原先選擇並不優或達不到目標，就退回一步重新選擇，這種走不通就退回再 

  
 

    

    
    
0/1揹包問題（回溯法、分支限界法、動態規劃法、貪心法）（C++版）
     
 
                此篇整理自李老師上課PPT           --- On one way by myself（1）問題描述    有n個重量分別為{w1，w2，…，wn}的物品，它們的價值分別為{v1，v2，…，vn}，給定一個容量為W的揹包。設計從這些物品中選取一部分物品放入該揹包的方 

  
 

    

    
    
分治法，動態規劃法，貪心法，回溯法，分支限界法的區別和聯絡以及適用情況
     
 
                    筆者這學期的《演算法設計與分析》課程已經進入尾聲，在這裡對學過的演算法進行總結歸納。筆者先對各個演算法的思想進行簡單的陳述，然後再進行對比。一、演算法思想    （一）分治法（divide and conquer method）    是將待求解的原問題劃分成k個較小 

  
 

    

    
    
資料結構與演算法- 五大常用演算法總結（分治法，回溯法，分治限界法，貪心演算法，動態規劃法）
     
  
 
 1.分治法（Recurrence and Divide-Conquer） 
        對於一個規模為n的問題，若該問題可以容易解決（比如說規模n較小）則直接解決，否則將其分解為k個規模較小的子問題，這些子問題互相獨立且與原問題形式相同，遞迴地解決這些子問 

  
 

    

    
    
0033演算法筆記——【分支限界法】分支限界法與單源最短路徑問題
     
 
                
      1、分支限界法
 (1)描述：採用廣度優先產生狀態空間樹的結點，並使用剪枝函式的方法稱為分枝限界法。
所謂“分支”是採用廣度優先的策略，依次生成擴充套件結點的所有分支（即：兒子結點）。所謂“限界”是在結點擴充套件過程中，計算結點的上界（或下界），邊搜尋邊減掉搜尋 

  
 

    

    
    
【基礎演算法】回溯法與八皇后問題
     
  
 
 #include"iostream"
#include"stdlib.h"
using namespace std;
int x[8],tot=0;
bool B(int x[],int k)
{
    int i;
    for(i=0;i<k;i++)
     if(x[i]==x[ 

  
 

    

    
    
回溯法與動態規劃例項分析
     
 
							
							
							回溯法與動態規劃
1、回溯法
1.1 適用場景
回溯法很適合解決迷宮及其類似的問題，可以看成是暴力解法的升級版，它從解決問題每一步的所有可能選項裡系統地選擇出一個可行的解決方案。回溯法非常適合由多個步驟組成的問題，並且每個問題都有多個選項。當我們從一步選擇了其中 

  
 

    

    
    
021-回溯法與深搜的關係-《演算法設計技巧與分析》M.H.A學習筆記
     
 
								
								            
						
                
關於回溯法與深搜的關係，一直沒有很好的搞明白，其實百度百科已經寫得很好了：

回溯法的基本思想：
在包含問題的所有解的解空間樹中，按照深度優先搜尋的策略，從根結點出發深度探索解空間樹。當探索到某一結點 

  
 

    

    
    
【LeetCode & 劍指offer刷題】回溯法與暴力列舉法題3：13 機器人的運動範圍
     
 【LeetCode & 劍指offer 刷題筆記】目錄（持續更新中...） 
13 機器人的運動範圍 
 
  
  題目描述 
  
   地上有一個m行和n列的方格。一個機器人
   從座標0,0的格子開始移動，每一次只能向左，右，上，下四個方向移動一格，但是
   不能進入行座標和列座 

  
 

    

    
    
【LeetCode & 劍指offer刷題】回溯法與暴力列舉法題4：Generate Parentheses
     
 【LeetCode & 劍指offer 刷題筆記】目錄（持續更新中...） 
Generate Parentheses 
 
  
   
    
    
     Given
      
     n
      
     pairs of parentheses, wr 

  
 

    

    
    
【LeetCode & 劍指offer刷題】回溯法與暴力列舉法題2：12 矩陣中的字串查詢（79. Word Search 系列）
     
 【LeetCode & 劍指offer 刷題筆記】目錄（持續更新中...） 
12 矩陣中的字串查詢（79. Word Search 系列） 
 
 
  Word Search
  
  
   
    
    
     Given a 2D board and a word, find if 

  
 

    

    
    
【LeetCode & 劍指offer刷題】回溯法與暴力列舉法題6：Number of Islands
     
 【LeetCode & 劍指offer 刷題筆記】目錄（持續更新中...） 
Number of Islands 
 
  
   
    
    
     Given a 2d grid map of
      
     '1'
     s (land) and
     &n 

  
 

    

    
    
【LeetCode & 劍指offer刷題】回溯法與暴力列舉法題7：Subsets（系列）
     
 【LeetCode & 劍指offer 刷題筆記】目錄（持續更新中...） 
Subsets 
 
  
   
    
    
     Given a set of
      
     distinct
      
     integers,
       

  
 

    

    
    
【LeetCode & 劍指offer刷題】回溯法與暴力列舉法題5：Letter Combinations of a Phone Number
     
 【LeetCode & 劍指offer 刷題筆記】目錄（持續更新中...） 
Letter Combinations of a Phone Number 
 
  
   
    
    
     Given a string containing digits from
       

  
 

    

    
    
回溯法與N皇后問題
     
 
							
							
							N皇后問題要求求解在N*N的棋盤上放置N個皇后，並使各皇后彼此不受攻擊的可能的棋盤佈局，皇后彼此不受攻擊的所有可能的佈局，皇后彼此不受攻擊的約束條件是：任何兩個皇后均不能在棋盤同一行、同一列或者在對角線上出現。

由於N皇后問題不允許兩個皇后在同一行，所以，可用 

  
 

    

    
    
五大常用演算法——分治法，動態規劃，回溯法，分支界限法，貪心演算法
     
 
                

分治演算法
一、基本概念

   在電腦科學中，分治法是一種很重要的演算法。字面上的解釋是“分而治之”，就是把一個複雜的問題分成兩個或更多的相同或相似的子問題，再把子問題分成更小的子問題……直到最後子問題可以簡單的直接求解，原問題的解即子問題的解的合併。這個技巧是很多高效 

  
 

    

    
    
回溯法與樹的遍歷
     
 
							
							
							關於回溯法和DFS做下總結: 
在程式設計中有一類題目求一組解或者求全部解或者求最優解等系列問題,不是根據某種特定的規則來計算,而是通過試探和回溯的搜尋來查詢結果,通常都會設計為遞迴形式.

這類題本身是一顆狀態樹,當只有兩種情況的時候則為二叉樹,這棵樹不是之前