資料結構例程——從根節點到每個葉子節點的路徑之逆
阿新 • • 發佈:2019-02-06
問題:設計演算法輸出從根節點到每個葉子節點的路徑之逆。
解法1:利用二叉樹後序遍歷非遞迴演算法中,每一個葉子節點出現時,棧中從棧頂到棧底,正好是葉子節點到根節點的逆序的性質編寫。
[參考解答](btreee.h見演算法庫)
#include <stdio.h>
#include "btree.h"
void AllPath1(BTNode *b)
{
BTNode *St[MaxSize];
BTNode *p;
int flag,i,top=-1; //棧指標置初值
if (b!=NULL)
{
do
{
while 解法2:利用二叉樹層次遍歷演算法的思路解決。
- 採用非環形順序佇列qu
- 層次遍歷二叉樹
- 將所有已訪問過的節點指標進隊,並在佇列中儲存雙親節點的位置。
- 當找到一個葉子節點時,在佇列中通過雙親節點的位置輸出根節點到該葉子節點的路徑之逆。
[參考解答](btreee.h見演算法庫)
#include <stdio.h>
#include "btree.h"
void AllPath2(BTNode *b)
{
struct snode
{
BTNode *node; //存放當前節點指標
int parent; //存放雙親節點在佇列中的位置
} qu[MaxSize]; //定義非環形佇列
BTNode *q;
int front,rear,p; //定義隊頭和隊尾指標
front=rear=-1; //置佇列為空佇列
rear++;
qu[rear].node=b; //根節點指標進入佇列
qu[rear].parent=-1; //根節點沒有雙親節點
while (front!=rear) //佇列不為空
{
front++; //front是當前節點*q在qu中的位置
q=qu[front].node; //隊頭出佇列,該節點指標仍在qu中
if (q->lchild==NULL && q->rchild==NULL)
{
p=front; //輸出*q到根節點的路徑序列
while (qu[p].parent!=-1)
{
printf("%c->",qu[p].node->data);
p=qu[p].parent;
}
printf("%c\n",qu[p].node->data);
}
if (q->lchild!=NULL) //*q節點有左孩子時將其進列
{
rear++;
qu[rear].node=q->lchild;
qu[rear].parent=front; //*q的雙親位置為front
}
if (q->rchild!=NULL) //*q節點有右孩子時將其進列
{
rear++;
qu[rear].node=q->rchild;
qu[rear].parent=front; //*q的雙親位置為front
}
}
}
int main()
{
BTNode *b;
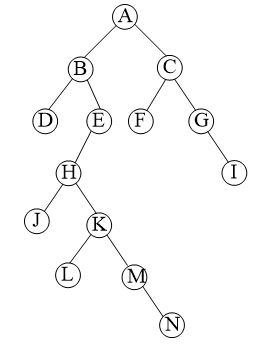
CreateBTNode(b,"A(B(D,E(H(J,K(L,M(,N))))),C(F,G(,I)))");
printf("二叉樹b: ");
DispBTNode(b);
printf("\n");
printf("從根節點到每個葉子節點的路徑之逆:\n");
AllPath2(b);
DestroyBTNode(b);
return 0;
}注:在main函式中,建立的用於測試的二叉樹如下——