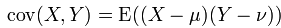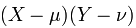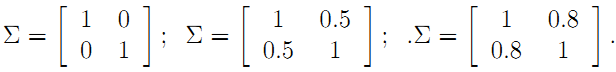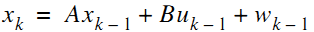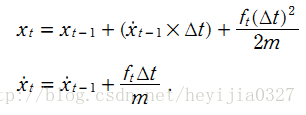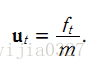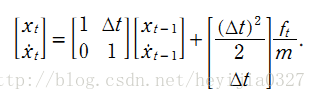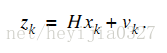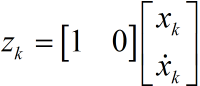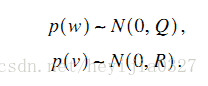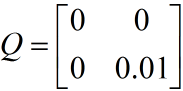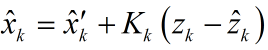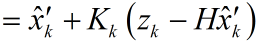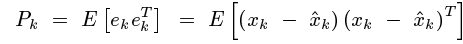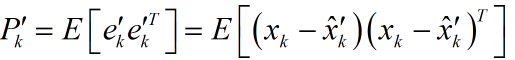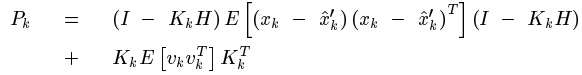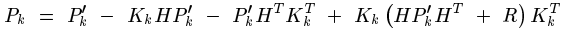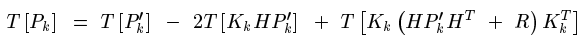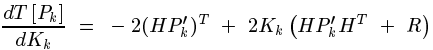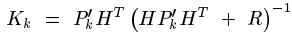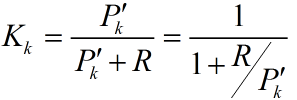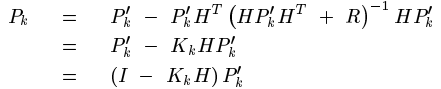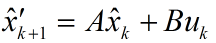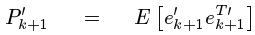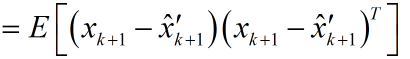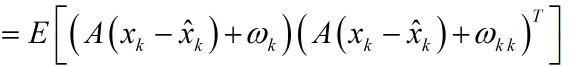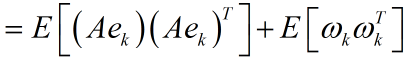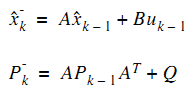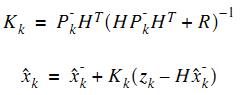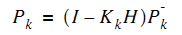卡爾曼濾波 -- 從推導到應用(一)
前言
卡爾曼濾波器是在估計線性系統狀態的過程中,以最小均方誤差為目的而推匯出的幾個遞推數學等式,也可以從貝葉斯推斷的角度來推導。
本文將分為兩部分:
第一部分,結合例子,從最小均方誤差的角度,直觀地介紹卡爾曼濾波的原理,並給出較為詳細的數學推導。
第二部分,通過兩個例子給出卡爾曼濾波的實際應用。其中將詳細介紹一個勻加速模型,並直觀的對比系統狀態模型的建立對濾波的影響。
第一部分
先看一個對理解卡爾曼濾波能起到作用的的笑話:
一片綠油油的草地上有一條曲折的小徑,通向一棵大樹.一個要求被提出:從起點沿著小徑走到樹下.
“很簡單.” A說,於是他絲毫不差地沿著小徑走到了樹下.
現在,難度被增加了:蒙上眼。
“也不難,我當過特種兵。” B說,於是他歪歪扭扭地走到了樹旁。“唉,好久不練,生疏了。” (只憑自己的預測能力)
“看我的,我有 DIY 的 GPS!” C說,於是他像個醉漢似地歪歪扭扭的走到了樹旁。“唉,這個 GPS 沒做好,漂移太大。”(只依靠外界有很大噪聲的測量)
“我來試試。” 旁邊一也當過特種兵的拿過 GPS, 蒙上眼,居然沿著小徑很順滑的走到了樹下。(自己能預測+測量結果的反饋)
“這麼厲害!你是什麼人?”“卡爾曼 ! ”
“卡爾曼?!你就是卡爾曼?”眾人大吃一驚。
“我是說這個 GPS 卡而慢。”
這個小笑話很有意思的指出了卡爾曼濾波的核心,預測+測量反饋,記住這種思想。
-----------------------------------------------------------分割線-----------------------------------------------------------------------
在介紹卡爾曼濾波前,簡單說明幾個在學卡爾曼過程中要用到的概念。即什麼是協方差,它有什麼含義,以及什麼叫最小均方誤差估計,什麼是多元高斯分佈。如果對這些有了瞭解,可以跳過,直接到下面的分割線。
均方誤差:它是"誤差"的平方的期望值(誤差就是每個估計值與真實值的差),也就是多個樣本的時候,均方誤差等於每個樣本的誤差平方再乘以該樣本出現的概率的和。
方差:方差是描述隨機變數的離散程度,是變數離期望值的距離。
注意兩者概念上稍有差別,當你的樣本期望值就是真實值時,兩者又完全相同。最小均方誤差估計就是指估計引數時要使得估計出來的模型和真實值之間的誤差平方期望值最小。
兩個實變數之間的協方差:
它表示的兩個變數之間的總體誤差,當Y=X的時候就是方差。下面說說我對協方差的通俗理解,先拋去公式中的期望不談,即假設樣本X,Y發生的概率就是1,那麼協方差的公式就變成了:
這就是兩個東西相乘,馬上聯想到數值影象裡的相關計算。如果兩個變數的變化趨勢一致,也就是說如果其中一個大於自身的期望值,另外一個也大於自身的期望值,那麼兩個變數之間的協方差就是正值。如果兩個變數的變化趨勢相反,即其中一個大於自身的期望值,另外一個卻小於自身的期望值,那麼兩個變數之間的協方差就是負值。協方差矩陣只不過就是元素多了組成了矩陣,其中協方差矩陣的對角線就是方差,具體公式形式請見wiki。
其實,這種相乘的形式也有點類似於向量投影,即兩個向量的內積。再遠一點,聯想到傅立葉變換裡頻譜系數的確定,要確定一個函式f(x)在某個頻率w上的頻譜,就是<f(x),cos(wt)>,< ,>表示向量內積,通俗的講是將f(x)投影到cos(wt)上,要講清傅立葉的本質需要另寫一篇博文,這裡提到這些只是覺得有益於對知識的相互理解。
高斯分佈:概率密度函式影象如下圖,四條曲線的方差各不相同,方差決定了曲線的胖瘦高矮。(圖片來源:維基百科)
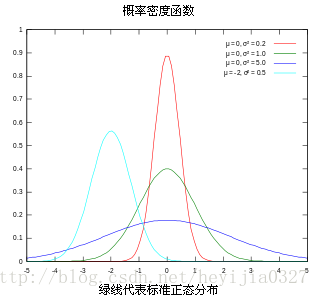
多元高斯分佈:就是高斯分佈的低維向高維的擴充套件,影象如下。
對應多元高斯分佈的公式也請自行谷歌,以前高斯公式中的方差也變成了協方差,對應上面三張圖的協方差矩陣分別如下:
注意協方差矩陣的主對角線就是方差,反對角線上的就是兩個變數間的協方差。就上面的二元高斯分佈而言,協方差越大,影象越扁,也就是說兩個維度之間越有聯絡。
-----------------------------------------------------------分割線---------------------------------------------------------------------
這部分每講一個數學性的東西,接著就會有相應的例子和直觀的分析幫助理解。
首先假設我們知道一個線性系統的狀態差分方程為
其中x是系統的狀態向量,大小為n*1列。A為轉換矩陣,大小為n*n。u為系統輸入,大小為k*1。B是將輸入轉換為狀態的矩陣,大小為n*k。隨機變數w為系統噪聲。注意這些矩陣的大小,它們與你實際程式設計密切相關。
看一個具體的勻加速運動的例項。
有一個勻加速運動的小車,它受到的合力為 ft , 由勻加速運動的位移和速度公式,能得到由 t-1 到 t 時刻的位移和速度變化公式:
該系統系統的狀態向量包括位移和速度,分別用 xt 和 xt的導數 表示。控制輸入變數為u,也就是加速度,於是有如下形式:
所以這個系統的狀態的方程為:
這裡對應的的矩陣A大小為 2*2 ,矩陣B大小為 2*1。
貌似有了這個模型就能完全估計系統狀態了,速度能計算出,位移也能計算出。那還要卡爾曼幹嘛,問題是很多實際系統複雜到根本就建不了模。並且,即使你建立了較為準確的模型,只要你在某一步有誤差,由遞推公式,很可能不斷將你的誤差放大A倍(A就是那個狀態轉換矩陣),以至於最後得到的估計結果完全不能用了。回到最開始的那個笑話,如果那個完全憑預測的特種兵在某一步偏離了正確的路徑,當他站在錯誤的路徑上(而他自己以為是正確的)做下一步預測時,肯定走的路徑也會錯了,到最後越走越偏。
既然如此,我們就引進反饋。從概率論貝葉斯模型的觀點來看前面預測的結果就是先驗,測量出的結果就是後驗。
測量值當然是由系統狀態變數映射出來的,方程形式如下:
注意Z是測量值,大小為m*1(不是n*1,也不是1*1,後面將說明),H也是狀態變數到測量的轉換矩陣。大小為m*n。隨機變數v是測量噪聲。
同時對於勻加速模型,假設下車是勻加速遠離我們,我們站在原點用超聲波儀器測量小車離我們的距離。
也就是測量值直接等於位移。可能又會問,為什麼不直接用測量值呢?測量值噪聲太大了,根本不能直接用它來進行計算。試想一個本來是朝著一個方向做勻加速運動的小車,你測出來的位移確是前後移動(噪聲影響),只根據測量的結果,你就以為車子一會往前開一會往後開。
對於狀態方程中的系統噪聲w和測量噪聲v,假設服從如下多元高斯分佈,並且w,v是相互獨立的。其中Q,R為噪聲變數的協方差矩陣。
看到這裡自然要提個問題,為什麼噪聲模型就得服從高斯分佈呢?請繼續往下看。
對於小車勻加速運動的的模型,假設系統的噪聲向量只存在速度分量上,且速度噪聲的方差是一個常量0.01,位移分量上的系統噪聲為0。測量值只有位移,它的協方差矩陣大小是1*1,就是測量噪聲的方差本身。
那麼:
Q中,疊加在速度上系統噪聲方差為0.01,位移上的為0,它們間協方差為0,即噪聲間沒有關聯。
理論預測(先驗)有了,測量值(後驗)也有了,那怎麼根據這兩者得到最優的估計值呢?首先想到的就是加權,或者稱之為反饋。
我們認定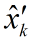
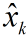
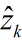
其中,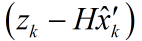
現在的關鍵就是求取這個K。這時最小均方誤差就起到了作用,順便在這裡回答為什麼噪聲必須服從高斯分佈,在進行引數估計的時候,估計的一種標準叫最大似然估計,它的核心思想就是你手裡的這些相互間獨立的樣本既然出現了,那就說明這些樣本概率的乘積應該最大(概率大才出現嘛)。如果樣本服從概率高斯分佈,對他們的概率乘積取對數ln後,你會發現函式形式將會變成一個常數加上樣本最小均方誤差的形式。因此,看似直觀上很容易理解的最小均方誤差理論上來源就出於那裡(詳細過程還請自行谷歌,請原諒,什麼都講的話就顯得這邊文章沒有主次了)。
先看估計值和真實值間誤差的協方差矩陣,提醒一下協方差矩陣的對角線元素就是方差,求這個協方差矩陣,就是為了利用他的對角線元素的和計算得到均方差.
這裡請注意ek是向量,它由各個系統狀態變數的誤差組成。如勻加速運動模型裡,ek便是由位移誤差和速度誤差,他們組成的協方差矩陣。表示如下:
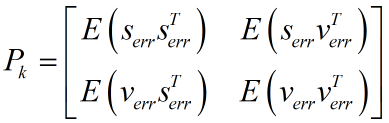
其中,Serr代表位移誤差,Verr代表速度誤差,對角線上就是各自的方差。
把前面得到的估計值代入這裡能夠化簡得:
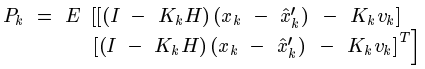
同理,能夠得到預測值和真實值之間誤差的協方差矩陣:
注意到系統狀態x變數和測量噪聲之間是相互獨立的。於是展開(1)式可得:
最後得到:
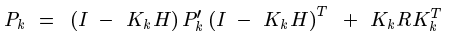
繼續展開:
接下來最小均方差開始正式登場了,回憶之前提到的,協方差矩陣的對角線元素就是方差。這樣一來,把矩陣P的對角線元素求和,用字母T來表示這種運算元,他的學名叫矩陣的跡。
最小均方差就是使得上式最小,對未知量K求導,令導函式等於0,就能找到K的值。
注意這個計算式K,轉換矩陣H式常數,測量噪聲協方差R也是常數。因此K的大小將與預測值的誤差協方差有關。不妨進一步假設,上面式子中的矩陣維數都是1*1大小的,並假設H=1,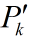
所以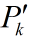
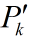
將計算出的這個K反代入Pk中,就能簡化Pk,估計協方差矩陣Pk的:
因此遞推公式中每一步的K就計算出來了,同時每一步的估計協方差也能計算出來。但K的公式中好像又多了一個我們還未曾計算出來的東西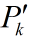
請先注意到預測值的遞推形式是:
由於系統狀態變數和噪聲之間是獨立,故可以寫成:
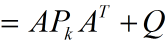
由此也得到了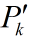
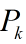
這裡總結下遞推的過程,理一下思路:
首先要計算預測值、預測值和真實值之間誤差協方差矩陣。
有了這兩個就能計算卡爾曼增益K,再然後得到估計值,
最後還要計算估計值和真實值之間的誤差協方差矩陣,為下次遞推做準備。
至此,卡爾曼濾波的理論推導到此結束。還有一些如實際應用中狀態方程建立不正確,預測結果會怎樣等這樣的細節問題,以及一些總結留到第二部分討論。
reference:
1.Greg Welch & Gary Bishop. << An Introduction to the Kalman Filter >>
2.Tony Lacey. << Tutorial:The Kalman Filter >>.
3.Ramsey Faragher. << Understanding the Basis of the Kalman Filter Via a Simple and Intuitive Derivation >>
5.很多概念定義來自維基百科