前面在逆分佈函式法生成隨機數（以指數分佈和雙指數分佈為例）中已經說道了逆分佈函式方法生成隨機數，理論上來說的話，對於任意的分佈都是可以用逆分佈函式的方法得到的，因為分佈函式都是單調函式，也就是是說是可逆的，當然除了一些非常極端的情況，例如，函式雖然是遞增的但是在某一段為常數，這時候求逆函式的話會面臨一對多的情況，不過這裡需要與離散的情況分開，離散的時候，分佈函式是階梯函式，此時其逆函式就會出現一對多的情況，但是由於已經知道了它取的是離散值，那麼此時只需要取多個值中的一個（例如區間的左端點或右端點）。

       但是有的情況使用逆分佈函式是不方便的，例如我們最常用的正態分佈，其分佈函式為（這裡說的是標準正態分佈，其他的正態分佈可直接由標準正態分佈得到）：

       沒有顯式表示式，所以更別說是求得其逆函數了，那麼這時候有什麼辦法可以解決呢？這裡來看一下非常有名的接受/拒絕方法（acceptance/rejection method),其演算法步驟如下：

        假設：為需要生成的隨機數的密度函式，這裡就對應為上面積分號中的部分，又設另外一個容易取樣的隨機變數（如前面提到的：指數分佈和雙指數分佈）的密度函式為，且存在常數c使得成立的話，那麼有如下的演算法：

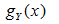
注：其中的g 也叫做majoring function 

這裡需要注意的有：

1）此處的c雖然可以任意的取，但是c太大的話成功生成服從的隨機數的所需的次數會很多，其實可以證明成功的次數服從均值為c的幾何分佈，所以c 的選取是需要考慮的一個問題。

2）從1）還可得到的是作為majoring function的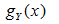的形狀與越接近越好，所以下面用Double Exponent 分佈作為標準正態分佈的majoring function

3）支撐集至少包含的定義域，這裡是因為如果分母為0的話，那個不等式是不可能成立的（支撐集，就是函式值不為0的所有點的集合）

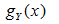
2）此處的 X 和 y可以是多維的，也就是可以產生多維的分佈，下面描述了該框架下二維情況：

下面給出上述演算法的一個簡單證明：

這裡解釋一下：第一行利用了條件概率公式的定義，第二行只是把它展開，其中的就是示性函式，第三行的最後一步是因為，分母是密度函式的積分，所以他就等於1，最後一行就是分佈函式的定義。

到此，理論部分就基本結束了，下面來看看用acceptance/rejection method 產生正態分佈的隨機數。

首先估計引數c：

我們有：

計算可知上面的最大值為：

為了保險起見這裡取c=1.5，帶入前面的演算法就可以生成標準正態分佈的隨機數了：

下面是我寫的程式碼，注意這裡沒有列出unform()的生成程式碼，原因均勻分佈的實現較簡單，前面在C++均勻分佈U(0,1)的隨機數中已經有介紹；這裡使用英文註釋是因為輸入法之間的切換太麻煩，可能有需要商榷的地方，希望諒解。

double RandNum::Dexponent(double a,double b)
{// generate a random number subject to double exponent distribute
	double u=uniform();
	if(u<0.5)
	  return a+b*log(2*u);
	else
	  return a-b*log(2*(1-u));
}
double RandNum::normal()
{// generate a random number subject to normal distribution 
	double PI=3.1415926;
	double c=1.5; // set the const 'c' as 1.5
	double y=Dexponent(0,1);
	double fy=(1.0/sqrt(2*PI))*exp(-y*y/2);
	double gy=(1.0/2.0)*exp(-abs(y));
	double r=fy/(c*gy);
	double u=uniform();
	while(u>r)// reject
	{
		y=Dexponent(0,1);
		fy=(1.0/sqrt(2*PI))*exp(-y*y/2);
		gy=(1.0/2.0)*exp(-abs(y));
		r=fy/(c*gy);
		u=uniform();
	}
	return y; // accepte
}

最後，還要提的是，實際中生成標準正態分佈的隨機數可能還是逆分佈函式法，雖然其分佈函式求不出來，但是，換個角度我們可以將：

看作是變上限積分，解決積分問題，學過數值計算的人都知道，一個好一點的演算法就可以達到很高的精度，所以通過數值計算也會很方便而且精度也很高，這裡我就不細說了，因為我還沒有實踐過，故而沒有發言權。

        這時候，可能有人會說，逆著不是坑我嗎？實際中不這樣用逆=你不早說，我都看到這裡了你才說；不過請注意這裡的主要目的是介紹演算法，生成標準正態分佈只是為了加深演算法印象的，概演算法並不是專門用來生成標準正態分佈的，其他地方也可以用。