弗羅萊演算法是生成歐拉回路的演算法之一，今天查看了許多資料，做一下記錄整理。

1、關於尤拉圖：

              尤拉圖是由哥尼斯堡橋問題抽象而來的。哥尼斯堡橋問題是指在Pregel河兩岸就7座橋，問能否一次走完所有的橋並且不重複。問題如下：

              將問題抽象後可以變為圖問題。尤拉將此問題解決。所以稱這種能遍歷所有邊且每條邊至多且必須出現一次的圖為尤拉圖。稱這種封閉路徑為歐拉回路（此問題也稱為一筆畫問題）。

2、歐拉回路存在的充分必要條件：

               給定一個無向連通圖G=（V，E），其所有頂點的度為偶數   <=======>   此圖是無向連通圖。

               證明過程不難，此處省略。

3、歐拉回路的生成演算法：

               生成歐拉回路的演算法應該會有很多。在參考的離散數學資料中，有根據尤拉圖證明過程生成歐拉回路的演算法。此處給出演算法的大體思想。

               演算法一：a：在圖G中選擇一個頂點作為起點，記為H。並將歐拉回路記做P，初始的歐拉回路只有H，並記做V（P） = {H}

                               b：在V（P）中選擇任一頂點記為W，若W與V（G）-V（P）的點相關聯，則擴充套件一條W-W的迴路C，將路徑記為P'---W----C-----W-----P''。

                               c：重複b直至P中包含所有邊為止。

               演算法二：主要講fleury演算法。演算法的思想為

任取v0∈V(G)，令P0=v0；
設Pi=v0e1v1e2…ei vi已經行遍，按下面方法從中選取ei+1：
（a）ei+1與vi相關聯；
（b）除非無別的邊可供行遍，否則ei+1不應該為Gi=G-{e1,e2, …, ei}中的橋（所謂橋是一條刪除後使連通圖不再連通的邊）；
（c）當（b）不能再進行時，演算法停止。

public void euler(int[][] graph,Stack s,int current,int start){
		int num_edges;  //graph中的邊數
		boolean flag = false;  //是否還有與x關聯的邊
		s.push(current);
		for(int i = start; i < graph.length ; i++){
			//從start開始搜尋是否有邊
			if(graph[i][x] > 0){ //i與current有邊
				flag = true;
				graph[i][current] = 0; graph[current][i] = 0; //刪除邊
				euler(graph,s,i,0);  //從i開始搜尋
				break;
			}
		}
		
		if(flag){ //如果沒有變與當前節點current相連
			s.pop();
			int m = s.peek();
			G[m][current] = G[current][m] = 1; //恢復邊
			int new_start = current + 1;
			if(s.size() == num_edges){ //完成迴路
				return;
			}else{
				euler(graph,s,m,new_start);
			}
		}
 

4、例子：

（圖片節選自外部，如有侵權，請聯絡）

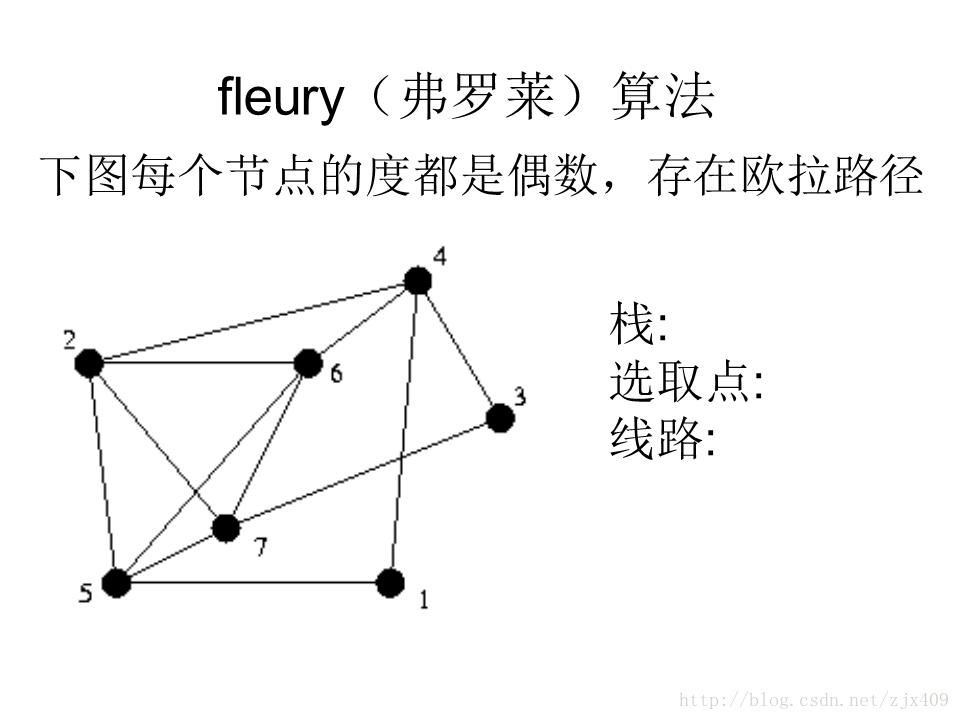
按照演算法的歐拉回路為

1---5--- 7--- 6--- 4--- 3--- 7--- 2--- 6--- 5--- 2--- 4--- 1