佛羅萊(Fleury)演算法
今天被這個叫Fleury演算法的東西折磨了一下午,這個演算法是解決歐拉回路問題的,其實已經被歐拉回路折磨兩天了。
圖論這本書本是打算一個寒假解決掉的,最初的時候認為會卡到第六章網路流部分,沒想到在第五章可行性遍歷就卡了。
首先是尤拉圖,然後就是DFS解決尤拉圖順序問題,今天又卡到了佛羅萊演算法,簡直了。
佛羅萊演算法是用來求歐拉回路的,判斷歐拉回路十分簡單,但是求歐拉回路一般是用DFS解決,但是DFS時間複雜度有些高,而佛羅萊演算法能把時間複雜度壓縮到O(e * e),e是邊的數量。
原理:
任取v0∈V(G),令P0=v0;
設Pi=v0e1v1e2…ei vi已經行遍,按下面方法從中選取ei+1:
(a)ei+1與vi相關聯;
(b)除非無別的邊可供行遍,否則ei+1不應該為Gi=G-{e1,e2, …, ei}中的橋(所謂橋是一條刪除後使連通圖不再連通的邊);
(c)當(b)不能再進行時,演算法停止。
可以證明,當演算法停止時所得的簡單迴路Wm=v0e1v1e2….emvm(vm=v0)為G中的一條歐拉回路。
當然,這個“可以證明”我還暫時證明不出來= =。
佛羅萊演算法還是使用了DFS,其中這DFS的目的在於找出“橋”,當刪掉一些邊後整個圖不連通,而最後刪掉恰好不連通的那個邊正是橋。
然後遇到橋之後棧回退不走橋(保證為走過的圖還是連通)然後選擇其他非橋的路進行繼續入棧儲存並繼續DFS刪邊找橋。
有一點需要注意,就是棧裡儲存了什麼,開始的時候我以為是路線,所以對這個演算法一直想不明白,就在剛才我突然想到,我們找的是歐拉回路,也就是說起點就是終點,而對於橋的兩個點都是兩個迴路,我們大可放心把橋的一段壓在棧裡不列印而繼續都是把橋的另一端搜尋完再列印,效果是一樣的。
比如圖:

如果以2開始,進行2 3 4 5 3 2 8 2的順序進行遍歷,在8到2的時候進入了死衚衕,正是因為在8的時候進入橋(e9讓2和其他結點斷開)
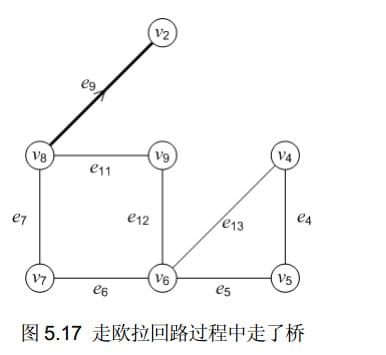
如果在8的時候轉向,開始9或7的繼續遍歷邊解決這個問題,但是我的疑惑便是,因為剛開始的遍歷到8為止,所有路線都儲存在棧裡,而退出的過程需要列印8,也就是說列印完8之後就不管之前入棧的結點而繼續向下遍歷,為什麼還能保證正確。
因為8換方向遍歷然後入棧的依然是(子圖的)歐拉回路,也定將以8結束來上(剛才留下的)橋進行最後的遍歷。而所謂的最後遍歷也就是剛才已經留在棧中的結點。
因此棧是儲存的路徑但不是遍歷路徑而是儲存了一個保證正確但不保證和遍歷順序相同的路徑(在遇到橋的時候可能會導致最後退棧逆序)。
Fleury實現:
#include <iostream>
#include <math.h>
#include <algorithm>
#include <cstring>
#include <stack>
#define INF 100000
using namespace std;
int G[100][100];
int n;
stack<int> s;
void dfs(int x)
{
s.push(x);
for(int i = 1; i <= n; i++)
{
if(G[i][x] > 0)
{
G[x][i] = 0;
G[i][x] = 0;
dfs(i);
break;
}
}
}
void fleury(int x)
{
int b;
s.push(x);
while(!s.empty())
{
b = 0;
for(int i = 1; i <= n; i++)
{
if(G[s.top()][i] > 0)
{
b = 1;
break;
}
}
if(b == 0)
{
cout << s.top() << " ";
s.pop();
}
else
{
int t = s.top();
s.pop();
dfs(t);
}
}
}
int main()
{
int m;
while(cin >> n >> m,n)
{
while(!s.empty())
s.pop();
memset(G,0,sizeof(G));
for(int i = 0; i < m; i++)
{
int a,b;
cin >> a >> b;
G[a][b] = 1;
G[b][a] = 1;
}
int num = 0;
int start = 2;
for(int i = 1; i <= n; i++)
{
int d = 0;
for(int j = 1; j <= n; j++)
d += G[i][j];
if(d % 2 == 1)
{
start = i;
num++;
}
}
if(num == 0 || num == 2)
fleury(start);
else
cout << "No Euler path" << endl;
}
return 0;
}

歡迎到微信裡去當吃瓜群眾
