基本演算法_堆排序_Java實現
阿新 • • 發佈:2019-02-07
1.堆排序
堆排序就是將序列調整為指定的堆,然後調整首尾元素的位置,取出末尾元素,反覆進行,直到將所有元素取出,形成一個有序的序列。假設存在n個元素的序列
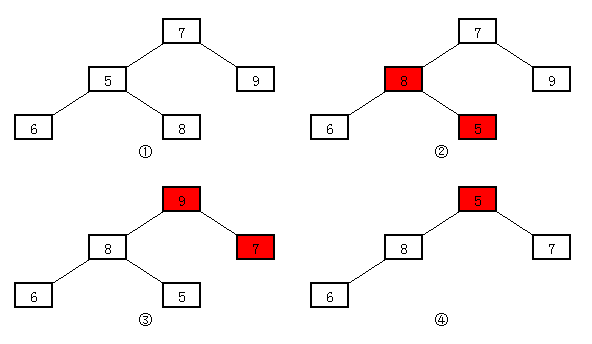
存在一個序列【7】【5】【9】【6】【8】,按照從小到大的順序進行排序。
①將無序序列構造成一個堆。
②取出子節點中6和8較大的值,與父節點5進行比較,比父節點5大,則交換位置。
③取出子節點中8和9較大的值,與根節點7進行比較,比跟節點7大,則交換位置,此時序列已調整為大根堆。
④將節點9和5調換位置,同時取出節點9,然後按照相同的方式將序列轉換為大根堆,取出序列中最大的數,重複操作直到序列中所有數取出完畢,生成一個新的有序序列。
2.示例程式碼
存在一個序列N由小到大進行排序,將序列轉換為大根堆,交換首尾元素的位置,再將子序列N-1轉換為大根堆,交換收尾元素位置,反覆進行,當子序列剩餘一個元素時,此時的序列為一個有序序列。
public class HeapSort { public static void main(String[] args) { int[] array = { 9, 8, 7, 6, 5, 4, 3, 2, 1, 0 }; HeapSort.sort(array); System.out.println("排序後陣列:" + Arrays.toString(array)); } public static void sort(int[] a) { // 迴圈建立初始堆,若父節點索引為i,那麼左節點的索引為i*2+1,即左節點為a.length時,其父節點應當小於a.length/2 for (int i = a.length / 2; i >= 0; i--) {// 遍歷存在子節點的父節點 adjustHeap(a, i, a.length - 1); } // 進行n-1次迴圈完成排序 for (int i = a.length - 1; i > 0; i--) { // 最後一個元素和第一個元素進行交換 int temp = a[i]; a[i] = a[0]; a[0] = temp; adjustHeap(a, 0, i); } } // 將陣列轉換為大根堆,大根堆的根節點為陣列中的最大值 public static void adjustHeap(int[] a, int parent, int length) { int temp = a[parent]; // 父節點的值 int child = 2 * parent + 1; // 左子節點的索引 while (child < length) {// 判斷左節點是否為最大索引 // 如果有右孩子結點,並且右孩子結點的值大於左孩子結點,則選取右孩子結點 if (child + 1 < length && a[child] < a[child + 1]) { child ++;// 將左子節點轉換為右子節點 } // 當父節點的值直接大於子節點的值時,直接退出 if (temp > a[child]) break; // 將子節點的值賦值給父節點 a[parent] = a[child]; // 選取子節點的左子節點繼續向下篩選 parent = child; child = 2 * parent + 1; } // 若發生交換,此時parent代表子節點索引,沒有發生交換,此時parent仍舊代表父節點索引 a[parent] = temp; } }
3.演算法分析
時間複雜度:堆排序的時間複雜度為
演算法穩定性:排序前後相同元素間的相對位置可能會發生改變,堆排序是一種不穩定的排序演算法。
