排序演算法1——圖解氣泡排序及其實現（三種方法，基於模板及函式指標）
排序演算法2——圖解簡單選擇排序及其實現
排序演算法3——圖解直接插入排序以及折半（二分）插入排序及其實現
排序演算法4——圖解希爾排序及其實現
排序演算法5——圖解堆排序及其實現
排序演算法6——圖解歸併排序及其遞迴與非遞迴實現
排序演算法7——圖解快速排序以及不同CUTOFF的時間測試

堆的概念和性質

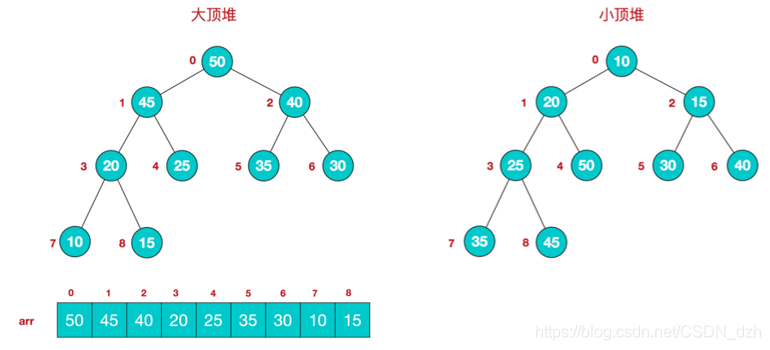
堆，是一種特殊的二叉樹，每個子結點的值總是小於（或者大於）它的父結點，相應的分為最大堆和最小堆

堆，是一個完全二叉樹，一般情況下堆排序都是用陣列的方式實現

這裡可以看到，若以0開始編號

大頂堆：arr[i] >= arr[2i+1] && arr[i] >= arr[2i+2]
小頂堆：arr[i] <= arr[2i+1] && arr[i] <= arr[2i+2]

下面的性質是最重要的：
若以0開始編號，對編號為 i 的結點，其左孩子為2i+1，右孩子為2i+2，二者相差為1
第一個非葉子結點編號為(int)(length/2)-1
最後一個結點的編號為length-1

堆排序的基本思想

利用最大堆（對應升序）或者最小堆（對應降序）輸出堆頂元素，即最大值（或最小值），
然後將剩下元素重新生成最大堆（或者最小堆），繼續輸出堆頂元素，重複此過程直到全部元素都已輸出即可得到有序序列

空間複雜度為O（N）的方法

額外開闢一個輔助的陣列空間，將堆頂元素逐一放入輔助數組裡，最後再把輔助陣列的內容賦值回原始的陣列

空間複雜度為O（1）的方法

這個方法的時間複雜度與前一種相同，都是O（NlogN），但是不需要額外的輔助陣列，所以空間複雜度為O（1）
但堆排序是不穩定排序

主要的步驟是：
1.先將一個無序的序列生成一個最大堆
2.將堆頂元素與堆的最後一個元素對換位置
3.將剩餘的元素重新生成一個最大堆
4.重複2-3步驟，直到堆中只剩一個元素

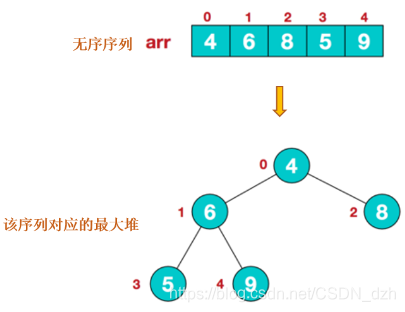
首先介紹給出一個待排序的無序序列，並以完全二叉樹的形式將其繪製出來

可以看到，該無序序列並不是一個最大堆

於是，做上述步驟的第一步，我們將其變為一個最大堆
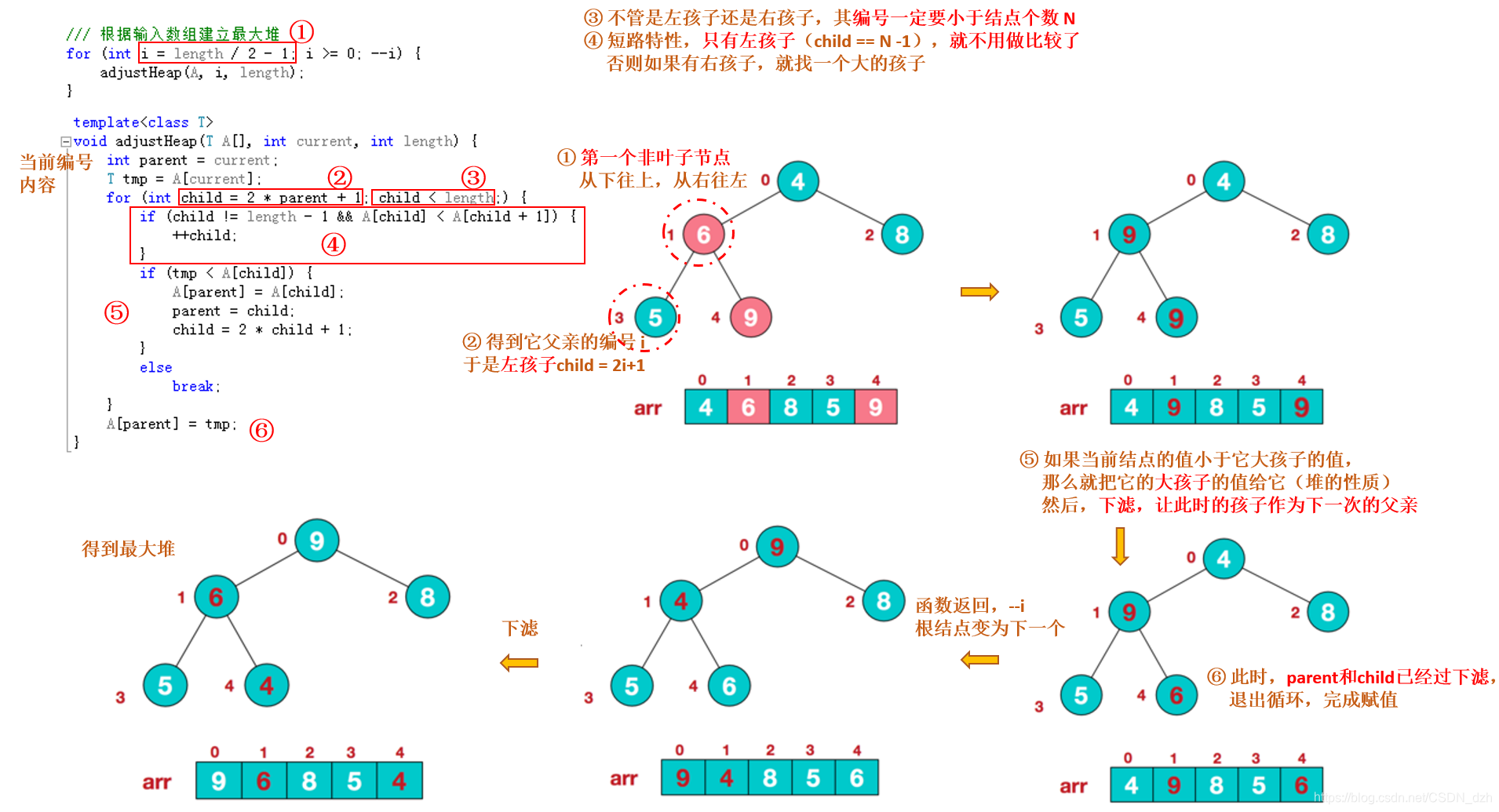
那麼，怎麼變呢？我們需要從第一個非葉子節點開始，也就是編號為length/2-1的那個結點
針對上面的例子，length/2-1也就是5/2-1=1了
下面，一圖帶你讀懂最大堆的構建

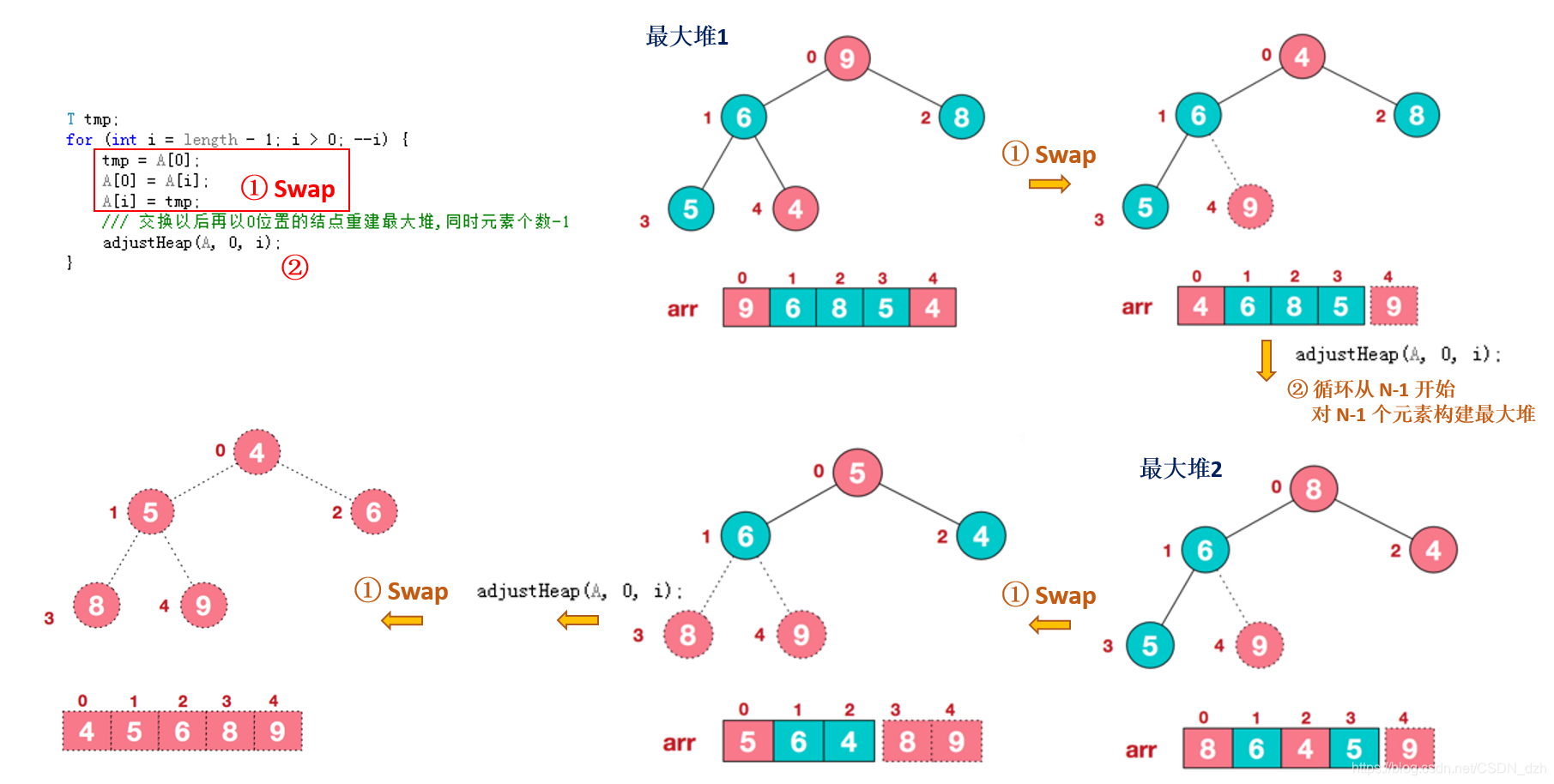
下面，我們執行上述的步驟2和步驟3
2.將堆頂元素與堆的最後一個元素對換位置
3.將剩餘的元素重新生成一個最大堆

從上面可以看到，堆排序的整體主要由兩部分組成
1.構建初始堆，時間複雜度為O（N）
2.交換堆頂和末尾元素並對剩餘元素重建最大堆，重建堆的時間複雜度為O（NlogN）

所以總體來說，堆排序的時間複雜度為O（NlogN）
它對原始記錄的排序狀態並不敏感，最好最壞和平均時間複雜度都是O（NlogN）
在空間上，只有一個用來交換的暫存單元，空間複雜度也很好
由於記錄的比較與交換是跳躍式進行，因此也是不穩定的。

由於初始構建所需的比較次數較多，因此不適合待排序序列較少的情況

測試結果及程式碼

#include <iostream>

template<class T>
void adjustHeap(T A[], int current, int length) {
	int parent = current;
	T tmp = A[current];
	for (int child = 2 * parent + 1; child < length;) {
		if (child != length - 1 && A[child] < A[child + 1]) {
			++child;
		}
		if (tmp < A[child]) {
			A[parent] = A[child];
			parent = child;
			child = 2 * child + 1;
		}
		else
			break;
	}
	A[parent] = tmp;
}

template<class T>
void HeapSort(T A[], int length) {
	/// 根據輸入陣列建立最大堆
	for (int i = length / 2 - 1; i >= 0; --i) {
		adjustHeap(A, i, length);
	}

	T tmp;
	for (int i = length - 1; i > 0; --i) {
		tmp = A[0];
		A[0] = A[i];
		A[i] = tmp;
		/// 交換以後再以0位置的結點重建最大堆,同時元素個數-1
		adjustHeap(A, 0, i);
	}

}

template<class T>
void ArrShow(T *A, int length) {
	for (int i = 0; i < length; ++i) {
		std::cout << A[i] << " ";
	}
	puts("\n");
}

int main(int argc, char *argv[]) {
	int test[9] = { 1, 2, 7, 3, 4, 6, 8, 5, 9 };
	ArrShow(test, 9);

	puts("HeapSort : ");
	HeapSort(test, 9);
	ArrShow(test, 9);


	return 0;
}