以下程式碼來自Deep Learning for Computer Vision with Python第九章。

一、梯度下降法（Gradient Decent）

# import the necessary packages
from sklearn.model_selection import train_test_split
from sklearn.metrics import classification_report
from sklearn.datasets import make_blobs
import matplotlib.pyplot as plt
import numpy as np
import argparse

def sigmoid_activation(x):
	# compute the sigmoid activation value for a given input
	return 1.0 / (1 + np.exp(-x))

def predict(X, W):
	# take the dot product between our features and weight matrix
	preds = sigmoid_activation(X.dot(W))
	
	# apply a step function to threshold the outputs to binary
	# class labels
	preds[preds <= 0.5] = 0
	preds[preds > 0] = 1

	# return the predictions
	return preds
	
# construct the argument parse and parse the arguments
ap = argparse.ArgumentParser()
ap.add_argument("-e", "--epochs", type=float, default=100,
	help="# of epochs")
ap.add_argument("-a", "--alpha", type=float, default=0.01,
	help="learning rate")
args = vars(ap.parse_args())

# generate a 2-class classification problem with 1,000 data points,
# where each data point is a 2D feature vector
(X, y) = make_blobs(n_samples=1000, n_features=2, centers=2,
	cluster_std=1.5, random_state=1)
y = y.reshape((y.shape[0], 1))

# insert a column of 1's as the last entry in the feature
# matrix -- this little trick allows us to treat the bias
# as a trainable parameter within the weight matrix
X = np.c_[X, np.ones((X.shape[0]))]

# partition the data into training and testing splits using 50% of
# the data for training and the remaining 50% for testing
(trainX, testX, trainY, testY) = train_test_split(X, y,
	test_size=0.5, random_state=42)
	
# initialize our weight matrix and list of losses
print("[INFO] training...")
W = np.random.randn(X.shape[1], 1)
losses = []

# loop over the desired number of epochs
for epoch in np.arange(0, args["epochs"]):
	# take the dot product between our features 'X' and the weight
	# matrix 'W', then pass this value through our sigmoid activation
	# function, thereby giving us our predictions on the dataset
	preds = sigmoid_activation(trainX.dot(W))

	# now that we have our predictions, we need to determine the
	# 'error', which is the difference between our predictions and
	# the true values
	error = preds - trainY
	loss = np.sum(error ** 2)
	losses.append(loss)

	# the gradient descent update is the dot product between our
	# features and the error of the predictions
	gradient = trainX.T.dot(error)

	# in the update stage, all we need to do is "nudge" the weight
	# matrix in the negative direction of the gradient (hence the
	# term "gradient descent" by taking a small step towards a set
	# of "more optimal" parameters
	W += -args["alpha"] * gradient

	# check to see if an update should be displayed
	if epoch == 0 or (epoch + 1) % 5 == 0:
		print("[INFO] epoch={}, loss={:.7f}".format(int(epoch + 1),
			loss))
			
# evaluate our model
print("[INFO] evaluating...")
preds = predict(testX, W)
print(classification_report(testY, preds))

# plot the (testing) classification data
plt.style.use("ggplot")
plt.figure()
plt.title("Data")
plt.scatter(testX[:, 0], testX[:, 1], marker="o", c=testY, s=30)

# construct a figure that plots the loss over time
plt.style.use("ggplot")
plt.figure()
plt.plot(np.arange(0, args["epochs"]), losses)
plt.title("Training Loss")
plt.xlabel("Epoch #")
plt.ylabel("Loss")
plt.show()

 

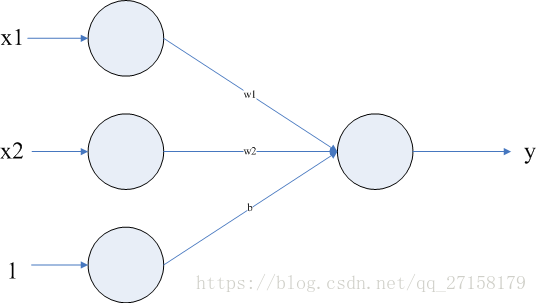
本例子的神經網路是隻有兩層，輸入3，輸出1，（3-1）。且輸入3個神經元中，最後一個是輸入為1。是為了將偏移(bias)b值放到權重矩陣W中。

Python語言，使用了sklearn、matplotlib、numpy、imutils這幾個庫。

這個例程中，學習的內容如下：

1、細胞元啟用函式

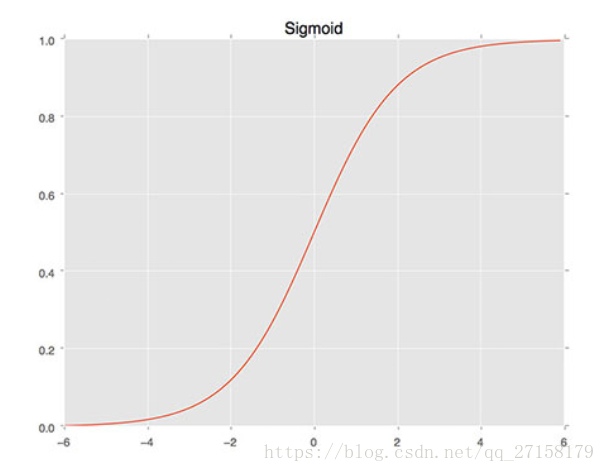
本例子採用sigmoid函式。

sigmoid函式曲線如下：

理論上，神經網路中每個神經元只有兩種狀態：有反應、無反應，即1和0。但這裡允許神經元具有0-1V之間的任意電壓。且輸入輸出符合Sigmoid曲線。

2、predict預測函式

預測函式中，把輸入的變數X（3行1列矩陣）經過轉置變成1行3列，乘以權值W（3行1列），得到輸出。

3、網路初始化

使用make_blobs函式生成了1000個樣品，每個樣品兩個引數。即輸入矩陣是1000行2列。輸出只有一個引數，是1行1000列。

X = np.c_[X, np.ones((X.shape[0]))]這語句可以在輸入矩陣最低加上一行1，同時把權值W（weights）矩陣初始化為3行1列，最後1列是偏置b（bias）。

線性分類基本公式是：

可以把b放進權重W矩陣的最後一行，這樣的好處是，可以在訓練W矩陣時，也訓練了b引數。

train_test_split函式可以將樣品（X,y）按比例分配成一部分用於訓練，一部分用於測試。

4、網路訓練

這例子，更新權重矩陣W的頻率是把全部訓練樣品處理一次，才更新一次的權重。因此學習速度十分緩慢。

error是全部訓練樣品的預測結果，和實際結果y想減。

損失函式是error中每個元素的平方和：loss = np.sum(error ** 2) 

更新權值的公式是

error = preds - trainY

gradient = trainX.T.dot(error)

W += -args["alpha"] * gradient

5、網路測試
測試使用了classification_report.第一個引數是實際值，第二個引數是預測值。報告可自動生成精度、測試樣品數量。
print(classification_report(testY, predict(testX, W)))

6、檔案執行結果

========= RESTART: E:\FENG\workspace_python\ch9_gradient_descent.py =========
[INFO] training...
[INFO] epoch=1, loss=155.6216601
[INFO] epoch=5, loss=0.1092728
[INFO] epoch=10, loss=0.1032095
[INFO] epoch=15, loss=0.0976591
[INFO] epoch=20, loss=0.0925605
[INFO] epoch=25, loss=0.0878624
[INFO] epoch=30, loss=0.0835212
[INFO] epoch=35, loss=0.0794996
[INFO] epoch=40, loss=0.0757656
[INFO] epoch=45, loss=0.0722911
[INFO] epoch=50, loss=0.0690518
[INFO] epoch=55, loss=0.0660262
[INFO] epoch=60, loss=0.0631954
[INFO] epoch=65, loss=0.0605427
[INFO] epoch=70, loss=0.0580530
[INFO] epoch=75, loss=0.0557131
[INFO] epoch=80, loss=0.0535110
[INFO] epoch=85, loss=0.0514360
[INFO] epoch=90, loss=0.0494784
[INFO] epoch=95, loss=0.0476294
[INFO] epoch=100, loss=0.0458811
[INFO] evaluating...
             precision    recall  f1-score   support

          0       1.00      1.00      1.00       250
          1       1.00      1.00      1.00       250

avg / total       1.00      1.00      1.00       500


Traceback (most recent call last):
  File "E:\FENG\workspace_python\ch9_gradient_descent.py", line 92, in <module>
    plt.scatter(testX[:, 0], testX[:, 1], marker="o", c=testY, s=30)
  File "D:\ProgramFiles\Python27\lib\site-packages\matplotlib\pyplot.py", line 3470, in scatter
    edgecolors=edgecolors, data=data, **kwargs)
  File "D:\ProgramFiles\Python27\lib\site-packages\matplotlib\__init__.py", line 1855, in inner
    return func(ax, *args, **kwargs)
  File "D:\ProgramFiles\Python27\lib\site-packages\matplotlib\axes\_axes.py", line 4279, in scatter
    .format(c.shape, x.size, y.size))
ValueError: c of shape (500, 1) not acceptable as a color sequence for x with size 500, y with size 500

二、隨機梯度下降法（Stochastic Gradient Decent）

# import the necessary packages
from sklearn.model_selection import train_test_split
from sklearn.metrics import classification_report
from sklearn.datasets import make_blobs
import matplotlib.pyplot as plt
import numpy as np
import argparse

def sigmoid_activation(x):
	# compute the sigmoid activation value for a given input
	return 1.0 / (1 + np.exp(-x))
	
def predict(X, W):
	# take the dot product between our features and weight matrix
	preds = sigmoid_activation(X.dot(W))

	# apply a step function to threshold the outputs to binary
	# class labels
	preds[preds <= 0.5] = 0
	preds[preds > 0] = 1

	# return the predictions
	return preds
	
def next_batch(X, y, batchSize):
	# loop over our dataset ‘X‘ in mini-batches, yielding a tuple of
	# the current batched data and labels
	for i in np.arange(0, X.shape[0], batchSize):
		yield (X[i:i + batchSize], y[i:i + batchSize])

# construct the argument parse and parse the arguments
ap = argparse.ArgumentParser()
ap.add_argument("-e", "--epochs", type=float, default=100,
	help="# of epochs")
ap.add_argument("-a", "--alpha", type=float, default=0.01,
	help="learning rate")
ap.add_argument("-b", "--batch-size", type=int, default=32,
	help="size of SGD mini-batches")
args = vars(ap.parse_args())

# generate a 2-class classification problem with 1,000 data points,
# where each data point is a 2D feature vector
(X, y) = make_blobs(n_samples=1000, n_features=2, centers=2,
	cluster_std=1.5, random_state=1)
y = y.reshape((y.shape[0], 1))

# insert a column of 1’s as the last entry in the feature
# matrix -- this little trick allows us to treat the bias
# as a trainable parameter within the weight matrix
X = np.c_[X, np.ones((X.shape[0]))]

# partition the data into training and testing splits using 50% of
# the data for training and the remaining 50% for testing
(trainX, testX, trainY, testY) = train_test_split(X, y,
	test_size=0.5, random_state=42)
	
# initialize our weight matrix and list of losses
print("[INFO] training...")
W = np.random.randn(X.shape[1], 1)
losses = []

# loop over the desired number of epochs
for epoch in np.arange(0, args["epochs"]):
	# initialize the total loss for the epoch
	epochLoss = []

	# loop over our data in batches
	for (batchX, batchY) in next_batch(X, y, args["batch_size"]):
		# take the dot product between our current batch of features
		# and the weight matrix, then pass this value through our
		# activation function
		preds = sigmoid_activation(batchX.dot(W))

		# now that we have our predictions, we need to determine the
		# ‘error‘, which is the difference between our predictions
		# and the true values
		error = preds - batchY
		epochLoss.append(np.sum(error ** 2))
		
		# the gradient descent update is the dot product between our
		# current batch and the error on the batch
		gradient = batchX.T.dot(error)

		# in the update stage, all we need to do is "nudge" the
		# weight matrix in the negative direction of the gradient
		# (hence the term "gradient descent") by taking a small step
		# towards a set of "more optimal" parameters
		W += -args["alpha"] * gradient
		
	# update our loss history by taking the average loss across all
	# batches
	loss = np.average(epochLoss)
	losses.append(loss)

	# check to see if an update should be displayed
	if epoch == 0 or (epoch + 1) % 5 == 0:
		print("[INFO] epoch={}, loss={:.7f}".format(int(epoch + 1),
			loss))
			
# evaluate our model
print("[INFO] evaluating...")
preds = predict(testX, W)
print(classification_report(testY, preds))

# plot the (testing) classification data
plt.style.use("ggplot")
plt.figure()
plt.title("Data")
plt.scatter(testX[:, 0], testX[:, 1], marker="o", c=testY, s=30)

# construct a figure that plots the loss over time
plt.style.use("ggplot")
plt.figure()
plt.plot(np.arange(0, args["epochs"]), losses)
plt.title("Training Loss")
plt.xlabel("Epoch #")
plt.ylabel("Loss")
plt.show()

與第一種方法不同之處在於，每處理一小量資料，即按照該段資料更新權值矩陣。

執行結果如下：

================ RESTART: E:\FENG\workspace_python\ch9_sgd.py ================
[INFO] training...
[INFO] epoch=1, loss=0.5633928
[INFO] epoch=5, loss=0.0116136
[INFO] epoch=10, loss=0.0063118
[INFO] epoch=15, loss=0.0058116
[INFO] epoch=20, loss=0.0054206
[INFO] epoch=25, loss=0.0050830
[INFO] epoch=30, loss=0.0047875
[INFO] epoch=35, loss=0.0045260
[INFO] epoch=40, loss=0.0042924
[INFO] epoch=45, loss=0.0040821
[INFO] epoch=50, loss=0.0038914
[INFO] epoch=55, loss=0.0037176
[INFO] epoch=60, loss=0.0035583
[INFO] epoch=65, loss=0.0034118
[INFO] epoch=70, loss=0.0032764
[INFO] epoch=75, loss=0.0031509
[INFO] epoch=80, loss=0.0030342
[INFO] epoch=85, loss=0.0029253
[INFO] epoch=90, loss=0.0028235
[INFO] epoch=95, loss=0.0027281
[INFO] epoch=100, loss=0.0026385
[INFO] evaluating...
             precision    recall  f1-score   support

          0       1.00      1.00      1.00       250
          1       1.00      1.00      1.00       250

avg / total       1.00      1.00      1.00       500


Traceback (most recent call last):
  File "E:\FENG\workspace_python\ch9_sgd.py", line 109, in <module>
    plt.scatter(testX[:, 0], testX[:, 1], marker="o", c=testY, s=30)
  File "D:\ProgramFiles\Python27\lib\site-packages\matplotlib\pyplot.py", line 3470, in scatter
    edgecolors=edgecolors, data=data, **kwargs)
  File "D:\ProgramFiles\Python27\lib\site-packages\matplotlib\__init__.py", line 1855, in inner
    return func(ax, *args, **kwargs)
  File "D:\ProgramFiles\Python27\lib\site-packages\matplotlib\axes\_axes.py", line 4279, in scatter
    .format(c.shape, x.size, y.size))
ValueError: c of shape (500, 1) not acceptable as a color sequence for x with size 500, y with size 500

對比可見，SGD的損失下降比較快。