解梯度下降法的三種形式BGD、SGD以及MBGD
原帖地址:https://zhuanlan.zhihu.com/p/25765735
在應用機器學習算法時,我們通常采用梯度下降法來對采用的算法進行訓練。其實,常用的梯度下降法還具體包含有三種不同的形式,它們也各自有著不同的優缺點。
下面我們以線性回歸算法來對三種梯度下降法進行比較。
一般線性回歸函數的假設函數為:
$$h_\theta=\sum_{j=0}^n\theta_jx_j$$
對應的損失函數為:
$$J_{train}(\theta)=\frac1{2m}\sum_{i=1}^m(h_\theta(x^{(i)})-y^{(i))^2}$$
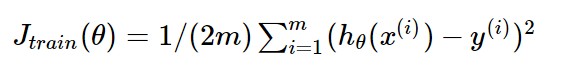
(這裏的1/2是為了後面求導計算方便)
下圖作為一個二維參數(,
)組對應能量函數的可視化圖:
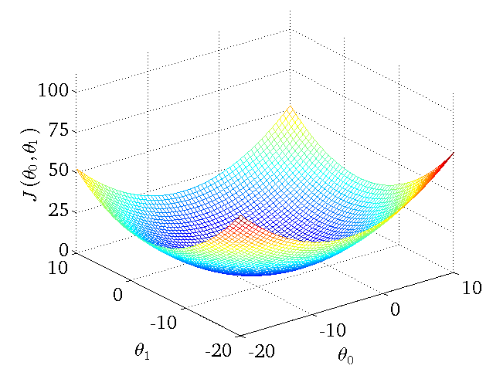
下面我們來分別講解三種梯度下降法
批量梯度下降法BGD
我們的目的是要誤差函數盡可能的小,即求解weights使誤差函數盡可能小。首先,我們隨機初始化weigths,然後不斷反復的更新weights使得誤差函數減小,直到滿足要求時停止。這裏更新算法我們選擇梯度下降算法,利用初始化的weights並且反復更新weights:
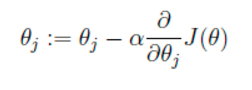 這裏
這裏代表學習率,表示每次向著J最陡峭的方向邁步的大小。為了更新weights,我們需要求出函數J的偏導數。首先當我們只有一個數據點(x,y)的時候,J的偏導數是:
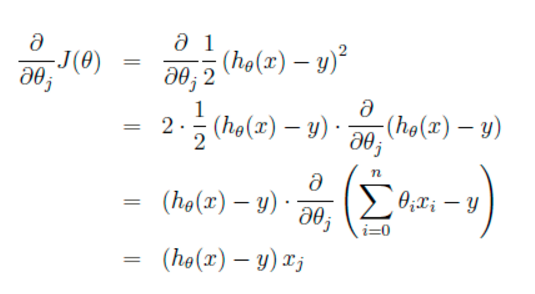
則對所有數據點,上述損失函數的偏導(累和)為:
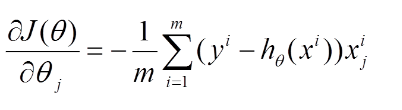 再最小化損失函數的過程中,需要不斷反復的更新weights使得誤差函數減小,更新過程如下:
再最小化損失函數的過程中,需要不斷反復的更新weights使得誤差函數減小,更新過程如下:
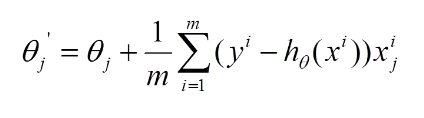 那麽好了,每次參數更新的偽代碼如下:
那麽好了,每次參數更新的偽代碼如下:
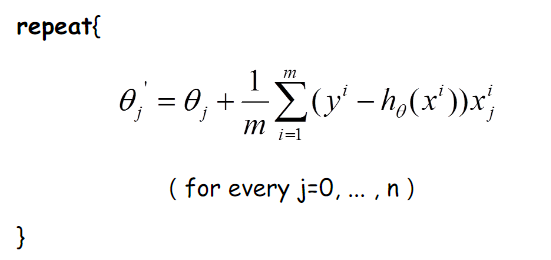
由上圖更新公式我們就可以看到,我們每一次的參數更新都用到了所有的訓練數據(比如有m個,就用到了m個),如果訓練數據非常多的話,是非常耗時的。
下面給出批梯度下降的收斂圖:
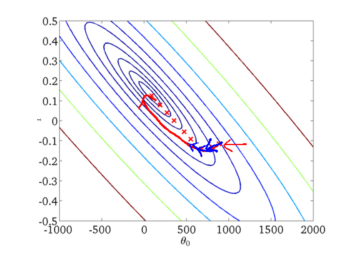
從圖中,我們可以得到BGD叠代的次數相對較少。
隨機梯度下降法SGD
由於批梯度下降每跟新一個參數的時候,要用到所有的樣本數,所以訓練速度會隨著樣本數量的增加而變得非常緩慢。隨機梯度下降正是為了解決這個辦法而提出的。它是利用每個樣本的損失函數對θ求偏導得到對應的梯度,來更新θ:
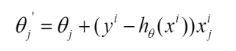
更新過程如下:
 隨機梯度下降是通過每個樣本來叠代更新一次,對比上面的批量梯度下降,叠代一次需要用到所有訓練樣本(往往如今真實問題訓練數據都是非常巨大),一次叠代不可能最優,如果叠代10次的話就需要遍歷訓練樣本10次。但是,SGD伴隨的一個問題是噪音較BGD要多,使得SGD並不是每次叠代都向著整體最優化方向。
隨機梯度下降是通過每個樣本來叠代更新一次,對比上面的批量梯度下降,叠代一次需要用到所有訓練樣本(往往如今真實問題訓練數據都是非常巨大),一次叠代不可能最優,如果叠代10次的話就需要遍歷訓練樣本10次。但是,SGD伴隨的一個問題是噪音較BGD要多,使得SGD並不是每次叠代都向著整體最優化方向。
隨機梯度下降收斂圖如下:
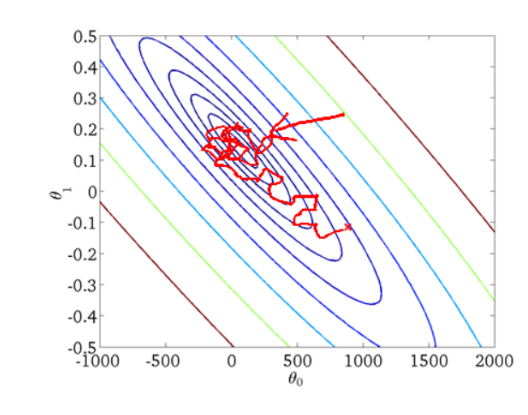
我們可以從圖中看出SGD叠代的次數較多,在解空間的搜索過程看起來很盲目。但是大體上是往著最優值方向移動。
min-batch 小批量梯度下降法MBGD
我們從上面兩種梯度下降法可以看出,其各自均有優缺點,那麽能不能在兩種方法的性能之間取得一個折衷呢?即,算法的訓練過程比較快,而且也要保證最終參數訓練的準確率,而這正是小批量梯度下降法(Mini-batch Gradient Descent,簡稱MBGD)的初衷。
我們假設每次更新參數的時候用到的樣本數為10個(不同的任務完全不同,這裏舉一個例子而已)
更新偽代碼如下:
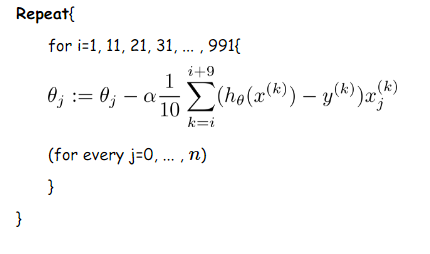
實例以及代碼詳解
這裏參考他人博客,創建了一個數據,如下圖所示:
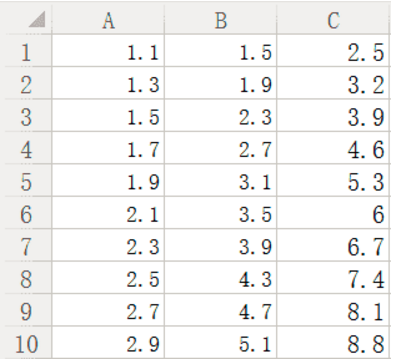 待訓練數據A、B為自變量,C為因變量。
待訓練數據A、B為自變量,C為因變量。
我希望通過這些訓練數據給我訓練出一個線性模型,用於進行下面數據的預測,test集合如下:
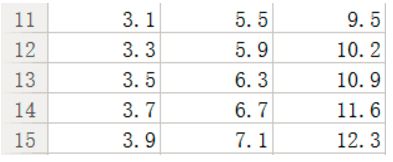
比如我們給出(3.1,5.5)希望模型預測出來的值與我們給定的9.5的差別是多少?這不是重點,重點是我們訓練模型過程中的參數更新方法(這是我們這篇文章的重點)批梯度下降以及隨機梯度下降代碼如何實現。下面分別來講:
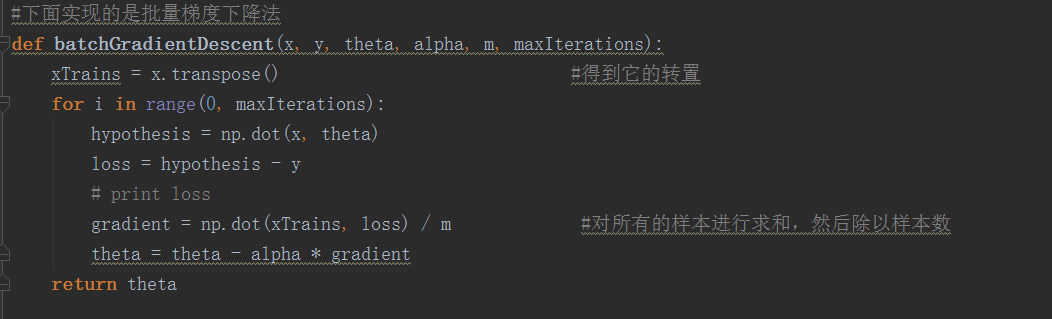
首先我們看批梯度下降法的代碼如下:
 這裏有可能還是比如抽象,為了讓大家更好的弄懂理解這倆個重要的方法,我下面結合例子,一行一行代碼解釋:
這裏有可能還是比如抽象,為了讓大家更好的弄懂理解這倆個重要的方法,我下面結合例子,一行一行代碼解釋:

我們看隨機梯度下降法的代碼如下:
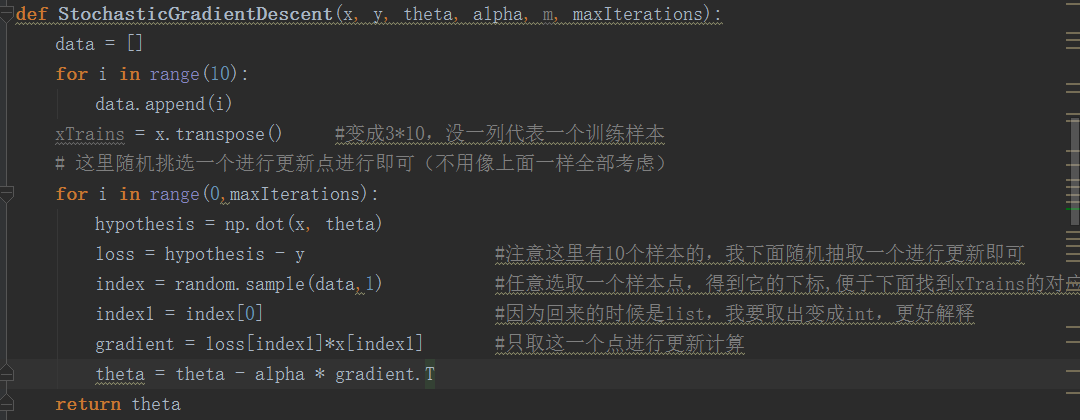
與批梯度下降最大的區別就在於,我們這裏更新參數的時候,並沒有將所有訓練樣本考慮進去,然後求和除以總數,而是我自己編程實現任取一個樣本點(代碼中random函數就能清楚看到),然後利用這個樣本點進行更新!這就是最大的區別!
那麽到這個時候,我們也非常容易知道小批量隨機梯度下降法的實現就是在這個的基礎上,隨機取batch個樣本,而不是1個樣本即可,掌握了本質就非常容易實現!
下面給出這個線性模型所有代碼,訓練,預測以及結果供參考:
#coding=utf-8
import numpy as np
import random
#下面實現的是批量梯度下降法
def batchGradientDescent(x, y, theta, alpha, m, maxIterations):
xTrains = x.transpose() #得到它的轉置
for i in range(0, maxIterations):
hypothesis = np.dot(x, theta)
loss = hypothesis - y
# print loss
gradient = np.dot(xTrains, loss) / m #對所有的樣本進行求和,然後除以樣本數
theta = theta - alpha * gradient
return theta
#下面實現的是隨機梯度下降法
def StochasticGradientDescent(x, y, theta, alpha, m, maxIterations):
data = []
for i in range(10):
data.append(i)
xTrains = x.transpose() #變成3*10,沒一列代表一個訓練樣本
# 這裏隨機挑選一個進行更新點進行即可(不用像上面一樣全部考慮)
for i in range(0,maxIterations):
hypothesis = np.dot(x, theta)
loss = hypothesis - y #註意這裏有10個樣本的,我下面隨機抽取一個進行更新即可
index = random.sample(data,1) #任意選取一個樣本點,得到它的下標,便於下面找到xTrains的對應列
index1 = index[0] #因為回來的時候是list,我要取出變成int,更好解釋
gradient = loss[index1]*x[index1] #只取這一個點進行更新計算
theta = theta - alpha * gradient.T
return theta
def predict(x, theta):
m, n = np.shape(x)
xTest = np.ones((m, n+1)) #在這個例子中,是第三列放1
xTest[:, :-1] = x #前倆列與x相同
res = np.dot(xTest, theta) #預測這個結果
return res
trainData = np.array([[1.1,1.5,1],[1.3,1.9,1],[1.5,2.3,1],[1.7,2.7,1],[1.9,3.1,1],[2.1,3.5,1],[2.3,3.9,1],[2.5,4.3,1],[2.7,4.7,1],[2.9,5.1,1]])
trainLabel = np.array([2.5,3.2,3.9,4.6,5.3,6,6.7,7.4,8.1,8.8])
m, n = np.shape(trainData)
theta = np.ones(n)
alpha = 0.1
maxIteration = 5000
#下面返回的theta就是學到的theta
theta = batchGradientDescent(trainData, trainLabel, theta, alpha, m, maxIteration)
print "theta = ",theta
x = np.array([[3.1, 5.5], [3.3, 5.9], [3.5, 6.3], [3.7, 6.7], [3.9, 7.1]])
print predict(x, theta)
theta = StochasticGradientDescent(trainData, trainLabel, theta, alpha, m, maxIteration)
print "theta = ",theta
x = np.array([[3.1, 5.5], [3.3, 5.9], [3.5, 6.3], [3.7, 6.7], [3.9, 7.1]])
print predict(x, theta)
#yes,is the code
最後運行結果為:
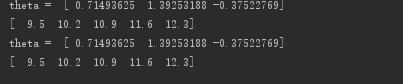 說明與我們給定的真實值是完全對應的。
說明與我們給定的真實值是完全對應的。
三種梯度下降方法的總結
1.批梯度下降每次更新使用了所有的訓練數據,最小化損失函數,如果只有一個極小值,那麽批梯度下降是考慮了訓練集所有數據,是朝著最小值叠代運動的,但是缺點是如果樣本值很大的話,更新速度會很慢。
2.隨機梯度下降在每次更新的時候,只考慮了一個樣本點,這樣會大大加快訓練數據,也恰好是批梯度下降的缺點,但是有可能由於訓練數據的噪聲點較多,那麽每一次利用噪聲點進行更新的過程中,就不一定是朝著極小值方向更新,但是由於更新多輪,整體方向還是大致朝著極小值方向更新,又提高了速度。
3.小批量梯度下降法是為了解決批梯度下降法的訓練速度慢,以及隨機梯度下降法的準確性綜合而來,但是這裏註意,不同問題的batch是不一樣的,聽師兄跟我說,我們nlp的parser訓練部分batch一般就設置為10000,那麽為什麽是10000呢,我覺得這就和每一個問題中神經網絡需要設置多少層,沒有一個人能夠準確答出,只能通過實驗結果來進行超參數的調整。
好了,本篇文章要講的已經講完了,真心希望對大家理解有幫助,歡迎大家指錯交流!
參考:
梯度下降算法以及其Python實現
[Machine Learning] 梯度下降法的三種形式BGD、SGD以及MBGD
解梯度下降法的三種形式BGD、SGD以及MBGD
