long long Euler(long long n)
{
    long long ans = n;
    for (long long i = 2; i * i <= n; i++)
    {
        if (n % i == 0)
        {
            ans = ans - ans / i;
            while (n % i == 0) n /= i;
        }
    }
    if (n > 1)
        ans = ans - ans / n;
    return ans;
}

利用遞推法求尤拉函式值：

演算法原理：開始令i的尤拉函式值等於它本身，如果i為偶數，可以利用定理二變為求奇數的。

若p是一個正整數滿足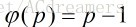，那麼p是素數，在遍歷過程中如果遇到尤拉函式值等於自身的情況，那麼

說明該數為素數。把這個數的尤拉函式值改變，同時也把能被該素因子整除的數改變。

void init()
{
    for (int i = 1; i < maxn; i++) Euler[i] = i;
    for (int i = 2; i < maxn; i += 2) Euler[i] >>= 1;
    for (int i = 3; i < maxn; i += 2)
    {
        if (Euler[i] == i)
        {
            for (int j = i; j < maxn; j += i)
                Euler[i] = Euler[i] - Euler[i] / i;
        }
    }
}