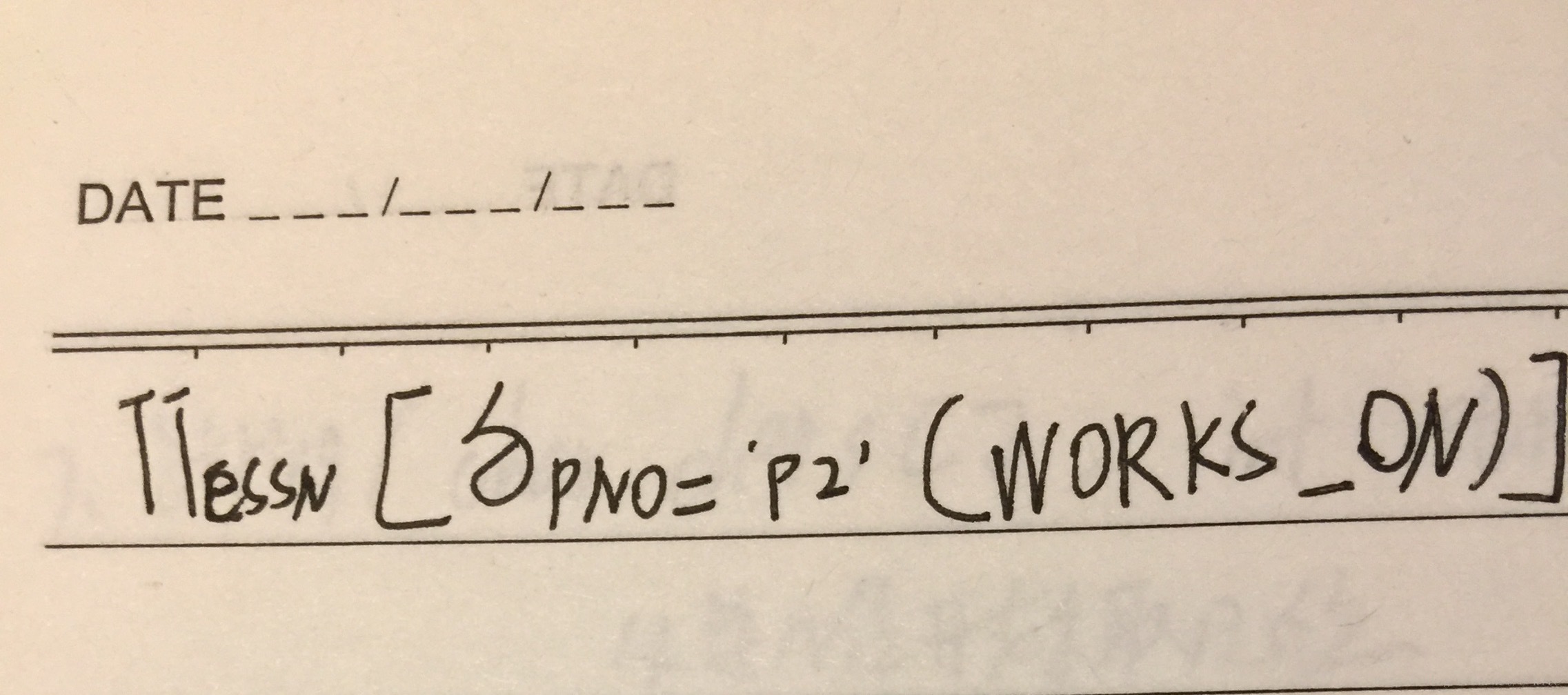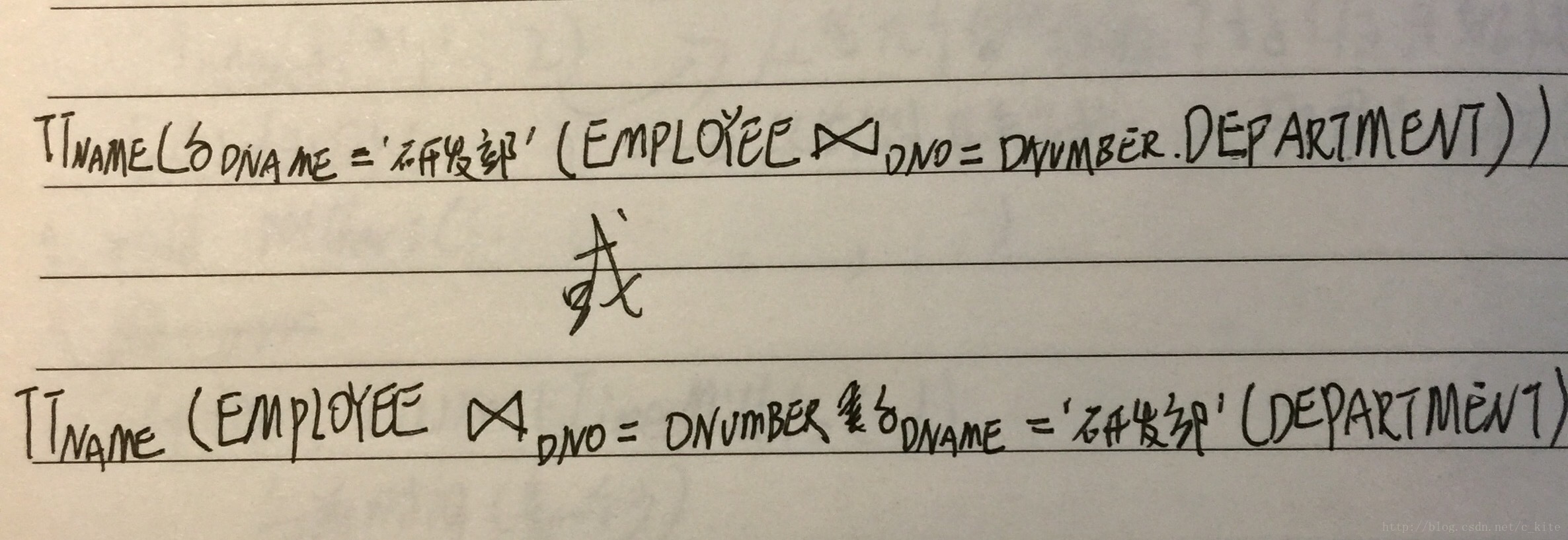關係資料庫

關係資料模型

關係是一個數學概念。
當把關係的概念引入到資料庫系統作為資料模型的資料結構時，既有所限定和也有所擴充。

關係的數學定義

例：

課程={離散,C語言…..}，學生={張三,李四…..}

笛卡兒積(cartesian product)：設D1、…、Dn是n個域。D1、…、Dn上的笛卡爾乘積定義為集合
D1×…×Dn ={ (d1 , …, dn ) | di ∈Di，1≤i≤n }。

解：

D1={離散,C語言…}，D2={張三,李四…}
D1×D2={(離散,張三),(離散,李四),……
       (C語言,張三),(C語言,李四),……
       …….}
 

關係(relation)：笛卡爾乘積D1×…×Dn的任意一個子集合稱為一個定義在域D1、…、Dn上的關係。

對數學定義的限定和擴充

限定：無限關係在資料庫系統中是無意義的。因此限定關係資料模型中的關係必須是有限集合。

數學上，(離散,張三)≠(張三,離散)
擴充：通過為關係的每個域附加一個屬性名的方法取消關係元組的有序性
資料庫上：(離散,張三)=(張三,離散)

基本關係具有以下六條性質：

• 列是同質的，即每一列中的分量是同一型別的資料；
• 不同的列可出自同一個域，稱其中的每一列為一個屬性，不同的屬性必須給不同的屬性名；
• 列的順序可任意交換；
• 任意兩個元組不能完全相同；
• 行的順序可任意交換；
• 分量必須取原子值，即每一個分量都必須是不可分的資料項。

完整性約束規則

幾個基本概念

• 候選鍵：給定關係模式R(U)，K屬於U，如果
  (1) R(U)的任何關係例項中的任意兩個元組在屬性集合K上的值都不相同－－－－唯一性
  (2) K的任何真子集都不滿足條件(1)－－－－極小性
  稱K是候選鍵。
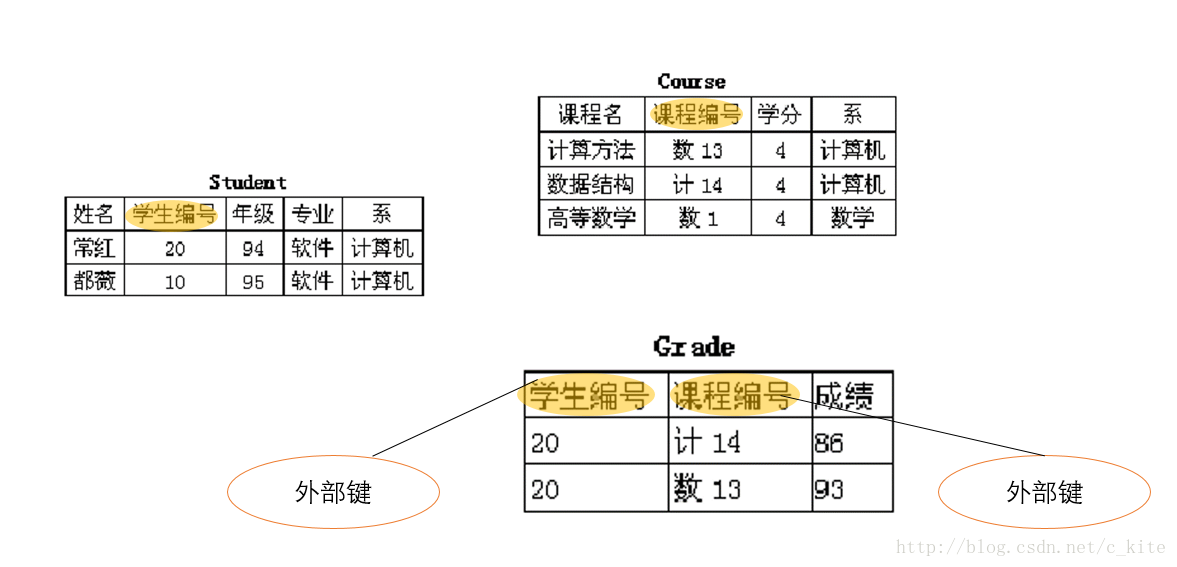
  例：Student(姓名, 學生編號, 年級, 專業, 系)
  顯然，學生編號是候選鍵。
  如果姓名不重複，姓名也是候選鍵。

• 主鍵：一個關係模式可能具有多個候選鍵。
  當一個關係中具有多個候選鍵時，我們選擇一個作為該關係模式的主鍵。
  候選鍵中的屬性稱為鍵(主)屬性，其他屬性稱為非鍵(主)屬性

• 外部鍵：設X是關係模式R(U)的一個屬性集合。如果X是另一個關係模式R’(U’)的主鍵，則稱X是R(U)關於R’(U’)的外部鍵。
  例：外部鍵
  

關聯完整性約束說明，任何關係的一個元組只能通過外部鍵與另一個關係中存在的元組相關聯.

關係運算

• 基於代數的定義：關係代數
  
• 基於邏輯的定義：關係演算
  由於使用變數的不同，關係演算又分為元組關係演算和域關係演算。

關係代數

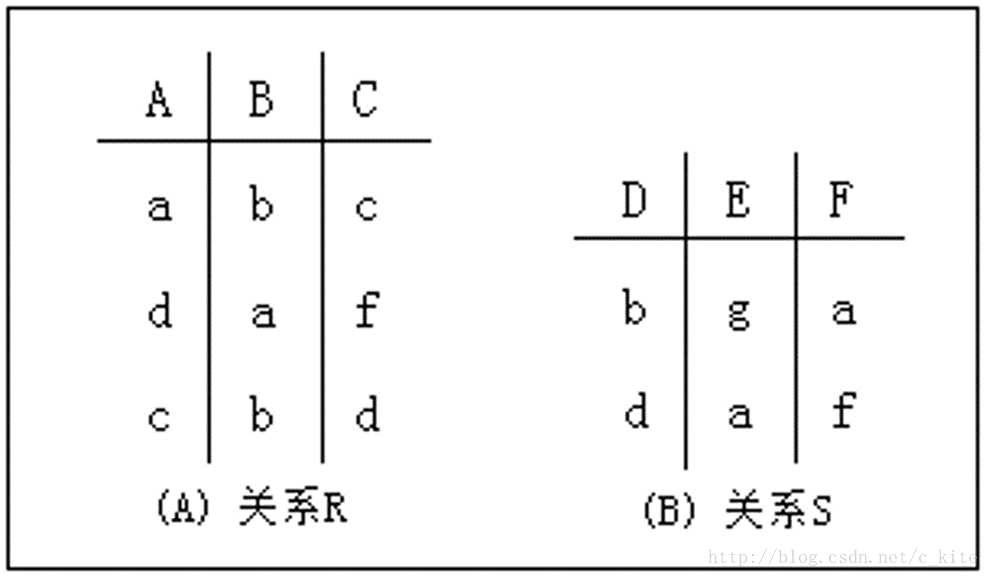
例: 兩個關係例項

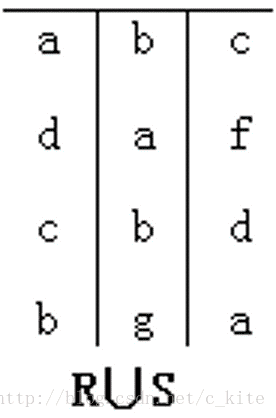
(1.) 並運算

設R和S是n元關係，而且兩者各對應屬性的資料型別也相同。R和S的並操作定義為 R∪S = { t | t∈R∨t∈S }。
白話: R和S關係合一起, 相同的不寫

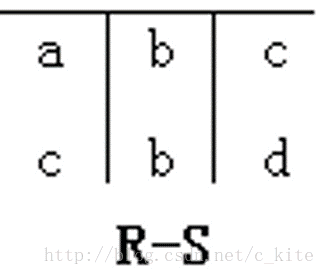
(2.) 差操作

設R和S是n元關係，而且兩者各對應屬性的資料型別也相同。R和S的差定義為 R-S ={ t | t∈R∧tS}。
白話: 因為是R-S, 找R在S關係中沒有的

(3.) 笛卡爾乘積

設R是n元關係，S是m元關係，R和S的的笛卡爾積定義為
R×S={(r1,…,rn,s1,…,sm)|(r1,…, rn )∈R∧(s1, …,sm )∈S}。
白話: 和普通的笛卡爾乘機差不多, 自己看看, 規律很好找.

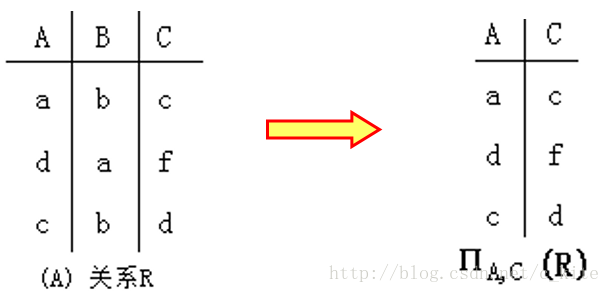
(4. ) 投影操作

設R是一個n元關係，R的投影操作定義為
∏i1,i2,…,im(R) = {(ri1, …,rim)|(r1 ,…,ri1,…,rim,…,rn)∈R}。
白話: 看橫行, 如果有兩個橫行相同, 只寫一個. 因此若是S關係投影操作的話, 也就是有b和a

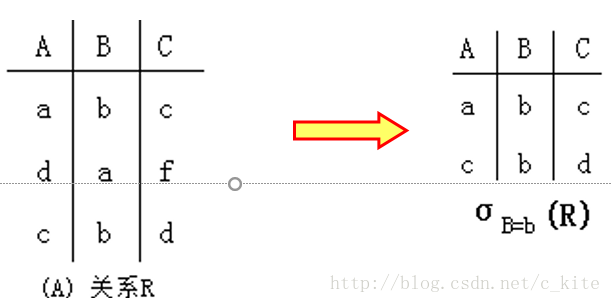
(5. ) 選擇操作

設R是一個n元關係，F是一個形如riθc的公式，其中θ∈{=，≠，>，<，≤，≥}，R的選擇操作定義為F(R)={(r1,…,ri ,…,rn )|(r1,…,ri ,…,rn )∈R∧riθc }。
白話: 把符合條件的拿出來

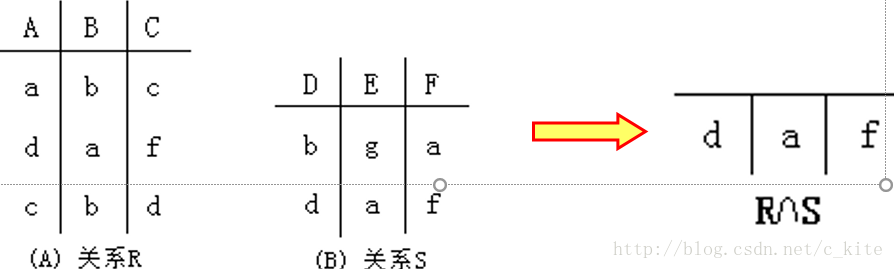
(6. ) 交操作

設R和S是n元關係，而且兩者各對應屬性的資料型別也相同。R和S的交操作定義為 R  S = { t | t∈R∧t∈S }= R-(R-S)。
白話: 相同的拿出來

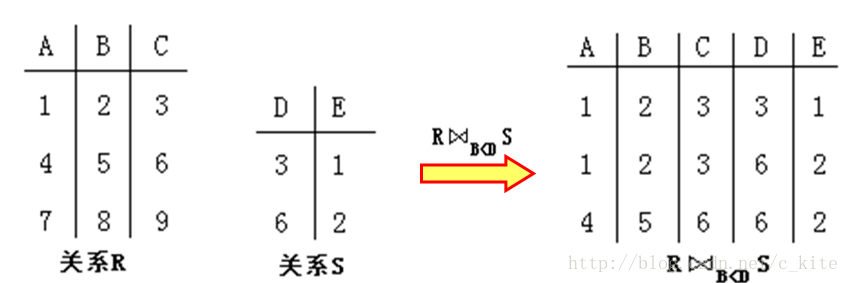
(7. ) 連線操作

設R是n元關係，S是m元關係，A是R的屬性，B是S的屬性，A和B的值域具有相同的資料型別，θ∈{=, ≠, >, <, ≤, ≥}。R和S的連線操作定義為

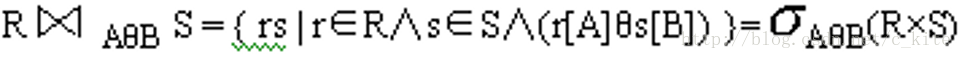
其中，r[A]表示元組r在屬性A上的值，s[B]表示元組s在屬性B上的值。我們稱A和B是連線屬性。

白話: 兩個關係先做笛卡爾積運算, 然後再根據條件進行比對. 留下符合條件的
例子:

(7. 1) 幾個特殊的連線操作

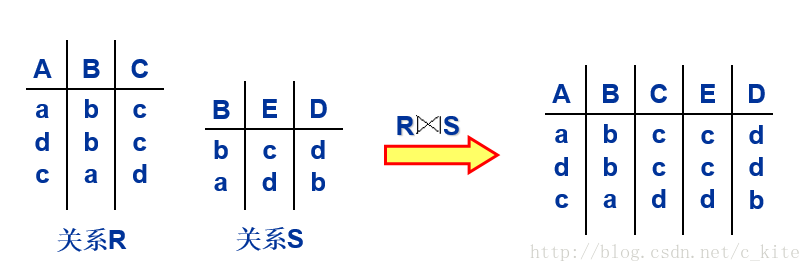
①自然連線 設Att(R)和Att(S)分別是R和S的屬性集合。連線條件為R.B=S.B，連線的結果關係的屬性集合為Att(R)∪(Att(S)-{B})，即B在結果關係中只出現一次。稱這樣的連線操作為自然連線操作，

白話: 找相同的然後拼在一起, 例如B屬性, 看看下面的例子;

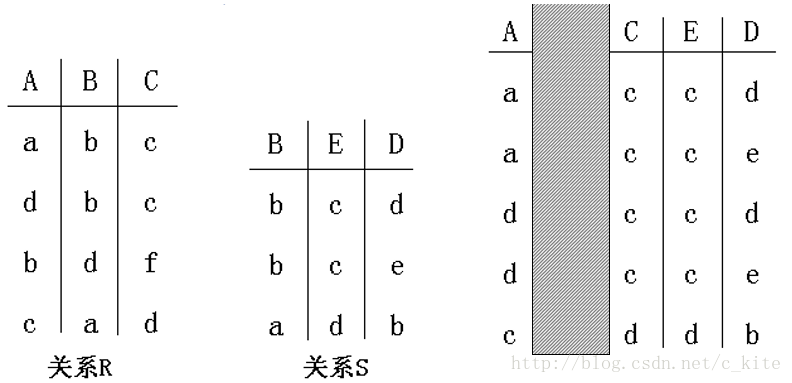
②複合連線 類似於自然連線，只是連線結果不包含連線屬性。

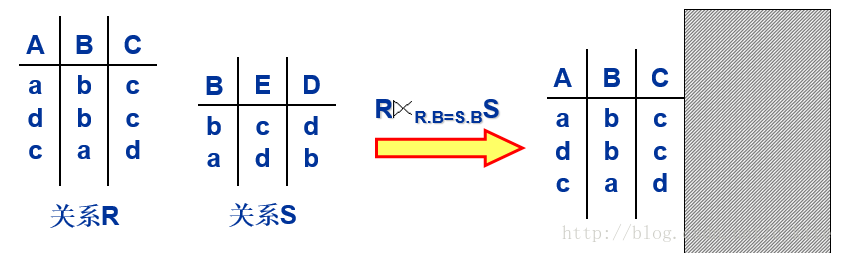
③半連線

白話: 下面的例子由於是R半連結S, 則因此拿R去和S所比較

(8. ) 商操作

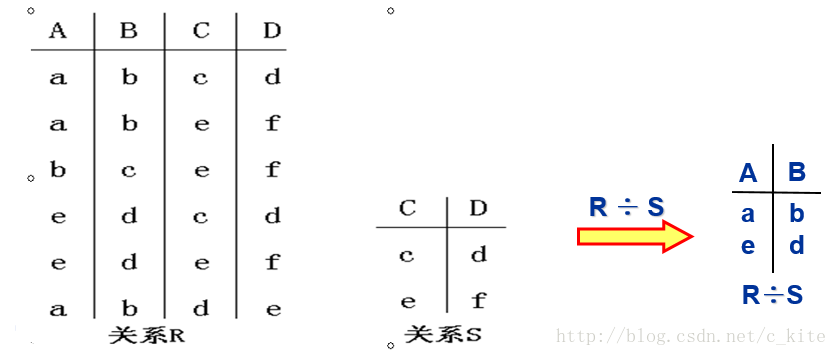
設R和S是兩個關係，Z是R的屬性集合，X是S的屬性集合，XZ，Y=Z-X。R除以S的商定義為R÷S={t|t∏Y(R)且sS, tsR}，其中，ts表示由t和s的各屬性值構成的一個R關係元組。

白話: 看下面的例子, 因為C, D是關係S中的兩個屬性, 因此在R集合對除了C, D的屬性, 即A, B兩屬性進行投影, 得到a, b; b, c; e, d;這三組, 然後用這個結果與關係S進行笛卡爾積運算, 發現b c c d這組在關係R中沒有, 其餘a, b; e, d; 做的運算在R中存在. 因此最後結果為a, b; e, d;

關係代數運算例題

一個COMPANY資料庫

下面介紹了一些需要用到的屬性解釋

NAME--員工名字
SSN--員工編號
SUPERSSN--上司編號
DNO--部門編號

DNUMBER--部門編號
MGRSSN--負責人編號

PNAME--專案名稱
PNUMBER--專案編號

ESSN--員工編號
PNO--專案編號

問1: 參加了p2專案的員工號(由於符號不太好打, 我手寫的)

語言解釋: 在WORKS_ON表中選擇PNO=P2的元組, 再對員工號即ESSN進行投影.

問2. 在“研發部”工作的所有工作人員名字

語言解釋: 1. EMPLOYEE表與DEPARTMENT表在部門編號相等的條件下, 進行連線, 然後再新表中選擇DNAME=”研發部”, 最後對NAME進行投影.
2 . 先在DEPARTMENT中選擇”研發部”, 然後與EMPLOYEE進行連線, 然後投影

問3. 沒有參加專案p1的工作人員名字

語言解釋: 在WORKS_ON中選擇P1專案, 與EMPLOYEE進行連線, 然後對NAME進行投影得到參加p1工作人員的名字, 最後用所有的名字減去它.