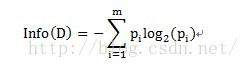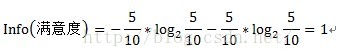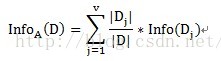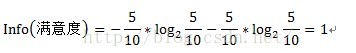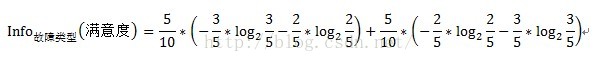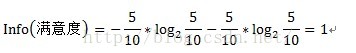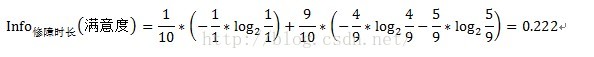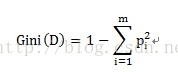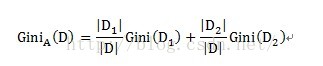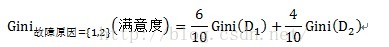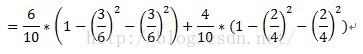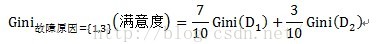決策樹ID3、C4.5、CART演算法:資訊熵,區別,剪枝理論總結
決策樹演算法:顧名思義,以二分類問題為例,即利用自變數構造一顆二叉樹,將目標變數區分出來,所有決策樹演算法的關鍵點如下:
1.分裂屬性的選擇。即選擇哪個自變數作為樹叉,也就是在n個自變數中,優先選擇哪個自變數進行分叉。而採用何種計算方式選擇樹叉,決定了決策樹演算法的型別,即ID3、c4.5、CART三種決策樹演算法選擇樹叉的方式是不一樣的,後文詳細描述。
2.樹剪枝。即在構建樹叉時,由於資料中的噪聲和離群點,許多分支反映的是訓練資料中的異常,而樹剪枝則是處理這種過分擬合的資料問題,常用的剪枝方法為先剪枝和後剪枝。後文詳細描述。
為了描述方便,本文采用評價電信服務保障中的滿意度預警專題來解釋決策樹演算法,即假如我家辦了電信的寬頻,有一天寬頻不能上網了,於是我打電話給電信報修,然後電信派相關人員進行維修,修好以後電信的回訪專員詢問我對這次修理障礙的過程是否滿意,我會給我對這次修理障礙給出相應評價,滿意或者不滿意。根據歷史資料可以建立滿意度預警模型,建模的目的就是為了預測哪些使用者會給出不滿意的評價。目標變數為二分類變數:滿意(記為0)和不滿意(記為1)。自變數為根據修理障礙過程產生的資料,如障礙型別、障礙原因、修障總時長、最近一個月發生故障的次數、最近一個月不滿意次數等等。簡單的資料如下:
客戶ID 故障原因 故障型別 修障時長 滿意度
001 1 5 10.2 1
002 1 5 12 0
003 1 5 14 1
004 2 5 16 0
005 2 5 18 1
006 2 6 20 0
007 3 6 22 1
008 3 6 23 0
009 3 6 24 1
010 3 6 25 0
故障原因和故障型別都為離散型變數,數字代表原因ID和型別ID。修障時長為連續型變數,單位為小時。滿意度中1為不滿意、0為滿意。
下面沿著分裂屬性的選擇和樹剪枝兩條主線,去描述三種決策樹演算法構造滿意度預警模型:
分裂屬性的選擇:即該選擇故障原因、故障型別、修障時長三個變數中的哪個作為決策樹的第一個分支。
ID3演算法是採用資訊增益來選擇樹叉,c4.5演算法採用增益率,CART演算法採用Gini指標。此外離散型變數和連續型變數在計算資訊增益、增益率、Gini指標時會有些區別。詳細描述如下:
1.ID3演算法的資訊增益:
資訊增益的思想來源於資訊理論的夏農定理,ID3演算法選擇具有最高資訊增益的自變數作為當前的樹叉(樹的分支),以滿意度預警模型為例,模型有三個自變數:故障原因、故障型別、修障時長。分別計算三個自變數的資訊增益,選取其中最大的資訊增益作為樹叉。資訊增益=原資訊需求-要按某個自變數劃分所需要的資訊。
如以自變數故障原因舉例,故障原因的資訊增益=原資訊需求(即僅僅基於滿意度類別比例的資訊需求,記為a)-按照故障原因劃分所需要的資訊需求(記為a1)。
其中原資訊需求a的計算方式為:
其中D為目標變數,此例中為滿意度。m=2,即滿意和不滿意兩種情況。Pi為滿意度中屬於分別屬於滿意和不滿意的概率。此例中共計10條資料,滿意5條,不滿意5條。概率都為1/2。Info(滿意度)即為僅僅基於滿意和滿意的類別比例進行劃分所需要的資訊需求,計算方式為:
按照故障原因劃分所需要的資訊需求(記為a1)可以表示為:
其中A表示目標變數D(即滿意度)中按自變數A劃分所需要的資訊,即按故障型別進行劃分所需要的資訊。V表示在目標變數D(即滿意度)中,按照自變數A(此處為故障原因)進行劃分,即故障原因分別為1、2、3進行劃分,將目標變數分別劃分為3個子集,{D1、D2、D3},因此V=3。即故障原因為1的劃分中,有2個不滿意和1個滿意。D1即指2個不滿意和1個滿意。故障原因為2的劃分中,有1個不滿意和2個滿意。D2即指1個不滿意和2個滿意。故障原因為3的劃分中,有2個不滿意和2個滿意。D3即指2個不滿意和2個滿意。具體公式如下:
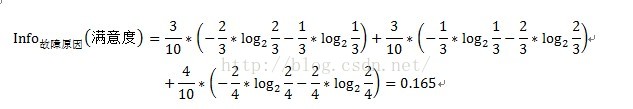
注:此處的計算結果即0.165不準確,沒有真正去算,結果僅供參考。
因此變數故障原因的資訊增益Gain(故障原因)=Info(滿意度)- Info故障原因(滿意度)=1-0.165=0.835
同樣的道理,變數故障型別的資訊增益計算方式如下:
變數故障型別的資訊增益Gain(故障型別)=1-0.205=0.795
故障原因和故障型別兩個變數都是離散型變數,按上述方式即可求得資訊增益,但修障時長為連續型變數,對於連續型變數該怎樣計算資訊增益呢?只需將連續型變數由小到大遞增排序,取相鄰兩個值的中點作為分裂點,然後按照離散型變數計算資訊增益的方法計算資訊增益,取其中最大的資訊增益作為最終的分裂點。如求修障時長的資訊增益,首先將修障時長遞增排序,即10.2、12、14、16、18、20、22、23、24、25,取相鄰兩個值的中點,如10.2和12,中點即為(10.2+12)/2=11.1,同理可得其他中點,分別為11.1、13、15、17、19、21、22.5、23.5、24.5。對每個中點都離散化成兩個子集,如中點11.1,可以離散化為兩個<=11.1和>11.1兩個子集,然後按照離散型變數的資訊增益計算方式計算其資訊增益,如中點11.1的資訊增益計算過程如下:
中點13的資訊增益計算過程如下:
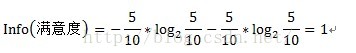
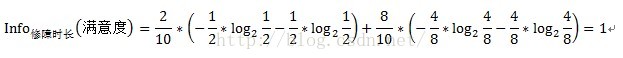
中點11.1的資訊增益Gain(修障時長)=1-1=0
同理分別求得各個中點的資訊增益,選取其中最大的資訊增益作為分裂點,如取中點11.1。然後與故障原因和故障型別的資訊增益相比較,取最大的資訊增益作為第一個樹叉的分支,此例中選取了故障原因作為第一個分叉。按照同樣的方式繼續構造樹的分支。
總之,資訊增益的直觀解釋為選取按某個自變數劃分所需要的期望資訊,該期望資訊越小,劃分的純度越高。因為對於某個分類問題而言,Info(D)都是固定的,而資訊增益Gain(A)=Info(D)-InfoA(D) 影響資訊增益的關鍵因素為:-InfoA(D),即按自變數A進行劃分,所需要的期望資訊越小,整體的資訊增益越大,越能將分類變數區分出來。
2.C4.5演算法的增益率:
由於資訊增益選擇分裂屬性的方式會傾向於選擇具有大量值的屬性(即自變數),如對於客戶ID,每個客戶ID對應一個滿意度,即按此變數劃分每個劃分都是純的(即完全的劃分,只有屬於一個類別),客戶ID的資訊增益為最大值1。但這種按該自變數的每個值進行分類的方式是沒有任何意義的。為了克服這一弊端,有人提出了採用增益率(GainRate)來選擇分裂屬性。計算方式如下:
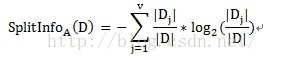
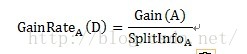
其中Gain(A)的計算方式與ID3演算法中的資訊增益計算方式相同。
以故障原因為例:
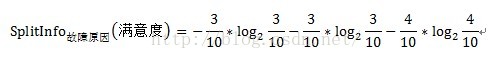
=1.201
Gain(故障原因)=0.835(前文已求得)
GainRate故障原因(滿意度)=1.201/0.835=1.438
同理可以求得其他自變數的增益率。
選取最大的資訊增益率作為分裂屬性。
3.CART演算法的Gini指標:
CART演算法選擇分裂屬性的方式是比較有意思的,首先計算不純度,然後利用不純度計算Gini指標。以滿意度預警模型為例,計算自變數故障原因的Gini指標時,先按照故障原因可能的子集進行劃分,即可以將故障原因具體劃分為如下的子集:{1,2,3}、{1,2}、{1,3}、{2,3}、{1}、{2}、{3}、{},共計8(2^V)個子集。由於{1,2,3}和{}對於分類來說沒有任何意義,因此實際分為2^V-2共計6個有效子集。然後計算這6個有效子集的不純度和Gini指標,選取最小的Gini指標作為分裂屬性。
不純度的計算方式為:
pi表示按某個變數劃分中,目標變數不同類別的概率。
某個自變數的Gini指標的計算方式如下:
對應到滿意度模型中,A為自變數,即故障原因、故障型別、修障時長。D代表滿意度,D1和D2分別為按變數A的子集所劃分出的兩個不同元組,如按子集{1,2}劃分,D1即為故障原因屬於{1,2}的滿意度評價,共有6條資料,D2即故障原因不屬於{1,2}的滿意度評價,共有3條資料。計運算元集{1,2}的不純度時,即Gini(D1),在故障原因屬於{1,2}的樣本資料中,分別有3條不滿意和3條滿意的資料,因此不純度為1-(3/6)^2-(3/6)^2=0.5。
以故障原因為例,計算過程如下:
計運算元集故障原因={1,3}的子集的Gini指標時,D1和D2分別為故障原因={1,3}的元組共計7條資料,故障原因不屬於{1,3}的元組即故障原因為2的資料,共計3條資料。詳細計算過程如下:
=0.52
樹的剪枝:
樹剪枝可以分為先剪枝和後剪枝。
先剪枝:通過提前停止樹的構造,如通過決定在給定的節點不再分裂或劃分訓練元組的子集,而對樹剪枝,一旦停止,該節點即成為樹葉。在構造樹時,可以使用諸如統計顯著性、資訊增益等度量評估分裂的優劣,如果劃分一個節點的元組低於預先定義閾值的分裂,則給定子集的進一步劃分將停止。但選取一個適當的閾值是困難的,較高的閾值可能導致過分簡化的樹,而較低的閾值可能使得樹的簡化太少。
後剪枝:它由完全生長的樹剪去子樹,通過刪除節點的分支,並用樹葉替換它而剪掉給定節點的子樹,樹葉用被替換的子樹中最頻繁的類標記。
其中c4.5使用悲觀剪枝方法,CART則為代價複雜度剪枝演算法(後剪枝)。
對比總結:
一、 C&R 樹
classification and regression trees 是一種基於樹的分類和預測方法,模型使用簡單,易於理解(規則解釋起來更簡明易),該方法通過在每個步驟最大限度降低不純潔度,使用遞迴分割槽來將訓練記錄分割為組。然後,可根據使用的建模方法在每個分割處自動選擇最合適的預測變數。如果節點中100% 的觀測值都屬於目標欄位的一個特定類別,則該節點將被認定為“純潔”。目標和預測變數欄位可以是範圍欄位,也可以是分類欄位;所有分割均為二元分割(即分割為兩組)。分割標準用的是基尼係數(Gini Index)。
CART即分類迴歸樹。如果目標變數是離散變數,則是classfication Tree,如果目標是連續變數,則是Regression Tree。
CART樹是二叉樹。 二叉樹有什麼優點?不像多叉樹那樣形成過多的資料碎片
二、C4.5離散化的過程
C4.5演算法是構造決策樹分類器的一種演算法。這種演算法利用比較各個描述性屬性的資訊增益值(Information Gain)的大小,來選擇Gain值最大的屬性進行分類。如果存在連續型的描述性屬性,那麼首先要把這些連續型屬性的值分成不同的區間,即“離散化”。把連續型屬性值“離散化”的方法是:
1.尋找該連續型屬性的最小值,並把它賦值給MIN,尋找該連續型屬性的最大值,並把它賦值給MAX;
2.設定區間【MIN,MAX】中的N個等分斷點Ai,它們分別是Ai=MIN+(MAX-MIN)/N*i,其中,i=1,2,……,N;
3.分別計算把【MIN,Ai】和(Ai,MAX】(i=1,2,……,N)作為區間值時的Gain值,並進行比較;
4.選取Gain值最大的Ak作為該連續型屬性的斷點,把屬性值設定為【MIN,Ak】和(Ak,MAX】兩個區間值。
CA.5演算法使用資訊增益的概念來構造決策樹,其中每個分類的決定都與所
擇的目標分類有關不確定性的最佳評估方法是平均資訊量,即資訊嫡(Entropy):
C4.5 決策樹
優點:執行效率和記憶體使用改進、適用大資料集
1) 面對資料遺漏和輸入欄位很多的問題時非常穩健;
2) 通常不需要很長的訓練次數進行估計;工作原理是基於產生最大資訊增益的欄位逐級分割樣本
3) 比一些其他型別的模型易於理解,模型推出的規則有非常直觀的解釋;
4) 允許進行多次多於兩個子組的分割。目標欄位必須為分類欄位
CART與ID3的區別
通過之前的研究發現,CART與ID3演算法都是基於資訊理論的決策樹演算法,CART演算法是一種通過計算Diversity(整體)-diversity(左節點)-diversity(右節點)的值取最佳分割的演算法。ID3和CART演算法的區別主要集中在樹的生成和樹的修剪方面,但是ID3演算法只能處理離散型的描述性屬性。C4.5演算法是ID3演算法的後續演算法,它能夠處理連續型資料。
CART中用於選擇變數的不純性度量是Gini指數;
如果目標變數是標稱的,並且是具有兩個以上的類別,則CART可能考慮將目標類別合併成兩個超類別(雙化);
如果目標變數是連續的,則CART演算法找出一組基於樹的迴歸方程來預測目標變數。
三、 QUEST決策樹
優點:運算過程比C&R 樹更簡單有效quick unbiased efficient statistical tree (快速無偏有效的統計樹)QUEST 節點可提供用於構建決策樹的二元分類法,此方法的設計目的是減少大型 C&R 決策樹分析所需的處理時間,同時減小分類樹方法中常見的偏向類別較多預測變數的趨勢。預測變數欄位可以是數字範圍的,但目標欄位必須是分類的。所有分割都是二元的。
四、CHAID決策樹
優點(chi-squared automatic interaction detection,卡方自動互動檢測),通過使用卡方統計量識別最優分割來構建決策樹的分類方法
1) 可產生多分支的決策樹
2) 目標和預測變數欄位可以是範圍欄位,也可以是分類欄位
3) 從統計顯著性角度確定分支變數和分割值,進而優化樹的分枝過程(前向修剪)
4) 建立在因果關係探討中,依據目標變數實現對輸入變數眾多水平劃分
五、樹的剪枝理論
1.樹的生長及變數處理
(1)對於離散變數X(x1…xn),分別取X變數各值的不同組合,將其分到樹的左枝或右枝,並對不同組合而產生的樹,進行評判,找出最佳組合。如變數年紀,其值有“少年”、“中年”、“老年”,則分別生產{少年,中年}和{老年},{上年、老年}和{中年},{中年,老年}和{少年},這三種組合,最後評判對目標區分最佳的組合。
(2)對於連續變數X(x1…xn),首先將值排序,分別取其兩相鄰值的平均值點作為分隔點,將樹一分成左枝和右枝,不斷掃描,進而判斷最佳分割點。
2. 變數和最佳切分點選擇原則
樹的生長,總的原則是,讓枝比樹更純,而度量原則是根據不純對指標來衡量,對於分類樹,則用GINI指標、Twoing指標、Order Twoing等;如果是迴歸樹則用,最小平方殘差、最小絕對殘差等指標衡量
(1)GINI指標(Gini越小,資料越純)——針對離散目標
(2)最小平方殘差——針對連續目標
其思想是,讓組內方差最小,對應組間方差最大,這樣兩組,也即樹分裂的左枝和右枝差異化最大。
(3)通過以上不純度指標,分別計算每個變數的各種切分/組合情況,找出該變數的最佳值組合/切分點;再比較各個變數的最佳值組合/切分點,最終找出最佳變數和該變數的最佳值組合/切分點
3. 目標值的估計
(1)分類樹:最終葉子中概率最大的類
(2)迴歸樹:最終葉子的均值或者中位數
4.樹的剪枝
(1)前剪枝( Pre-Pruning)
通過提前停止樹的構造來對決策樹進行剪枝,一旦停止該節點下樹的繼續構造,該節點就成了葉節點。一般樹的前剪枝原則有:
a.節點達到完全純度
b.樹的深度達到使用者所要的深度
c.節點中樣本個數少於使用者指定個數
d.不純度指標下降的最大幅度小於使用者指定的幅度
(2)後剪枝( Post-Pruning)
首先構造完整的決策樹,允許決策樹過度擬合訓練資料,然後對那些置信度不夠的結點的子樹用葉結點來替代。CART 採用Cost-Complexity Pruning(代價-複雜度剪枝法),代價(cost) :主要指樣本錯分率;複雜度(complexity) :主要指樹t的葉節點數,(Breiman…)定義樹t的代價複雜度(cost-complexity):
注:引數α:用於衡量代價與複雜度之間關係,表示剪枝後樹的複雜度降低程度與代價間的關係,如何定義α?
對t來說,剪掉它的子樹s,以t中最優葉節點代替,得到新樹new_t。 new_t可能會比t對於訓練資料分錯M個,但是new_t包含的葉節點數,卻比t少: (Leaf_s - 1)個。令替換之後代價複雜度相等:
5.CCP剪枝步驟:
第一步:
– 計算完全決策樹T_max的每個非葉節點的α值;
– 迴圈剪掉具有最小α值的子樹,直到剩下根節點
– 得到一系列剪枝(巢狀)樹{T_0,T_1,T_2,…T_m},其中T_0就是完全決策樹T_max。T_i+1是對T_i進行剪枝得到的結果
第二步:
– 使用獨立的剪枝集(非訓練集)對第一步中的T_i進行評估,獲取最佳剪枝樹
– 標準錯誤SE(standart error),公式:
– 最佳剪枝樹:T_best 是滿足以下條件並且包含的節點數最少的那顆剪枝樹。
參考文獻:
http://blog.sina.com.cn/s/blog_7399ad1f01014wec.html
http://blog.sina.com.cn/s/blog_4e4dec6c0101fdz6.html
http://blog.sina.com.cn/s/blog_5d6632e70101gh79.html