Savitzky-Golay濾波器（通常簡稱為S-G濾波器）最初由Savitzky和Golay於1964年提出，發表於Analytical Chemistry 雜誌。之後被廣泛地運用於資料流平滑除噪，是一種在時域內基於局域多項式最小二乘法擬合的濾波方法。這種濾波器最大的特點在於在濾除噪聲的同時可以確保訊號的形狀、寬度不變。

這種濾波方法其實是一種基於最小二乘擬合的濾波方法，這裡重點描述其推導過程並在最後給出其matlab程式實現。

訊號的最小二乘擬合

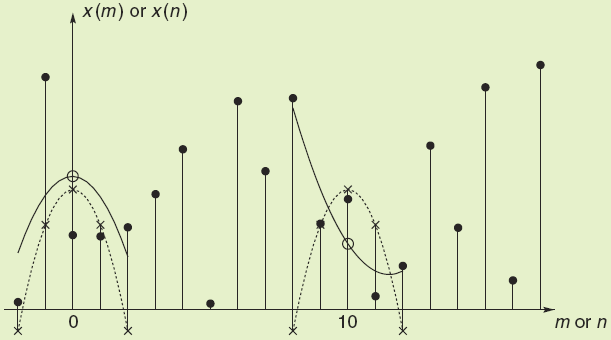
訊號的最小二乘擬合的基本思想可以用圖 1來說明

在平面座標系中，訊號可以看成一列離散的資料的集合，這列資料x[n]在圖1中用實心的圓點表示。可以用一條曲線來擬合這樣一組資料，不妨設這條曲線的方程為

當這組資料的每個點的橫座標帶入到曲線方程中可以得到其對應的函式值，而當其函式值與對應點的縱座標差值的平方和最小時，該曲線擬合度最高，從而可以由此求出方程係數。

現推導Savitzky-Golay濾波器的計算方法。考慮一組以為中心的2M+1個數據點，可用以下多項式p(n)來擬合它：

則其最小二乘擬合的殘差為：

使最小，令對係數求導，且導數為0，得：

即：

令：

則，原方程可以化簡為：

Savitzky-Golay使用簡單的多項式卷積方法，並制定了卷積係數表，通過卷積係數計算多項式係數，方便且快速。