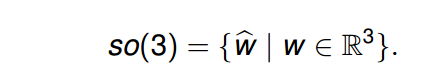SLAM筆記(九)再談李代數
內容接SLAM筆記(一)SLAM中的數學概覽
李群:
定義:實數空間上的連續群(對乘法、逆都是連續的,解析的)
舉例:如GL(n),SO(n),SE(n)
李代數(Lie algebra):
定義:由一個集合,一個數域,和一個二元運算[]組成;滿足封閉、雙線性、自反性、雅克比等價。
如3D中的叉乘:就屬於一個李代數。
李代數定義於李群的正切空間上,描述了李群中元素區域性性質。在剛體運動SE(3)中,李代數表徵某處的速度(在後邊會具體分析)
舉例:so(3),se(3)
1.李群求導
運算為李括號:
引入李代數的原因是:
對於旋轉矩陣R(t)(t指代角度),由於R(0) = I,所以旋轉矩陣可以一階近似表示:
若 = 0:
其中是一個關於向量 反對稱矩陣(skew-symmetric matrix)
它的推導如下::
這樣對旋轉矩陣R求導,只用直接左乘一個矩陣。如果R是單位矩陣,那它的導數就是,一個反對稱矩陣。
只有反對稱矩陣組成的空間,即 so(3),我們稱之為在單位矩陣處的正切空間tangent space。
為什麼這麼稱呼它?二維曲線在某處的導數是一條切線,三維曲線在某處的導數是一個切面,所以正切空間,實際上是導數所組成的空間。
對於一般非單位矩陣的旋轉矩陣R,只要求出了單位矩陣的的正切空間,然後在 右邊乘上這個矩陣R就可以求得R對應的正切空間了。
由於反映了R的導數性質,故稱它在SO(3)的正切空間(tangent space)上。
2.指數對映:
由於 , 該微分方程可以求得一般解為:
當R(0) = I 時,上式為:
這意味著可以通過指數對映,將so(3)(w)轉換為SO(3)(R)
代表如下所示的矩陣指數形式:
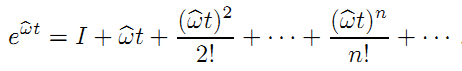
(3-1)
由於題主懶得修改截圖,此處將進行了歸一化,即我們在進行指數對映時,將原來的w’分解為,其中