圖論(二):圖的割點(cut vertex)與連通度(connectivity)
1. 割點與連通度
在無向連通圖中,刪除一個頂點v及其相連的邊後,原圖從一個連通分量變成了兩個或多個連通分量,則稱頂點v為割點,同時也稱關節點(Articulation Point)。一個沒有關節點的連通圖稱為重連通圖(biconnected graph)。若在連通圖上至少刪去k 個頂點才能破壞圖的連通性,則稱此圖的連通度為k。
關節點和重連通圖在實際中較多應用。顯然,一個表示通訊網路的圖的連通度越高,其系統越可靠,無論是哪一個站點出現故障或遭到外界破壞,都不影響系統的正常工作;又如,一個航空網若是重連通的,則當某條航線因天氣等某種原因關閉時,旅客仍可從別的航線繞道而行;再如,若將大規模的積體電路的關鍵線路設計成重連通的話,則在某些元件失效的情況下,整個片子的功能不受影響,反之,在戰爭中,若要摧毀敵方的運輸線,僅需破壞其運輸網中的關節點即可。
簡單的例子
(a)中G7 是連通圖,但不是重連通圖。圖中有三個關節點A、B 和G 。若刪去頂點B 以及所有依附頂點B 的邊,G7 就被分割成三個連通分量{A、C、F、L、M、J}、{G、H、I、K}和{D、E}。類似地,若刪去頂點A 或G 以及所依附於它們的邊,則G7 被分割成兩個連通分量。
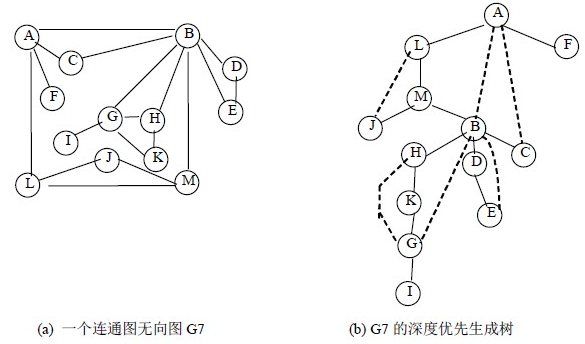
2. 求割點的方法
暴力的方法:
- 依次刪除每一個節點v
- 用DFS(或BFS)判斷還是否連通
- 再把節點v加入圖中
若用鄰接表(adjacency list),需要做VV次DFS,時間複雜度為O(V∗(V+E))O(V∗(V+E))。(題外話:我在面試實習的時候,只想到暴力方法;面試官提示只要一次DFS就就可以找到割點,當時死活都沒想出來)。
有關DFS搜尋樹的概念
在介紹演算法之前,先介紹幾個基本概念
- DFS搜尋樹:用DFS對圖進行遍歷時,按照遍歷次序的不同,我們可以得到一棵DFS搜尋樹,如圖(b)所示。
- 樹邊:(在[2]中稱為父子邊),在搜尋樹中的實線所示,可理解為在DFS過程中訪問未訪問節點時所經過的邊。
- 回邊:(在[2]中稱為返祖邊、後向邊),在搜尋樹中的虛線所示,可理解為在DFS過程中遇到已訪問節點時所經過的邊。
基於DFS的演算法
該演算法是R.Tarjan發明的。觀察DFS搜尋樹,我們可以發現有兩類節點可以成為割點:
- 對根節點u,若其有兩棵或兩棵以上的子樹,則該根結點u為割點;
- 對非葉子節點u(非根節點),若其子樹的節點均沒有指向u的祖先節點的回邊,說明刪除u之後,根結點與u的子樹的節點不再連通;則節點u為割點。
對於根結點,顯然很好處理;但是對於非葉子節點,怎麼去判斷有沒有回邊是一個值得深思的問題。
我們用dfn[u]記錄節點u在DFS過程中被遍歷到的次序號,low[u]記錄節點u或u的子樹通過非父子邊追溯到最早的祖先節點(即DFS次序號最小),那麼low[u]的計算過程如下:
下表給出圖(a)對應的dfn與low陣列值。
| i | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| vertex | A | B | C | D | E | F | G | H | I | J | K | L | M |
| dfn[i] | 1 | 5 | 12 | 10 | 11 | 13 | 8 | 6 | 9 | 4 | 7 | 2 | 3 |
| low[i] | 1 | 1 | 1 | 5 | 5 | 1 | 5 | 5 | 8 | 2 | 5 | 1 | 1 |
對於情況2,當(u,v)為樹邊且low[v] >= dfn[u]時,節點u才為割點。該式子的含義:以節點v為根的子樹所能追溯到最早的祖先節點要麼為v要麼為u。
程式碼實現
void dfs(int u) {
//記錄dfs遍歷次序
static int counter = 0;
//記錄節點u的子樹數
int children = 0;
ArcNode *p = graph[u].firstArc;
visit[u] = 1;
//初始化dfn與low
dfn[u] = low[u] = ++counter;
for(; p != NULL; p = p->next) {
int v = p->adjvex;
//節點v未被訪問,則(u,v)為樹邊
if(!visit[v]) {
children++;
parent[v] = u;
dfs(v);
low[u] = min(low[u], low[v]);
//case (1)
if(parent[u] == NIL && children > 1) {
printf("articulation point: %d\n", u);
}
//case (2)
if(parent[u] != NIL && low[v] >= dfn[u]) {
printf("articulation point: %d\n", u);
}
}
//節點v已訪問,則(u,v)為回邊
else if(v != parent[u]) {
low[u] = min(low[u], dfn[v]);
}
}
}採用鄰接表儲存圖,該演算法的時間複雜度應與DFS相同,為O(V+E)O(V+E)。
