§各種各樣的圖  

      

※簡單圖和多重圖

什麼是簡單圖？提到簡單圖就不得不提到他的對立面，也就是多重圖。

------------------------------------定義------------------------------------------------------

在無向圖中，關聯一對頂點的無向邊如果多於1條，則稱這些邊為平行邊，平行邊的條數稱為重數。在有向圖中，關聯一對頂點的有向邊如果多於1條，並且這些邊的始點與終點相同(也就是它們的的方向相同)，稱這些邊為平行邊。含平行邊的圖稱為

多重圖，既不含平行邊也不含環的圖稱為簡單圖。

---------------------------------------解釋-------------------------------------------------------

所謂簡單圖，對於無向圖而言就是：任取兩頂點，如果這兩個頂點之間的邊不超過一條就是簡單圖，否則為多重圖。

換言之====》假設這個無向圖是一張城市的地圖，那麼簡單圖就是這個城市極其不方便，想從A地到B地只有一條路可以走（但是所幸這條路不是單行道）。而多重圖大家就可以聯想一下北京或者上海四通八達的交通線路（這裡好像不太合適，畢竟交通線路也有單向的）。

而對於有向圖而言只有頂點相同且方向相同的才可以稱為多重圖（感覺還是可以照著無向圖理解，總之，簡單圖看起來無比不方便，無論是無向圖還是有向圖，有向圖尤為不便）。

下面放兩張圖片：

圖三

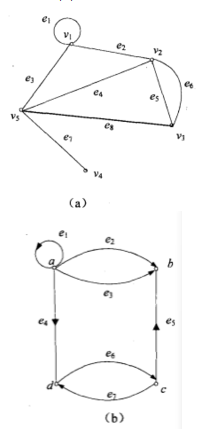
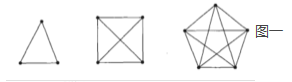
圖一就是簡單圖，圖二即為多重圖。

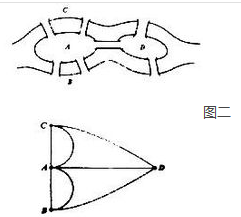
圖三也是多重圖，不過(a)是無向圖，(b)是有向圖

什麼是多重圖呢？

我們先看定義：

含有平行邊的圖稱為多重圖。也稱若圖中某兩個結點之間的邊數多於一條，又允許頂點通過同一條邊和自己關聯，則稱為多重圖。多重圖的定義和簡單圖是相對的。

最後小結一下（其實小結後面還要介紹別的）

上面介紹的是簡單圖和多重圖，他們是一對相對的概念，什麼叫相對的概念呢？舉個栗子：就像人的性別，如果我們定義了某種性別叫做女，那麼另一種性別肯定是男……

在無向圖中，關聯一對頂點的無向邊如果多於1條，則稱這些邊為平行邊，平行邊的條數稱為重數。在有向圖中，關聯一對頂點的有向邊如果多於1條，並且這些邊的始點與終點相同(也就是他們的方向相同)，稱這些邊為平行邊。含平行邊的圖稱為多重圖，既不含平行邊也不含環的圖稱為簡單圖。

※平凡圖和非平凡圖

平凡圖(Trivial graph)指僅有一個結點的圖，是離散數學與圖論的範疇。如果圖G是一個(1，0)圖，則稱為平凡圖，或者說是由一個孤立點組成的圖叫平凡圖。否則稱為非平凡圖。

在圖論中，有一個規定：至少有一個頂點才能稱為圖。===》這就說明：即使是最簡單的圖，至少也有一個頂點，那麼我們把這種看起來很不像圖的圖（只有一個頂點，反正看起來很隨意了，但是至少比什麼都沒有好）。

同時，注意：

這同時說明，在圖論中是沒有∅的，大家不要想了。

具體有什麼用以後用到了會回來補充的。

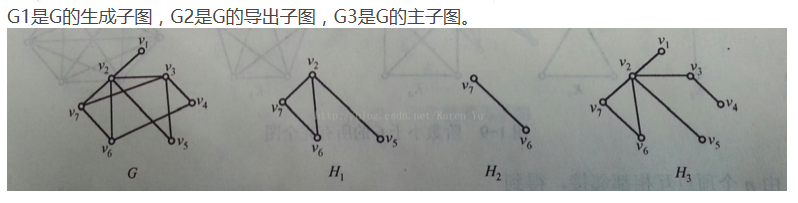
※母圖和子圖（+補圖） 要想理解生成子圖和匯出子圖，首先得了解一個概念——母圖是什麼？（就像洋務運動的時候容閎跟曾國藩說，要想自己造機器，首先得有一個母機）

子圖

什麼是子圖呢？

首先，大家在高中學集合的時候肯定接觸過子集，真子集和非空真子集（我記得高中老師特別喜歡在判斷是否可以是空集這裡挖坑），回憶一下子集，那麼就大概能理解子圖的概念了。

子圖的定義

設 為兩個圖（同為 無向圖或同為 有向圖），若 且 ，則稱G'是G的 子圖，G是G‘的 母圖，記作 ，又若 且 ，則G'稱是G的 真子圖，若 ，則稱G'是G的 生成子圖。 設 為一圖， 且 ,稱以 為頂點集，以G中兩個端點都在 中的邊組成邊集 的圖為G的 匯出子圖，記作 ，又設 且 ，稱以 為邊集，以 中邊關聯的頂點為頂點集 的圖為G的 匯出的子圖，記作 。 在圖1中，設G如圖1(a)所示，取 ，則 的匯出子圖 如圖1(b)所示，取 ，則 的匯出子圖 如圖1(c)所示。

圖G＝[E,V]（E為“邊”集.V為“頂點”集）,G′＝[E′,V′],
如果：E′≤E.（≤：借用符號,意思是包含於）,V′≤V,
則G′叫G的子圖.
如果：E′≤E,而V′＝V.（!）,
則G′叫G的生成子圖.
區別就是生成子圖的頂點,與原圖完全一樣,而子圖確可以少一些.
生成子圖的英譯是：spanning subgraph.
induced subgraph的漢譯是“誘導子圖”,或者“匯出子圖”.兩者不同.
而後者的意思是：G′＝[E′,V′].
V′≤V,（可以少,也可以不少）.對於V′的所有頂點,只要在G中有連邊,這個邊就在G′出現.也說G′是G的由V′誘匯出的子圖.記為G′＝G[V′].

匯出子圖

假設V’是V（G）的一個非空子集，以V'為頂點集，以兩端點均在V'中的邊的全體為邊集所組成G的子圖，稱為G的由V'匯出的子圖（Induced Subgraph），記為G[V']。圖中H1是由{v2,v5,v6,v7}匯出的子圖，即H1=G[{v2,v5,v6,v7}]。

匯出子圖G[V-V']記為G-V'，它是從G中刪除V'中的頂點以及與這些頂點相關聯的邊所得到的子圖。

若V'={v}，長把G-{v}簡記為G-v。

補圖 設 為n階無向簡單圖，以V為頂點集，以所有使G成為完全圖的 的新增邊組成的集合為邊集的圖，稱為G的 補圖，記作 。 若圖 ，則稱G是自補圖。 圖2中，（b）和（c）互為補圖，（a）是自補圖。
定理（來自百度百科）： 若n階圖G是自補圖，則 或 ，k為非負整數，且圖G有 條邊。 證明：因為n階圖G是自補圖，所以G與 同構。於是完全圖 的 條邊將各有一半為G與 的邊，即G與 均有 條邊。而圖G的邊數是非負整數，故4一定能整除 ，而連續的兩個整數n-1與n總是一個為奇數，一個為偶數，故 或 （k為非負整數）。證畢。
※完全圖 在圖論的數學領域，完全圖是一個簡單的無向圖，其中每對不同的頂點之間都恰連有一條邊相連。完整的有向圖又是一個有向圖，其中每對不同的頂點通過一對唯一的邊緣（每個方向一個）連線。n個端點的完全圖有n個端點以及n(n − 1) / 2條邊，以Kn表示。它是(k − 1)-正則圖。所有完全圖都是它本身的團（clique）。 按照定義，我們可以類比一下簡單圖，可以這麼說，完全圖一定是簡單圖，因為完全圖符合簡單圖的定義，即每兩個頂點之間只有一條邊，那麼我們可不可以說簡單圖一定是多重圖呢？顯然不能，退一步說，如果二者等價，那麼在這麼漫長的歲月裡，“懶惰的”數學家肯定只會保留一個名字，而不會留下兩個概念。現在提出反例就很好理解了，我們假設現在有一個完全圖，這個完全圖有A B兩個頂點，A B兩個頂點之間有一條邊，此時當然這還是一個完全圖，同時也是簡單圖，但是，如果我們增加一個頂點C，將頂點C與頂點A相連，而不連線BC，此時，這張圖就不是完全圖了，但她還是簡單圖。
n個頂點的完全圖表示為 。 一些訊息來源稱，這個符號中的字母K代表德語單詞komplett，但完全圖的德文名稱vollständigerGraph不包含字母K，其他來源則表示符號表示 Kazimierz Kuratowski圖論。 具有 個邊（三角數），並且是維度為n-1的常規圖。所有完全圖都是它們自己的最大組。 它們是最大化連線的，因為斷開圖形的唯一頂點是所有的頂點集。完全圖的補碼圖是一個空圖。
無向完全圖： 無向完全圖是用n表示圖中頂點數目的一種圖，一張圖中每條邊都是無方向的。 ^[2]   ---定義--- 用n表示圖中頂點數目，用e表示邊或弧的數目。若<vi,vj>∈VR，則vi≠vj，那麼，對於 無向圖，e的取值範圍是0到，有條邊的無向圖稱為 完全圖。 ---解釋--- 直觀來說，若一個圖中每條邊都是無方向的，則稱為 無向圖。 （1）無向邊的表示 無向圖中的邊均是頂點的無序對，無序對通常用圓括號表示。 【例】無序對(vi，vj)和(vj，vi)表示同一條邊。 （2）無向圖的表示 【例】下面(b)圖中的G2和(c)圖中的G3均是無向圖，它們的頂點集和邊集分別為： V(G2)={v1，v2，v3，v4} E(G2)={(vl，v2)，(v1，v3)，(v1，v4)，(v2，v3)，(v2，v4)，(v3，v4)} V(G3)={v1，v2，v3，v4，v5，v6，v7} E(G3)={(v1，v2)，(vl，v3)，(v2，v4)，(v2，v5)，(v3，v6)，(v3，v7)}
---注意--- 在以下討論中，不考慮頂點到其自身的邊。即若(v1，v2)或<vl，v2>是E(G)中的一條邊，則要求v1≠v2。此外，不允許一條邊在圖中重複出現，即只討論簡單的圖。 3．圖G的頂點數n和邊數e的關係 （1）若G是 無向圖，則0≤e≤n(n-1)/2 恰有n(n-1)/2條邊的無向圖稱無向完全圖(Undirected Complete Graph) （2）若G是 有向圖，則0≤e≤n(n-1)。 恰有n(n-1)條邊的有向圖稱為 有向完全圖(Directed Complete Graph)。 注意： 完全圖具有最多的邊數。任意一對頂點間均有邊相連。
有向完全圖： 用n表示圖中頂點數目，用e表示邊或弧的數目。若<vi,vj>∈VR，則 ≠ ，那麼，對於有向圖，e的 取值範圍是0到 ，有 條邊的有向圖稱為有向完全圖。

※空圖

根據圖論中圖的定義：G=<V(G),E(G)>(V(G)是節點的有窮非空集合，E(G)是邊集合)，則V(G)不能為空，空圖是錯誤地將V(G)為空集作為一種情況列了出來（則E(G)也為空集），稱為空圖。

※正則圖

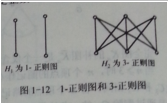
正則圖是指各頂點的度均相同的無向簡單圖。 在圖論中，正則圖中每個頂點具有相同數量的鄰點； 即每個頂點具有相同的 度或 價態。 正則的 有向圖也必須滿足更多的條件，即每個頂點的內外自由度都要彼此相等。具有k個自由度的頂點的正則圖被稱為k度的k-正則圖。 此外，奇數程度的正則圖形將包含偶數個頂點。
如果一個圖中的每個頂點的度是某一固定整數k，則稱該圖是k-正則圖（k-regular）。正則圖中δ（G）=Δ（G）。圖1-12所示為1-正則圖和3-正則圖。 如圖：

§各種各樣的圖  

      

※簡單圖和多重圖

什麼是簡單圖？提到簡單圖就不得不提到他的對立面，也就是多重圖。

------------------------------------定義------------------------------------------------------

在無向圖中，關聯一對頂點的無向邊如果多於1條，則稱這些邊為平行邊，平行邊的條數稱為重數。在有向圖中，關聯一對頂點的有向邊如果多於1條，並且這些邊的始點與終點相同(也就是它們的的方向相同)，稱這些邊為平行邊。含平行邊的圖稱為多重圖，既不含平行邊也不含環的圖稱為簡單圖。

---------------------------------------解釋-------------------------------------------------------

所謂簡單圖，對於無向圖而言就是：任取兩頂點，如果這兩個頂點之間的邊不超過一條就是簡單圖，否則為多重圖。

換言之====》假設這個無向圖是一張城市的地圖，那麼簡單圖就是這個城市極其不方便，想從A地到B地只有一條路可以走（但是所幸這條路不是單行道）。而多重圖大家就可以聯想一下北京或者上海四通八達的交通線路（這裡好像不太合適，畢竟交通線路也有單向的）。

而對於有向圖而言只有頂點相同且方向相同的才可以稱為多重圖（感覺還是可以照著無向圖理解，總之，簡單圖看起來無比不方便，無論是無向圖還是有向圖，有向圖尤為不便）。

下面放兩張圖片：

圖三

圖一就是簡單圖，圖二即為多重圖。

圖三也是多重圖，不過(a)是無向圖，(b)是有向圖

什麼是多重圖呢？

我們先看定義：

含有平行邊的圖稱為多重圖。也稱若圖中某兩個結點之間的邊數多於一條，又允許頂點通過同一條邊和自己關聯，則稱為多重圖。多重圖的定義和簡單圖是相對的。

最後小結一下（其實小結後面還要介紹別的）

上面介紹的是簡單圖和多重圖，他們是一對相對的概念，什麼叫相對的概念呢？舉個栗子：就像人的性別，如果我們定義了某種性別叫做女，那麼另一種性別肯定是男……

在無向圖中，關聯一對頂點的無向邊如果多於1條，則稱這些邊為平行邊，平行邊的條數稱為重數。在有向圖中，關聯一對頂點的有向邊如果多於1條，並且這些邊的始點與終點相同(也就是他們的方向相同)，稱這些邊為平行邊。含平行邊的圖稱為多重圖，既不含平行邊也不含環的圖稱為簡單圖。

※平凡圖和非平凡圖

平凡圖(Trivial graph)指僅有一個結點的圖，是離散數學與圖論的範疇。如果圖G是一個(1，0)圖，則稱為平凡圖，或者說是由一個孤立點組成的圖叫平凡圖。否則稱為非平凡圖。

在圖論中，有一個規定：至少有一個頂點才能稱為圖。===》這就說明：即使是最簡單的圖，至少也有一個頂點，那麼我們把這種看起來很不像圖的圖（只有一個頂點，反正看起來很隨意了，但是至少比什麼都沒有好）。

同時，注意：

這同時說明，在圖論中是沒有∅的，大家不要想了。

具體有什麼用以後用到了會回來補充的。

※母圖和子圖（+補圖） 要想理解生成子圖和匯出子圖，首先得了解一個概念——母圖是什麼？（就像洋務運動的時候容閎跟曾國藩說，要想自己造機器，首先得有一個母機）

子圖

什麼是子圖呢？

首先，大家在高中學集合的時候肯定接觸過子集，真子集和非空真子集（我記得高中老師特別喜歡在判斷是否可以是空集這裡挖坑），回憶一下子集，那麼就大概能理解子圖的概念了。

子圖的定義

設 為兩個圖（同為 無向圖或同為 有向圖），若 且 ，則稱G'是G的 子圖，G是G‘的 母圖，記作 ，又若 且 ，則G'稱是G的 真子圖，若 ，則稱G'是G的 生成子圖。 設 為一圖， 且 ,稱以 為頂點集，以G中兩個端點都在 中的邊組成邊集 的圖為G的 匯出子圖，記作 ，又設 且 ，稱以 為邊集，以 中邊關聯的頂點為頂點集 的圖為G的 匯出的子圖，記作 。 在圖1中，設G如圖1(a)所示，取 ，則 的匯出子圖 如圖1(b)所示，取 ，則 的匯出子圖 如圖1(c)所示。

圖G＝[E,V]（E為“邊”集.V為“頂點”集）,G′＝[E′,V′],
如果：E′≤E.（≤：借用符號,意思是包含於）,V′≤V,
則G′叫G的子圖.
如果：E′≤E,而V′＝V.（!）,
則G′叫G的生成子圖.
區別就是生成子圖的頂點,與原圖完全一樣,而子圖確可以少一些.
生成子圖的英譯是：spanning subgraph.
induced subgraph的漢譯是“誘導子圖”,或者“匯出子圖”.兩者不同.
而後者的意思是：G′＝[E′,V′].
V′≤V,（可以少,也可以不少）.對於V′的所有頂點,只要在G中有連邊,這個邊就在G′出現.也說G′是G的由V′誘匯出的子圖.記為G′＝G[V′].

匯出子圖

假設V’是V（G）的一個非空子集，以V'為頂點集，以兩端點均在V'中的邊的全體為邊集所組成G的子圖，稱為G的由V'匯出的子圖（Induced Subgraph），記為G[V']。圖中H1是由{v2,v5,v6,v7}匯出的子圖，即H1=G[{v2,v5,v6,v7}]。

匯出子圖G[V-V']記為G-V'，它是從G中刪除V'中的頂點以及與這些頂點相關聯的邊所得到的子圖。

若V'={v}，長把G-{v}簡記為G-v。

補圖 設 為n階無向簡單圖，以V為頂點集，以所有使G成為完全圖的 的新增邊組成的集合為邊集的圖，稱為G的 補圖，記作 。 若圖 ，則稱G是自補圖。 圖2中，（b）和（c）互為補圖，（a）是自補圖。
定理（來自百度百科）： 若n階圖G是自補圖，則 或 ，k為非負整數，且圖G有 條邊。 證明：因為n階圖G是自補圖，所以G與 同構。於是完全圖 的 條邊將各有一半為G與 的邊，即G與 均有 條邊。而圖G的邊數是非負整數，故4一定能整除 ，而連續的兩個整數n-1與n總是一個為奇數，一個為偶數，故 或 （k為非負整數）。證畢。
※完全圖 在圖論的數學領域，完全圖是一個簡單的無向圖，其中每對不同的頂點之間都恰連有一條邊相連。完整的有向圖又是一個有向圖，其中每對不同的頂點通過一對唯一的邊緣（每個方向一個）連線。n個端點的完全圖有n個端點以及n(n − 1) / 2條邊，以Kn表示。它是(k − 1)-正則圖。所有完全圖都是它本身的團（clique）。 按照定義，我們可以類比一下簡單圖，可以這麼說，完全圖一定是簡單圖，因為完全圖符合簡單圖的定義，即每兩個頂點之間只有一條邊，那麼我們可不可以說簡單圖一定是多重圖呢？顯然不能，退一步說，如果二者等價，那麼在這麼漫長的歲月裡，“懶惰的”數學家肯定只會保留一個名字，而不會留下兩個概念。現在提出反例就很好理解了，我們假設現在有一個完全圖，這個完全圖有A B兩個頂點，A B兩個頂點之間有一條邊，此時當然這還是一個完全圖，同時也是簡單圖，但是，如果我們增加一個頂點C，將頂點C與頂點A相連，而不連線BC，此時，這張圖就不是完全圖了，但她還是簡單圖。
n個頂點的完全圖表示為 。 一些訊息來源稱，這個符號中的字母K代表德語單詞komplett，但完全圖的德文名稱vollständigerGraph不包含字母K，其他來源則表示符號表示 Kazimierz Kuratowski圖論。 具有 個邊（三角數），並且是維度為n-1的常規圖。所有完全圖都是它們自己的最大組。 它們是最大化連線的，因為斷開圖形的唯一頂點是所有的頂點集。完全圖的補碼圖是一個空圖。
無向完全圖： 無向完全圖是用n表示圖中頂點數目的一種圖，一張圖中每條邊都是無方向的。 ^[2]   ---定義--- 用n表示圖中頂點數目，用e表示邊或弧的數目。若<vi,vj>∈VR，則vi≠vj，那麼，對於 無向圖，e的取值範圍是0到，有條邊的無向圖稱為 完全圖。 ---解釋--- 直觀來說，若一個圖中每條邊都是無方向的，則稱為 無向圖。 （1）無向邊的表示 無向圖中的邊均是頂點的無序對，無序對通常用圓括號表示。 【例】無序對(vi，vj)和(vj，vi)表示同一條邊。 （2）無向圖的表示 【例】下面(b)圖中的G2和(c)圖中的G3均是無向圖，它們的頂點集和邊集分別為： V(G2)={v1，v2，v3，v4} E(G2)={(vl，v2)，(v1，v3)，(v1，v4)，(v2，v3)，(v2，v4)，(v3，v4)} V(G3)={v1，v2，v3，v4，v5，v6，v7} E(G3)={(v1，v2)，(vl，v3)，(v2，v4)，(v2，v5)，(v3，v6)，(v3，v7)}
---注意--- 在以下討論中，不考慮頂點到其自身的邊。即若(v1，v2)或<vl，v2>是E(G)中的一條邊，則要求v1≠v2。此外，不允許一條邊在圖中重複出現，即只討論簡單的圖。