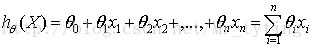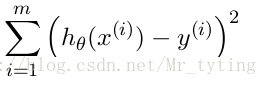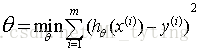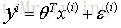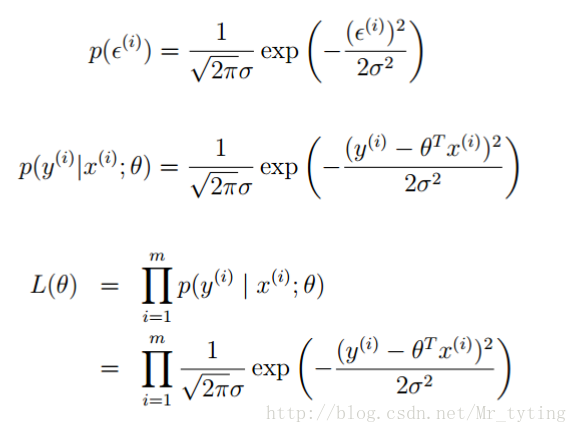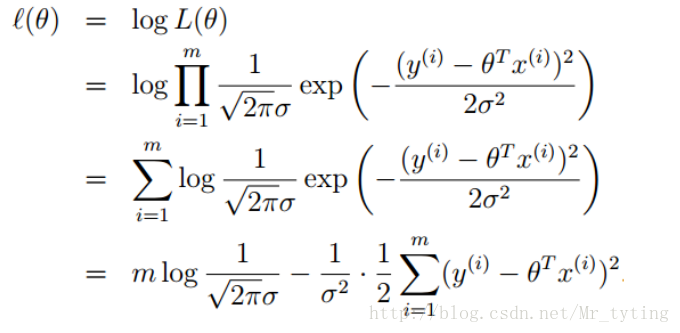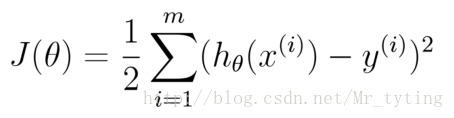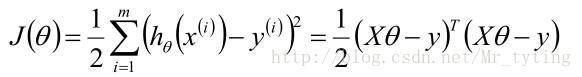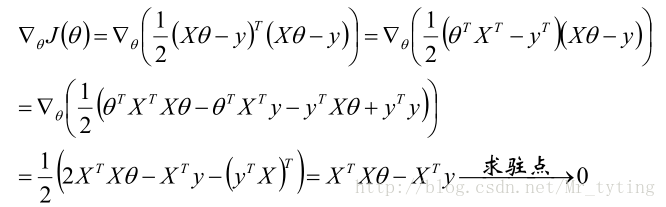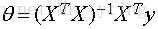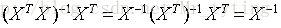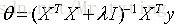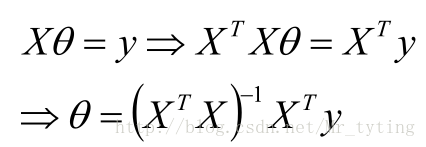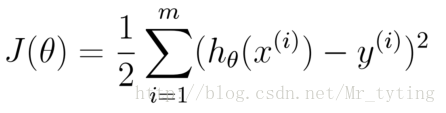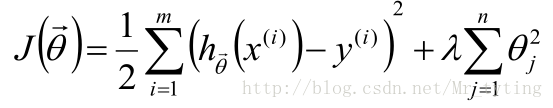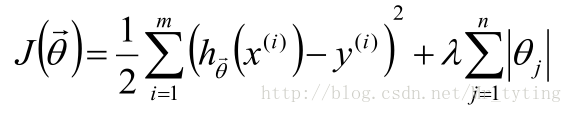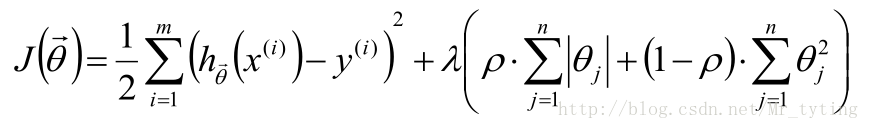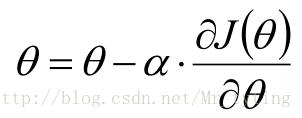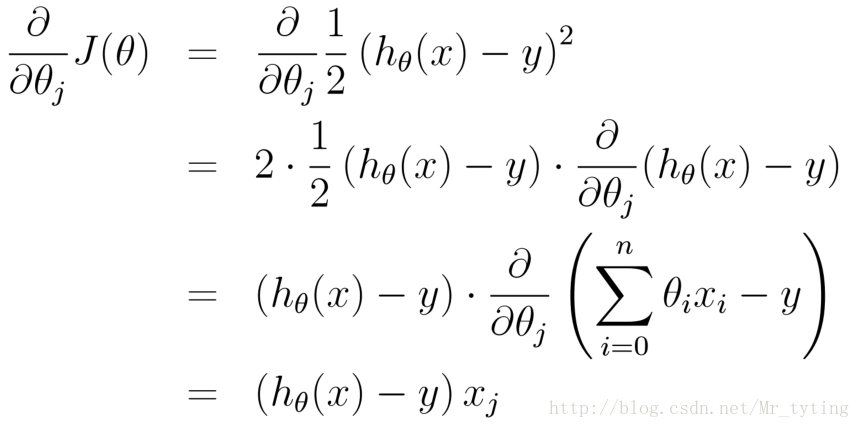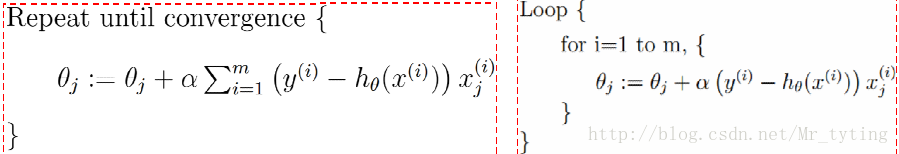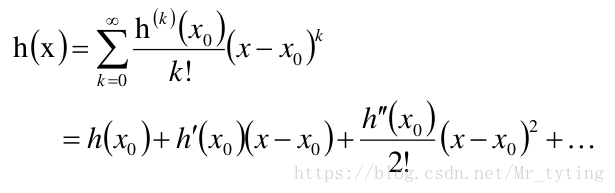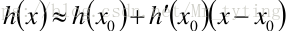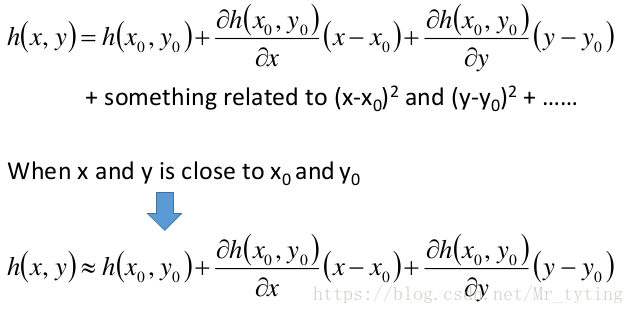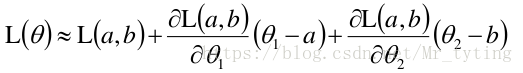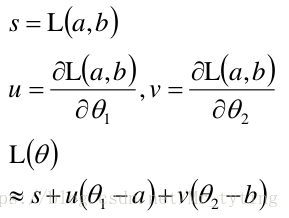機器學習->監督學習->線性迴歸(LASSO,Ridge,SGD)
本篇博文主要總結線性迴歸,線性迴歸雖然簡單,但是卻是很重要,我將沿著以下幾個主題總結
- 最小二乘法
- 使用極大似然估計來解釋最小二乘
的解析式的求解過程
- 線性迴歸的複雜度懲罰因子(LASSO,Ridge)
- 梯度下降法
- 實戰
最小二乘法
線性迴歸,線性是指回歸方程在空間中表現為直線形式,其決策邊界是線性的.迴歸在數學上來說是給定一個點集,能夠用一條曲線去擬合之,如果這個曲線是一條直線,那就被稱為線性迴歸,
基本形式:
給定資料集”線性迴歸”試圖學得一個線性模型以儘可能地預測實際輸出值.這個不斷學習的過程實際上就是不斷調整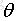
然而有一個問題,在這個學習過程中如何評價衡量他學習的效果?因此我們需要定義一個損失函式
均方誤差是迴歸任務中最常用的效能度量,因此我們可以試圖讓均方誤差最小化.
cost Function:
學習的目標:
均方誤差有非常好的幾何意義,類似與常用的歐幾里得距離.基於均方誤差最小化的進行模型求解方法稱為”最小二乘法“(least square method),線上性迴歸中,最小二乘法就是找到一條直線,使所有樣本到直線的距離之和最小.
使用極大似然估計來解釋最小二乘
上面公式中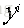
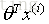
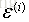
誤差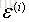
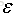
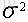
似然函式
上面說了誤差服從高斯分佈,那麼可得:
再求最大似然函式:
我們要求出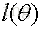
這樣我們就通過了最大似然估計來解釋了最小二乘估計的由來,其實最小二乘估計就是假定誤差服從高斯分佈,認為樣本是獨立,使用最大似然估計就能得出的結論。
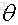 的解析式的求解過程
的解析式的求解過程
將M個N維樣本組成矩陣X:
- X的每一行對應一個樣本,共M個樣本(measurements)
- X的每一列對應樣本的一個維度,共N維(regressors)
- 還有額外的一維常數項,全為1
那麼目標函式:
梯度:
關於矩陣如何求導請看我的另外一篇博文機器學習–>矩陣和線性代數裡面相關內容。
那麼可得引數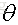
若X為可逆矩陣,則有:
因此可以定義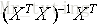
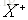
由此可以推出: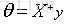
對於m*n的矩陣X,若它的SVD分解為: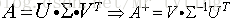
若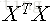
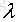
可以如下的簡便記憶:
線性迴歸的複雜度懲罰因子(LASSO,Ridge)
線性迴歸的目標函式為:
為了防止引數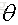
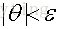
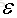
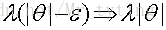
那麼加上不同的正則項來防止過擬合:
Ridge:在目標函式後加上L2正則項:
LASSO:在目標函式後加上L1正則項:
ELastic Net:L1正則項與L2正則項混合使用:
那麼在目標函式後面加上正則項,正則項就是關於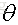
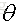
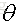
我們在訓練一個線性模型時,這個模型越簡單越好,就是希望引數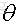
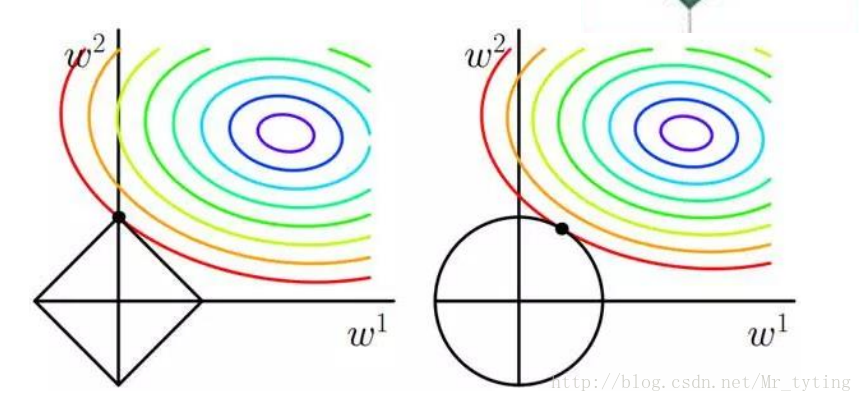
對比L1正則化和L2正則化,來看看為什麼L1正則化能使引數變得稀疏。
這裡假設目標函式裡面只有兩個引數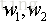
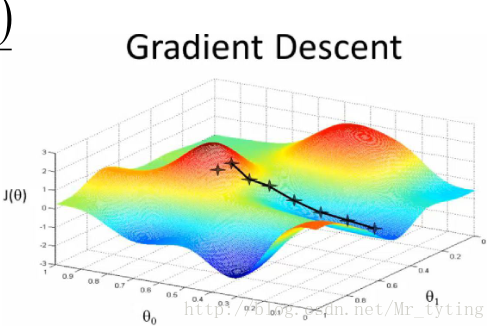
梯度下降法
在實際情景中,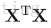
於是我們要用一種逼近的辦法來求解引數:梯度下降法.
梯度下降法一般流程:
- 首先對引數賦值,這個值可以是隨機的,也可以
讓是一個全零的向量.
改變
的值,使其損失函式按照梯度下降的方向進行減少,這個方向其實就是減少最快的方向
這時目標函式是關於引數的函式,需要不斷的沿著引數的梯度方向下降,才能到達最低點。
- 不斷重複2)步驟,使其誤差在給定範圍內.
梯度方向:
這裡需要注意:當我們以損失函式進行引數估計時(例如線性迴歸裡面的最小二乘估計),因為是求損失函式最小時的引數(是一個不斷下降地逼近最低值),故採用梯度下降法,當我們用最大似然函式進行引數估計時,是求似然函式最大時對應的引數(是一個不斷上升地逼近最高值),那麼這時時梯度上升法。其實道理都是一樣,只是前面正負號的問題。
批量梯度下降演算法(GD):每次迭代拿出所有樣本來更新引數
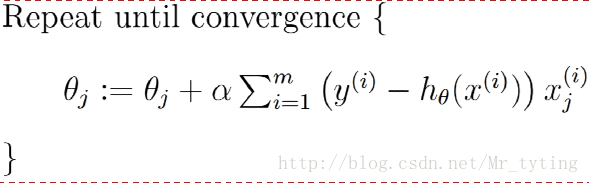
凸函式肯定能利用批量梯度下降法達到全域性最優值(前提選擇合適學習速率)
隨機梯度下降演算法(SGD):每次迭代隨機拿出一個樣本來更新引數
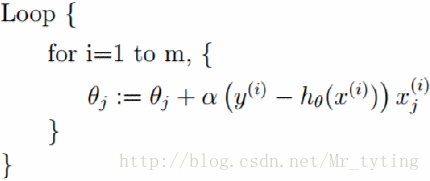
有時候隨機梯度下降法比起批量梯度下降法更不容易陷入區域性最優。
折中:mini-batch(mini-batchGD):每次迭代隨機拿出一部分樣本來更新引數
現在一般把mini-batchGD直接叫做SGD。
一步步更新w,b,一步步的迭代,那麼這個更新迭代的過程什麼時候結束呢?通常採用以下辦法來判斷什麼時候停止更新迭代
1)定義一個最大迭代步數,當迭代次數大於等於這個最大迭代步數時,停止迭代
2)定義一個最小誤差,當你更新得到的w,b代入到均方誤差中得出的誤差小於定義的最小誤差,則停止迭代。
從泰勒公式解釋隨機梯度下降法
我們知道對於一個連續函式,在可導的某點處,都可以展開近似,逼近。
顯然,當 很接近 時:
同理多變數的泰勒展開式:
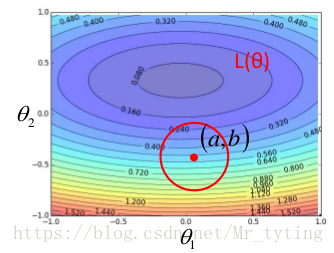
回到機器學習中的,我們假設該 只有兩個引數決定,分別是。則 的等高線可如下:
那麼在點(a,b) 處,我們可以利用泰勒展式來逼近。
注意:上式中的約等於號要成立,則點 必須在點 附近,兩點距離越近越相等。
好了,我們得到了 的公式,希望能:
上式中的 與 無關,可以忽略,那麼有:
將其看成向量內積的形式,則在最小化 時有:
取向量 的反方向,但是其向量長度不能太大,我們需要保證其距離向量 較近的地方,這樣其上面的約等於號才能成立。
最後需要注意一點:線性迴歸可以是對樣本非線性的,只要是對引數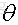
例如: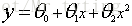
實戰:
根據以上所學的我們來做一道題:
預測2014年南京市的房價,下面給出其歷史資料:
Year X=[2000,2001,2002,2003,2004,2005,2006,2007,2008,2009,2010,2011,2012,2013]
Price Y=[2.000,2.500,2.900,3.147,4.515,4.903,5.365,5.704,6.853,7.971,8.561,10.000,
11.280,12.900]
這裡寫程式碼片
#coding:utf-8
import numpy as np
def geData():
X=[0,1,2,3,4,5,6,7,8,9,10,11,12,13]
Y=[2.000,2.500,2.900,3.147,4.515,4.903,5.365,5.704,6.853,7.971,8.561,10.000,11.280,12.900]
points=np.array((X,Y)).T
return points
def errors(w,b,points):
totalError=0
for i in range(0,len(points)):
x=points[i,0]
y=points[i,1]
totalError+=(y-(w*x+b))**2
return totalError
def step_gradient(b_current,w_current,points,alpha):
b_gradient=0
w_gradient=0
N=float(len(points))
for i in range(0,len(points)):
x=points[i,0]