圖解機器學習-監督學習-線性迴歸總結
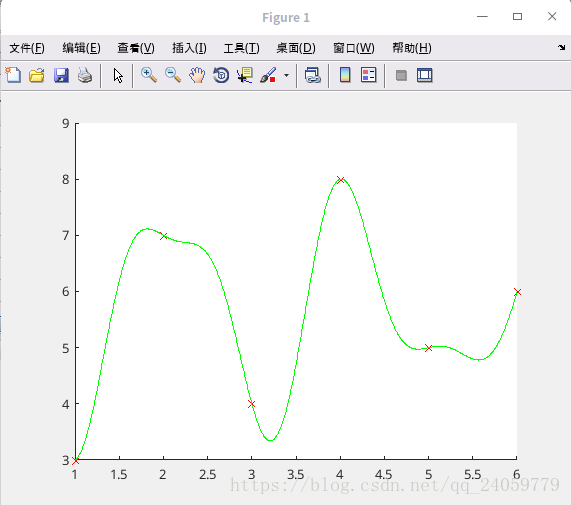
code:1.分析資料需要用什麼函式來擬合,給定已知sin函式的時候好擬合,但是未知函式是幾次,未知具體函式什麼樣子的時候擬合的時候需要自己觀察資料,並選擇相應的模型擬合,我自己編寫了一段code,擬合一下試試演算法的實用性.
x=[1,3,5,6,2,4]'; y=[3,4,5,6,7,8]'; plot(x,y,'rx'); plot(x,y,'rx'); %沿著x增大的方向模擬幾個點的線,看情況有點像書上的sin函式cos函式的交替,試一試 X=linspace(1,6,1000)'; p(:,1)=ones(6,1);P(:,1)=ones(1000,1); for j=1:15 p(:,2*j)=sin(j/2*x);p(:,2*j+1)=cos(j/2*x); P(:,2*j)=sin(j/2*X);P(:,2*j+1)=cos(j/2*X); end t=p\y; F=P*t; figure(1);clf;hold on; plot(x,y,'rx'); plot(X,F,'g-');
矩陣的奇異值分解具體請見blog: https://www.cnblogs.com/lzllovesyl/p/5243370.html
正交投影見blog:https://blog.csdn.net/tengweitw/article/details/41174555
正交投影約束條件中的P矩陣需要用到pca:第13章,第17章一起看了,看看這個
http://blog.codinglabs.org/articles/pca-tutorial.html
簡單總結一下PCA:在某種合理的情況下資料降維可以大大減少運算時間和記憶體空間,但是這種降維度方式必須是合理的,例如上文中的兩個事例-淘寶店和男性女性就是為了說明資料降維不是隨便的,在資料相關性,資料依賴性比較強的資料之間可以降維
同理主成分分析法在降維時也必須有合理性--
A與B的內積,等於A在B方向上的投影乘B標量向量長度,
要描述一個向量,首先要確定一組基向量,然後給出在各個直線上的投影值.
從內積的定義可以看到,如果基底(B)的模是1,那麼就可以方便的用向量點乘基而直接獲得在其新基上的座標.
基底變換可以用矩陣表示,假設由m個n維向量組成(n*m)矩陣X,現在用n維空間中的r個正交向量積來左乘,如下圖,就達到了降緯的效果,可以看到原本a1表示的是n維度的座標值,現在被換算成左邊一豎列R維度的座標值,由原來的n維度降低到了r維度,一切都歸功於在原座標系原維度的m個n維矩陣左邊乘了該空間中不滿秩的正交向量基.

現在要解決R的維數怎麼取,降維到什麼空間能夠保證資料儲存最完整的前提下縮減時間空間複雜度.上文中舉了一個二維降到一維的例子.
一條直線上點的方差可以表示為:每一個點對均值做差再平方,然後把這些值加起來.當這個和值越大,說明分開的效果越好,資料獨立性越好,不存在重複的資料.
將一組n維資料降為k維,目標是選擇k個單位正交基,使得原始資料變換到這組基上後,各欄位兩兩協方差為0,而欄位間的儘可能大,
x*x' !
將協方差矩陣對角化:即除對角線外的其它元素化為0,並且在對角線上將元素按大小從上到下排列,這樣我們就達到了優化目的
尋找一個矩陣P,滿足PCPTPCPT是一個對角矩陣,並且對角元素按從大到小依次排列,那麼P的前K行就是要尋找的基,用P的前K行組成的矩陣乘以X就使得X從N維降到了K維並滿足上述優化條件。
P是協方差矩陣的特徵向量單位化後按行排列出的矩陣,其中每一行都是C的一個特徵向量。如果設P按照ΛΛ中特徵值的從大到小,將特徵向量從上到下排列,則用P的前K行組成的矩陣乘以原始資料矩陣X,就得到了我們需要的降維後的資料矩陣Y。
https://zhuanlan.zhihu.com/p/30145700
這篇部落格講解了PCA中k值的取值什麼時候是合理的,在k取不同值的時候對真實資料儲存比例.
對書中正交對映限制引數問題程式碼的理解:
其實
x=linspace(-3,3,50)';
X=linspace(-3,3,1000)';
for i=1:7
p(:,i)=x.^(i-1);
P(:,i)=X.^(i-1);
end
t1=p\y;
t2=(p*diag([1,1,1,0,0,0,0]))\y;
f1=P*t1;
f2=P*t2;
figure(1);clf;hold on; plot(x,y,'rx');plot(X,f1,'g-');
figure(2);clf;hold on; plot(x,y,'rx');plot(X,f2,'g-');
這部分對P的取值和後面的PCA技術相關性不是太大,舉個簡單的例子,在我已知一個由二次函式構造的函式樣本,前幾次我用6次的多項式函式去模擬函式,可以的到如圖所示的所示

當我用P正交法,用其乘一個對角化矩陣,把其降維,不但可以節省運算的時間複雜度,更能夠使得過擬合問題得到解決,好處太多

這兩個圖別看這一樣,放大之後一頓切換明顯能看到第一個6次複雜度的過擬合.2次的方程沒毛病.
這第一個正交化的程式碼的含義就是簡單的把過擬合過估計的部門引數抹掉,解決過擬合,引數複雜度過多的問題.
L2約束的最小二乘學習法:
P的使用實在是太扯淡了,自己隨便改,根本不是按照pca來的,只是稍微使用了pca裡面的矩陣降維的思想.所以實際中使用L2的約束條件比較好,
學習拉格朗日對偶原理重要的是理解構造所得的原始問題和原函式的等價性,以及原始問題和對偶問題解得等價性
https://www.cnblogs.com/90zeng/p/Lagrange_duality.html
kernal fuction是比較好,方法比較通用,但是你得很好的擬合啊,那引數hh能夠隨便設定麼,得需要一遍一遍試才可以吧.所以針對簡單的二次函式,擬合效果不用想,肯定很差,但是還要試試吧.

樣本點只取5個點,擬合成了什麼樣子了都

所以所有人都在強調,大資料的重要性,當樣本數為50的時候,擬合的明顯就好的很多很多,但是很容易發現,這種擬合屬於過度擬合,在五十個樣本比較集中地地方擬合的非常好,但是在邊緣部分,因為樣本分佈越來越稀疏,可以發現對未知樣本點的預測能力極差,影象和點完全不擬合,所以需要使用接下來介紹的防止過擬合的約束條件進行阻止過擬合,讓樣本在未知的領域具有較強的預測能力
x=[-2,-1,0,1,2]';
>> y=x.^2;
>> p(:,2)=x;
>> p(:,1)=1;
>> p(:,3)=x.^2;
>> t0=rand(3,1);
>> e=0.1;
for o=1:1000
i=ceil(rand*5);
k=p(i,:);
t=t0-e*k'*(k*t0-y(i));
if (t-t0)<0.001,break,end
t0=t;
end
X=linspace(-3,3,1000)';
>> P(:,2)=X;
>> P(:,1)=1;
>> P(:,3)=X.^2;
>> F=P*t;
>> figure(1);clf;hold on;
>> plot(x,y,'rx');
>> plot(X,F,'g-');
程式碼段2:
x=linspace(-3,3,50)';
y=x.^2;
X=linspace(-3,3,1000)';
hh=2*0.3^2;t0=rand(50,1);e=0.1;
for o=1:1000
i=ceil(rand*50);
ki=exp(-(x-x(i)).^2/hh);
t=t0-e*ki*(ki'*t0-y(i));
if norm(t-t0)<0.001,break,end
t0=t;
end
K=exp(-(repmat(X.^2,1,50)+repmat(x.^2',1000,1)-2*X*x')/hh);
>> F=K*t;
>> figure(1);clf;hold on;
>> plot(x,y,'rx');
>> plot(X,F,'g-');L2約束條件的最小二乘法
原始碼:
x=[1,3,5,6,2,4]';
y=[3,4,5,6,7,8]';
plot(x,y,'rx');
plot(x,y,'rx');
%沿著x增大的方向模擬幾個點的線,看情況有點像書上的sin函式cos函式的交替,試一試
X=linspace(1,6,1000)';
p(:,1)=ones(6,1);P(:,1)=ones(1000,1);
for j=1:15
p(:,2*j)=sin(j/2*x);p(:,2*j+1)=cos(j/2*x);
P(:,2*j)=sin(j/2*X);P(:,2*j+1)=cos(j/2*X);
end
t=p\y;
F=P*t;
figure(1);clf;hold on;
plot(x,y,'rx');
plot(X,F,'g-');
t2=(p'*p+0.1*eye(31))\p'*y;
>> F2=P*t2;
>> figure(2);clf;hold on;plot(x,y,'rx');plot(X,F2,'g-');

雖然不太好講,但是也要強行解釋一波,確實對過去的過擬合問題得到了很大程度的改善,但是這個影象的變化太劇烈了,我再去試試二次函式的那個看看效果是什麼樣子,希望不會影象不會有太大的變化,beg
x=linspace(-3,3,50)';
y=x.^2;
X=linspace(-3,3,1000)';
hh=2*0.3^2;t0=rand(50,1);
k1=exp(-(repmat(x.^2,1,50)+repmat(x.^2',50,1)-2*x*x')/hh);
K1=exp(-(repmat(X.^2,1,50)+repmat(x.^2',1000,1)-2*X*x')/hh);
t1=k1\y;
F1=K1*t1;
t2=(k1^2+0.1*eye(50))\k1*y;
F2=K1*t2;
figure(1);clf;hold on;plot(x,y,'rx');plot(X,F1,'g-');
figure(2);clf;hold on;plot(x,y,'rx');plot(X,F2,'g-');

這個還不是比較明顯的,因為我模擬的二次函式是沒有噪聲的二次函式,只能看出來確實圖二擬合的效果沒有圖一好,下面選取有噪聲的二次函式模擬一下
原始碼:
x=linspace(-3,3,50)';
y=x.^2+rand(50,1);
X=linspace(-3,3,1000)';
hh=2*0.3^2;t0=rand(50,1);e=0.1;
k1=exp(-(repmat(x.^2,1,50)+repmat(x.^2',50,1)-2*x*x')/hh);
K1=exp(-(repmat(X.^2,1,50)+repmat(x.^2',1000,1)-2*X*x')/hh);
t1=k1\y;
F1=K1*t1;
t2=(k1^2+0.1*eye(50))\k1*y;
F2=K1*t2;
figure(1);clf;hold on;axis([-3 3 -10 10]);plot(x,y,'rx');plot(X,F1,'g-');
figure(2);clf;hold on;axis([-3 3 -10 10]);plot(x,y,'rx');plot(X,F2,'g-');

可以看出來:當擬合具有噪聲的二次函式的時候圖一已經有過擬合的效果了,這樣對以後的預測會產生很大的誤差,圖二使用L2約束的最小二乘法不但使影象更趨於平滑而且減弱了過擬合問題.
模型選擇:
涉及到高斯kenal函式的模型引數選擇書上給出了相應的方法:交叉驗證法:
1把訓練樣本隨機分成m個集合(2-10之間),大小一致
2.對i=1....m迴圈執行如下操作
(a).對除了第i組的其餘樣本進行學習得到學習結果fi
(b).把上述沒有參加訓練的樣本作為測試集,對上面的fi進行泛化誤差評估,評估函式書上有
3.對各個i的泛化誤差的評估值進行平均,得到最終的泛化誤差評估值,選擇最小的泛化誤差評估值對應的引數為最合適的引數
對上面我的二次函式試一試到底什麼樣的高斯引數才是能夠最好擬合的呢?
求矩陣A的最大值的函式有3種呼叫格式,分別是:
(1) max(A):返回一個行向量,向量的第i個元素是矩陣A的第i列上的最大值。
(2) [Y,U]=max(A):返回行向量Y和U,Y向量記錄A的每列的最大值,U向量記錄每列最大值的行號。
(3) max(A,[],dim):dim取1或2。dim取1時,該函式和max(A)完全相同;dim取2時,該函式返回一個列向量,其第i個元素是A矩陣的第i行上的最大值。
x=linspace(-3,3,50)';
y=x.^2+rand(50,1);
X=linspace(-3,3,1000)';
hhs=2*[0.03 0.3 3].^2;
ls=[0.0001 0.001 0.1];
s=repmat(x.^2,1,50)+repmat(x.^2',50,1)-2*x*x';
u=floor([0:49]/10)+1;
u=u(randperm(50));
for hk=1:length(hhs)
hh=hhs(hk);k=exp(-s/hh);
for i=1:5
ki=k(u~=i,:);kc=k(u==i,:);yi=y(u~=i);yc=y(u==i);
for lk=1:length(ls)
l=ls(lk);
t=(ki'*ki+l*eye(50))\(ki'*yi);fc=kc*t;
g(hk,lk,i)=mean((fc-yc).^2);
end,end,end
[gl,ggl]=min(mean(g,3),[],2);
[ga,gb]=min(gl);
l=ls(ggl(gb));
hh=hhs(gb);
k=exp(-s/hh);
K=exp(-(repmat(X.^2,1,50)+repmat(x.^2',1000,1)-2*X*x')/hh);
t=(k^2+l*eye(50))\(k*y);
F=K*t;
figure(1);clf;hold on;plot(x,y,'rx');plot(X,F,'g-');
明顯看到在這份引數下二次函式擬合的效果達到更好,更加平滑
l1約束原始碼:
x=linspace(-3,3,50)';
y=x.^2+rand(50,1);
X=linspace(-3,3,1000)';
hh=2*0.3^2;t0=rand(50,1);e=0.1;
k1=exp(-(repmat(x.^2,1,50)+repmat(x.^2',50,1)-2*x*x')/hh);
K1=exp(-(repmat(X.^2,1,50)+repmat(x.^2',1000,1)-2*X*x')/hh);
t1=k1\y;
F1=K1*t1;
for o=1:1000
t2=(k1^2+e*pinv(diag(abs(t0))))\k1*y;
if (t2-t0)<0.001,break,end
t0=t2;
end
F2=K1*t2;
figure(1),clf;hold on;plot(x,y,'rx');axis([-3 3 0 10]);plot(X,F1,'g-');
figure(2),clf;hold on;plot(x,y,'rx');plot(X,F2,'g-');

效果不比之前差,最關鍵的是這個l1約束條件下面得到的引數是稀疏,很多0,計算的時間複雜度明顯縮小:

可以看到一共50個引數,有一半的引數都是0.
l無窮範數表示的是引數裡面的最大值
l0範數表示的是引數裡面的非0元素的個數
l1+l2範數約束的最小二乘法:

原始碼:
x=linspace(-3,3,50)';
y=x.^2+rand(50,1);
X=linspace(-3,3,1000)';
hh=2*0.3^2;t0=rand(50,1);e=0.1;
k1=exp(-(repmat(x.^2,1,50)+repmat(x.^2',50,1)-2*x*x')/hh);
K1=exp(-(repmat(X.^2,1,50)+repmat(x.^2',1000,1)-2*X*x')/hh);
t1=k1\y;
F1=K1*t1;
for o=1:1000
t2=(k1^2+e*pinv(diag(abs(t0))))\k1*y;
if (t2-t0)<0.001,break,end
t0=t2;
end
t3=(k1^2+e*eye(50))\k1*y;
t4=t2/2+t3/2;
F2=K1*t2;
F3=K1*t3;
F4=K1*t4;
figure(1),clf;hold on;plot(x,y,'rx');axis([-3 3 0 10]);plot(X,F1,'g-');
figure(2),clf;hold on;plot(x,y,'rx');plot(X,F2,'g-');
figure(3),clf;hold on;plot(x,y,'rx');plot(X,F3,'g-');
figure(4),clf;hold on;plot(x,y,'rx');plot(X,F4,'g-');




具體效果需要全屏切換觀察,具體效果的好壞仁者見仁智者見智,我以後會使用l1和l2結合的最小二乘法來進行計算.
魯棒學習:
https://mp.csdn.net/postedit/82763849
使用l2損失最小化學習異常值會使得殘差平方和劇增所以要使用殘差和線性增長的l1損失最小函式來驗證訓練樣本的合理性,對不合理的樣本予以剔除掉.但是l1絕對值魯棒學習法有一個很明顯的缺點就是不能求導,要藉助於變化成為二次函式之後才能求導,而且高的魯棒性與學習模型並不十分吻合,為0的時候會得到最好的魯棒性,實際學習效果旺旺並不能達到預期,所以為了能夠很好的取得有效性和魯棒性的平衡發明huber演算法,l2的部分是使得模型更貼近樣本,l1的部分是為了使得它有更好的魯棒性.
有效果有效果 原始碼:
x=linspace(-4,4,10)';
X=linspace(-4,4,1000)';
y=x+0.2*randn(10,1);
y(1)=-8;y(8)=9;y(4)=-9;y(3)=18;
p(:,1)=ones(10,1);
p(:,2)=x;
P(:,1)=ones(1000,1);P(:,2)=X;
t1=p\y;
F1=P*t1;
e=1;
for o=1:1000
r=abs(p*t1-y);
w=ones(10,1);
w(r>e)=e./r(r>e);
t2=(p'*(repmat(w,1,2).*p))\(p'*(w.*y));
if norm(t2-t1)<0.001,break,end
t1=t2;
end
F2=P*t2;
figure(1),clf;hold on;plot(x,y,'rx');plot(X,F1,'g-');
figure(2),clf;hold on;plot(x,y,'rx');plot(X,F2,'g-');


圖基:
x=linspace(-4,4,10)';
X=linspace(-4,4,1000)';
y=x+0.2*randn(10,1);
y(8)=9;y(4)=-9;
p(:,1)=ones(10,1);
p(:,2)=x;
P(:,1)=ones(1000,1);P(:,2)=X;
t1=p\y;
e=1;
for o=1:1000
r=abs(p*t1-y);
w=zeros(10,1);
w(r<=e)=(1-r(r<=e).^2/e^2).^2;
t2=(p'*(repmat(w,1,2).*p))\(p'*(w.*y));
if norm(t2-t1)<0.001,break,end
t1=t2;
end
F1=P*t2;
>> t3=p\y;
>> for o=1:1000
r=abs(p*t3-y);
w=ones(10,1);
w(r>e)=e./r(r>e);
t4=(p'*(repmat(w,1,2).*p))\(p'*(w.*y));
if norm(t4-t3)<0.001,break,end
t3=t4;
end
>> F2=P*t4;
>> figure(1),clf;hold on;plot(x,y,'rx');plot(X,F1,'g-');
>> figure(2),clf;hold on;plot(x,y,'rx');plot(X,F2,'g-');

圖基演算法明顯效果比huber還要好,但是要注意的一點是,圖基演算法的初始值一定要是對的,初始值錯了,演算法基本就崩潰了,什麼奇異值精確度的報錯;
rand('state',0);randn('state',0);
n=50;N=1000;x=linspace(-3,3,n)';X=linspace(-3,3,N)';
pix=pi*x;y=sin(pix)+0.1*x+0.2*randn(n,1);
y(n/2)=-0.5;
hh=2*0.3^2;l=0.1;e=0.1;
k=exp(-(repmat(x.^2,1,n)+repmat(x.^2',n,1)-2*x*x')/hh);
t1=k\y;
K=exp(-(repmat(X.^2,1,n)+repmat(x.^2',N,1)-2*X*x')/hh);
F1=K*t1;
for o=1:100
end
t0=randn(n,1);
for o=1:100
t=(k^2+l*pinv(diag(abs(t0))))\(k*y);
if norm(t-t0)<0.001,break,end
t0=t;
end
F2=K*t;
t3=k\y;
for o=1:100
r=abs(k*t3-y);w=ones(n,1);w(r>e)=e./r(r>e);
t2=(k'*(repmat(w,1,50).*k))\(k'*(w.*y));
Z=k*(repmat(w,1,n).*k)+l*pinv(diag(abs(t3)));
t4=(Z+0.00001*eye(n))\(k*(w.*y));
if norm(t4-t3)<0.001,break,end
t3=t2;
t3=t4;
end
F3=K*t2;
F4=K*t4;
figure(1),clf;hold on;plot(x,y,'rx');plot(X,F1,'g-');
figure(2),clf;hold on;plot(x,y,'rx');plot(X,F2,'g-');
figure(3),clf;hold on;plot(x,y,'rx');plot(X,F3,'g-');
figure(4),clf;hold on;plot(x,y,'rx');plot(X,F4,'g-');



分析:
圖一沒有處理過的線過擬合受異常值干擾嚴重
圖二的l1約束後明顯解決了過擬合的問題,但是仍然受異常值影響嚴重
圖三單單使用huber來擬合可以解決魯棒性的問題即受異常值的影響較小,但是不能解決過擬合的問題
圖四使用huber+l1約束,,能夠很好的解決過擬合和魯棒性的問題