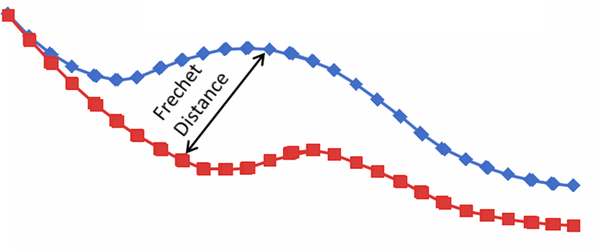
Fréchet distance(弗雷歇距離)是法國數學家Maurice René Fréchet在1906年提出的一種路徑空間相似形描述( 此外還在這篇論文裡定義了 度量空間)，這種描述同時還考慮進路徑空間距離的因素[1]，對於空間路徑的相似性比較適用。

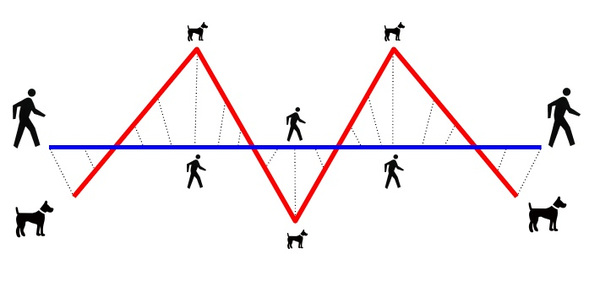
直觀的理解，Fréchet distance就是狗繩距離：主人走路徑A，狗走路徑B，各自走完這兩條路徑過程中所需要的最短狗繩長度。

嚴格的數學定義如下：

設二元組是一個度量空間，其中是上的度量函式.

1. 在單位區間上的對映是連續對映，則稱為上的連續曲線。

2. 從單位區間到其自身的對映，滿足如下三個條件：1)是連續的，2)是非降的，即對於任意

3. 設和是 上的兩條連續曲線，即，. 又設 α 和 β 是單位區間的兩個重引數化函式，即 ，. 則曲線與曲線的弗雷歇距離定義為

其中是上的度量函式.

數字化/離散化

設定是時間點，該時刻，曲線上的取樣點為, 曲線上取樣點為. 如果使用歐氏距離，則容易定義. 在每次取樣中離散的遍歷區間, 得到該種取樣下的最大距離. 弗雷歇距離就是使該最大距離最小化的取樣方式下的值。

易於理解的，在離散方式下，我們不可能得到真實的弗雷歇距離，而可以無限的趨近。但是越精確的值需要越大的計算量。

基於該離散思想，對應的兩條空間(3D)路徑弗雷歇距離matlab程式碼如下：

%% Frechet Distance between two curves (3D)

%%

functionf =frechet3D(P1,P2,varargin)

X1=P1(:,1);

X2=P2(:,1);

Y1=P1(:,2);

Y2=P2(:,2);

Z1=P1(:,3);

Z2=P2(:,3);

%get path point length

L1=length(X1);

L2=length(X2);

%check vector lengths

if or(L1~=length
 
(Y1),L2~=length(Y2))

    error('Paired input vectors (Xi,Yi) must be the same length.')

end

%check for column inputs

if or(or(size(X1,1)<=1,size(Y1,1)<=1),or(size(X2,1)<=1,size(Y2,1)<=1))

    error('Input vectors must be column vectors.')

end

%create maxtrix forms

X1_mat=ones(L2,1)*X1';

Y1_mat=ones(L2,1)*Y1';

Z1_mat=ones(L2,1)*Z1';

X2_mat=X2*ones(1,L1);

Y2_mat=Y2*ones(1,L1);

Z2_mat=Z2*ones(1,L1);

%calculate frechet distance matrix

frechet1=sqrt((X1_mat-X2_mat).^2+(Y1_mat-Y2_mat).^2+(Z1_mat-Z2_mat).^2);

fmin=min(frechet1(:));

fmax=max(frechet1(:));

%handle resolution

if ~isempty(varargin)

    res=varargin{1};

    if res<=0

        error('The resolution parameter must be greater than zero.')

    elseif ((fmax-fmin)/res)>10000

        warning('Given these two curves, and that resolution, this might take a while.')

    elseif res>=(fmax-fmin)

        warning('The resolution is too low given these curves to compute anything meaningful.')

        f=fmax;

        return

    end

else

    res=(fmax-fmin)/100;

end

%compute frechet distance

clear f

for q3=fmin:res:fmax

    im1=bwlabel(frechet1<=q3);

%get region number of beginning and end points

    if and(im1(1,1)~=0,im1(1,1)==im1(end,end))

        f=q3;

        break

    end

end

if (~(exist ('f')))

    f=fmax;

end

% disp(f)

return

--------

[1] Fréchet, M. Maurice. "Sur quelques points du calcul fonctionnel." Rendiconti del Circolo Matematico di Palermo (1884-1940) 22.1 (1906): 1-72.