決策樹學習 -- ID3演算法和C4.5演算法(C++實現)
前言
在學習西瓜書的時候,由於書本講的大多是概念,所以打算用C++實現它的演算法部分(至於python和matlab實現,實現簡單了很多,可以自己基於C++程式碼實現)。至於測試資料,採用了書中關於西瓜的資料集。
什麼是決策樹
首先,決策樹(也叫做分類樹或迴歸樹)是一個十分常用的分類方法,在機器學習中它屬於監督學習的範疇。由於決策樹是基於樹結構來決策的,所以學習過資料結構的人,相對來說會比較好理解。
一般的,一顆決策樹包含一個根結點,若干個內部結點和若干個葉結點;葉子結點對應於決策結果,其他每個結點則對應一個屬性測試;每個結點包含的樣本集合根據屬性測試的結果被劃分到子結點中;根節點包含樣本全集。從根結點到每個葉結點的路徑對應了一個判定測試序列。決策樹學習的目的是為了產生一顆泛化能力強,即處理未見示例能力強的決策樹,其基本流程遵循簡單且直觀的“分而治之”策略。(《機器學習(周志華)》)
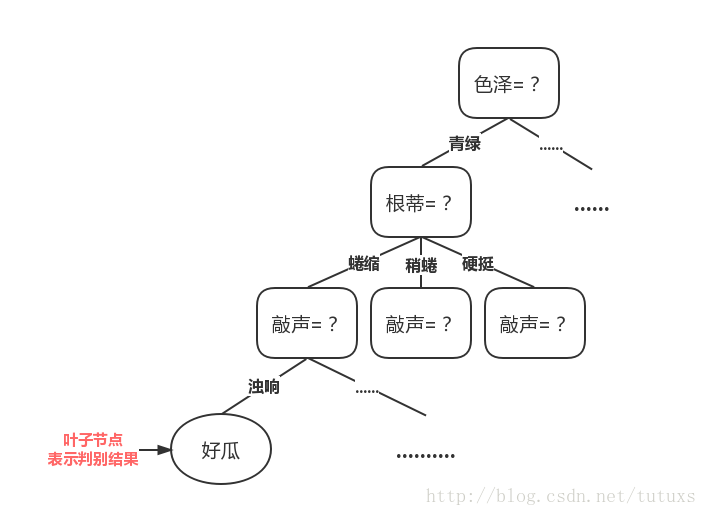
例如:書中的關於西瓜問題的一顆決策樹
從這個圖可以看出,色澤青綠,根蒂蜷縮,敲聲濁響的西瓜為好瓜
關鍵在於哪裡?
隨著劃分過程不斷進行,我們希望決策樹的分支結點所包含的樣本儘可能屬於同一類別,即結點的“純度”越來越高。這句話的意思是說,在樹的相同層裡,要麼好瓜這一類別越多越好,要麼壞瓜這一類別越多越好。
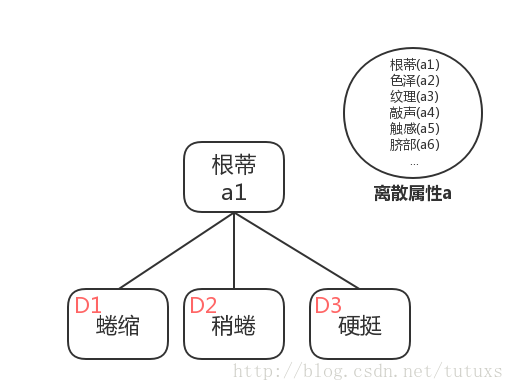
例如上圖中,西瓜根蒂的分類有:蜷縮,稍蜷和硬挺。
這裡可以打一個比方:足球比賽中,一般會把多個球隊分在同一個小組,如果一個小組中的各支球隊實力都相當,那麼小組出線的可能性就難於預測,如果各個球隊的實力差距相當懸殊,那麼實力較強的球隊出線的可能性會相當大。
同樣的道理我們希望每一個分支下面的類別(即好瓜和壞瓜)儘可能屬於同一類別,如果同一類別更多,換句話說就是該類別實力比較強,依據該屬性(根蒂)
基本概念
資訊熵(information entropy)
在資訊理論與概率統計中,熵是表示隨機變數不確定性的度量,熵越大,隨機變數的不確定性就越大。資訊熵是度量樣本集合“純度”最常用的一種指標。假定當前樣本集合D中第k類樣本所佔比例為
注意:
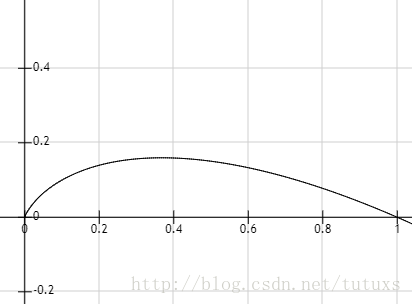
由
當超過0.4的時候,隨著
結論:Ent(D)的值越小,則D的純度越高
資訊增益(information gain)
資訊增益表示得到特徵X的資訊而使得類Y的資訊的不確定性減少的程度。假定離散屬性a有V個可能值
於是可計算出用屬性a對樣本集D進行劃分所獲得的“資訊增益”
一般而言,資訊增益越大,則意味著使用屬性a來劃分所獲得的“純度提升”越大。著名的ID3決策樹學習演算法就是更具資訊增益為準則來選擇劃分屬性的。
由於資訊增益準則對對可取值數目較多的屬性有所偏好,為減少這種偏好可能帶來的不利影響著名的C4.5決策樹演算法不直接使用資訊增益,而是使用“增益率”來選擇最優劃分屬性。
增益率(gain ratio)
其中
“IV(a)”稱為屬性a的“固有值”,屬性a的可能性數目越多(即V越大),則IV(a)的值通常會越大。
需要注意的是,增益率準則對可能取值數目較少的屬性有所偏愛,因此,C4.5演算法並不是直接選擇增益率最大的候選劃分屬性,而是使用了一個啟發式:先從候選劃分屬性中找出資訊增益高於平均水平的屬性,再從中選擇增益率最高的。
資料集
| 編號 | 色澤 | 根蒂 | 敲聲 | 紋理 | 臍部 | 觸感 | 好瓜 |
|---|---|---|---|---|---|---|---|
| 1 | 青綠 | 蜷縮 | 濁響 | 清晰 | 凹陷 | 硬滑 | 是 |
| 2 | 烏黑 | 蜷縮 | 沉悶 | 清晰 | 凹陷 | 硬滑 | 是 |
| 3 | 烏黑 | 蜷縮 | 濁響 | 清晰 | 凹陷 | 硬滑 | 是 |
| 4 | 青綠 | 蜷縮 | 沉悶 | 清晰 | 凹陷 | 硬滑 | 是 |
| 5 | 淺白 | 蜷縮 | 濁響 | 清晰 | 凹陷 | 硬滑 | 是 |
| 6 | 青綠 | 稍蜷 | 濁響 | 清晰 | 稍凹 | 軟粘 | 是 |
| 7 | 烏黑 | 稍蜷 | 濁響 | 清糊 | 稍凹 | 軟粘 | 是 |
| 8 | 烏黑 | 稍蜷 | 濁響 | 清晰 | 稍凹 | 硬滑 | 是 |
| 9 | 烏黑 | 稍蜷 | 沉悶 | 清糊 | 稍凹 | 硬滑 | 否 |
| 10 | 青綠 | 硬挺 | 清脆 | 清晰 | 平坦 | 軟粘 | 否 |
| 11 | 淺白 | 硬挺 | 清脆 | 模糊 | 平坦 | 硬滑 | 否 |
| 12 | 淺白 | 蜷縮 | 濁響 | 模糊 | 平坦 | 軟粘 | 否 |
| 13 | 青綠 | 稍蜷 | 濁響 | 稍糊 | 凹陷 | 硬滑 | 否 |
| 14 | 淺白 | 稍蜷 | 沉悶 | 稍糊 | 凹陷 | 硬滑 | 否 |
| 15 | 烏黑 | 稍蜷 | 濁響 | 清晰 | 稍凹 | 軟粘 | 否 |
| 16 | 淺白 | 蜷縮 | 濁響 | 模糊 | 平坦 | 硬滑 | 否 |
| 17 | 青綠 | 蜷縮 | 沉悶 | 稍糊 | 稍凹 | 硬滑 | 否 |
有興趣的話可以自己算下上面給的公式,這裡直接套用書的算式。
利用該資料預測是不是好瓜,顯然
所以:
ID3演算法
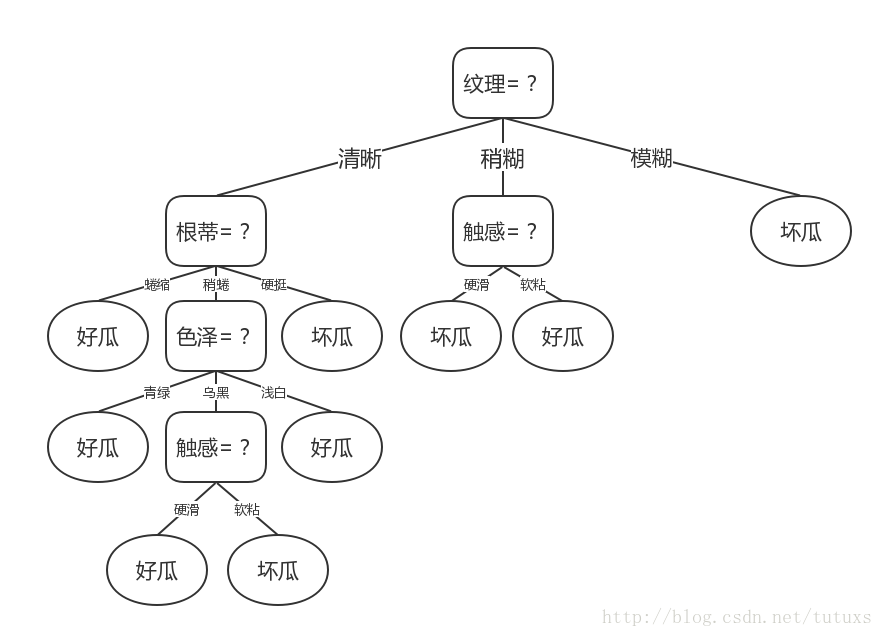
基於資訊增益生成的決策樹圖
虛擬碼:
這裡直接使用了書上的:
輸入:訓練集 D = {(x1, y1), (x2, y2), ... , (xm, ym)}
屬性集 A = {a1, a2, ... , ad}.
過程:函式 TreeGenerate(D, A)
生成結點node;
if D中樣本全屬於同一類別C then
將node標記為C類葉結點; return
end if
if A == ∅ (OR D中樣本在A上取值相同) then
將node標記為葉結點,其類別標記為D中樣本數最多的類; return
end if
從A中選擇最優劃分屬性a*;
for a* 的每一個值 a*_v do
為node生成一個分支;令Dv表示D中在a*上取值為a*_v的樣本子集;
if Dv 為空 then
將分支結點標