線性SVM與SoftMax分類器

1. 線性分類器

在深度學習與計算機視覺系列(2)我們提到了影象識別的問題，同時提出了一種簡單的解決方法——KNN。然後我們也看到了KNN在解決這個問題的時候，雖然實現起來非常簡單，但是有很大的弊端：

分類器必須記住全部的訓練資料(因為要遍歷找近鄰啊！！)，而在任何實際的影象訓練集上，資料量很可能非常大，那麼一次性載入記憶體，不管是速度還是對硬體的要求，都是一個極大的挑戰。
分類的時候要遍歷所有的訓練圖片，這是一個相當相當相當耗時的過程。

這個部分我們介紹一類新的分類器方法，而對其的改進和啟發也能幫助我們自然而然地過渡到深度學習中的卷積神經網。有兩個重要的概念：

得分函式/score function

：將原始資料對映到每個類的打分的函式
損失函式/loss function：用於量化模型預測結果和實際結果之間吻合度的函式

在我們得到損失函式之後，我們就將問題轉化成為一個最優化的問題，目標是得到讓我們的損失函式取值最小的一組引數。

2. 得分函式/score function

首先我們定義一個有原始的圖片畫素值對映到最後類目得分的函式，也就是這裡提到的得分函式。先籠統解釋一下，一會兒我們給個具體的例項來說明。假設我們的訓練資料為xi∈RD，對應的標籤yi，這裡i=1…N表示N個樣本，yi∈1…K表示K類圖片。

比如CIFAR-10資料集中N=50000，而D=32x32x3=3072畫素，K=10，因為這時候我們有10個不同的類別(狗/貓/車…)，我們實際上要定義一個將原始畫素對映到得分上函式 f

:RD↦RK

2.1 線性分類器

我們先丟出一個簡單的線性對映：

f(xi,W,b)=Wxi+b

在這個公式裡，我們假定圖片的畫素都平展為[D x 1]的向量。然後我們有兩個引數：W是[K x D]的矩陣，而向量b為[K x 1]的。在CIFAR-10中，每張圖片平展開得到一個[3072 x 1]的向量，那W就應該是一個[10 x 3072]的矩陣，b為[10 x 1]的向量。

這樣，以我們的線性代數知識，我們知道這個函式，接受3072個數作為輸入，同時輸出10個數作為類目得分。我們把W叫做權重，b叫做偏移向量。

說明幾個點：

我們知道一次矩陣運算，我們就可以藉助W把原始資料對映為10個類別的得分。

其實我們的輸入(xi,yi)其實是固定的，我們現在要做的事情是，我們要調整W, b使得我們的得分結果和實際的類目結果最為吻合。
我們可以想象到，這樣一種分類解決方案的優勢是，一旦我們找到合適的引數，那麼我們最後的模型可以簡化到只有保留W, b即可，而所有原始的訓練資料我們都可以不管了。
識別階段，我們需要做的事情僅僅是一次矩陣乘法和一次加法，這個計算量相對之前…不要小太多好麼…

提前劇透一下，其實卷積神經網做的事情也是類似的，將原始輸入的畫素對映成類目得分，只不過它的中間對映更加複雜，引數更多而已…

2.2 理解線性分類器

我們想想，其實線性分類器在做的事情，是對每個畫素點的三個顏色通道，做計算。咱們擬人化一下，幫助我們理解，可以認為設定的引數/權重不同會影響分類器的『性格』，從而使得分類器對特定位置的顏色會有自己的喜好。

舉個例子，假如說我們的分類器要識別『船隻』，那麼它可能會喜歡圖片的四周都是藍色(通常船隻是在水裡海里吧…)。

我們用一個實際的例子來表示這個得分對映的過程，大概就是下圖這個樣子：

得分函式

原始畫素點向量xi經過W和b對映為對應結果類別的得分f(xi,W,b)=Wxi+b。不過上面這組引數其實給的是不太恰當的，因為我們看到在這組引數下，圖片屬於狗狗的得分最高 -_-||

2.2.1 劃分的第1種理解

圖片被平展開之後，向量維度很高，高維空間比較難想象。我們簡化一下，假如把圖片畫素輸入，看做可以壓縮到二維空間之中的點，那我們想想，分類器實際上在做的事情就如下圖所示：

W中的每一列對應類別中的每一類，而當我們改變W中的值的時候，圖上的線的方向會跟著改變，那麼b呢？對，b是一個偏移量，它表示當我們的直線方向確定以後，我們可以適當平移直線到合適的位置。沒有b會怎麼樣呢，如果直線沒有偏移量，那意味著所有的直線都要通過原點，這種強限制條件下顯然不能保證很好的平面類別分割。

2.2.2 劃分的第2種理解

對W第二種理解方式是，W的每一行可以看做是其中一個類別的模板。而我們輸入圖片相對這個類別的得分，實際上是畫素點和模板匹配度(通過內積運算獲得)，而類目識別實際上就是在匹配影象和所有類別的模板，找到匹配度最高的那個。

是不是感覺和KNN有點類似的意思？是有那麼點相近，但是這裡我們不再比對所有圖片，而是比對類別的模板，這樣比對次數只和類目數K有關係，所以自然計算量要小很多,同時比對的時候用的不再是l1或者l2距離，而是內積計算。

我們提前透露一下CIFAR-10上學習到的模板的樣子：

CIFAR-10模板

你看，和我們設想的很接近，ship類別的周邊有大量的藍色，而car的旁邊是土地的顏色。

2.2.3 關於偏移量的處理

我們先回到如下的公式：

f(xi,W,b)=Wxi+b

公式中有W和b兩個引數，我們知道調節兩個引數總歸比調節一個引數要麻煩，所以我們用一點小技巧，來把他們組合在一起，放到一個引數中。

我們現在要做的運算是矩陣乘法再加偏移量，最常用的合併方法就是，想辦法把b合併成W的一部分。我們仔細看看下面這張圖片：

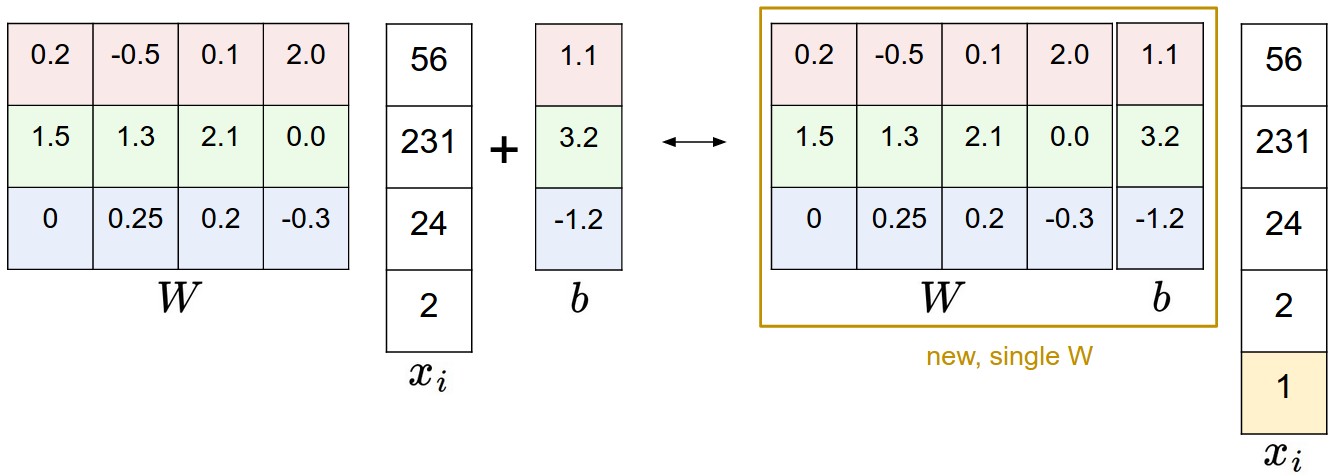
合併W與b

我們給輸入的畫素矩陣加上一個1，從而把b拼接到W裡變成一個變數。依舊拿CIFAR-10舉例，原本是[3072 x 1]的畫素向量，我們添上最後那個1變成[3073 x 1]的向量，而[W]變成[W b]。

2.2.4 關於資料的預處理

插播一段，實際應用中，我們很多時候並不是把原始的畫素矩陣作為輸入，而是會預先做一些處理，比如說，有一個很重要的處理叫做『去均值』，他做的事情是對於訓練集，我們求得所有圖片畫素矩陣的均值，作為中心，然後輸入的圖片先減掉這個均值，再做後續的操作。有時候我們甚至要對圖片的幅度歸一化/scaling。去均值是一個非常重要的步驟，原因我們在後續的梯度下降裡會提到。

2.3 損失函式

我們已經通過引數W，完成了由畫素對映到類目得分的過程。同時，我們知道我們的訓練資料(xi,yi)是給定的，我們可以調整的是引數/權重W，使得這個對映的結果和實際類別是吻合的。

我們回到最上面的圖片中預測 [貓/狗/船] 得分的例子裡，這個圖片中給定的W顯然不是一個合理的值，預測的結果和實際情況有很大的偏差。於是我們現在要想辦法，去把這個偏差表示出來，擬人一點說，就是我們希望我們的模型在訓練的過程中，能夠對輸出的結果計算並知道自己做的好壞。

而能幫助我們完成這件事情的工具叫做『損失函式/loss function』，其實它還有很多其他的名字，比如說，你說不定在其他的地方聽人把它叫做『代價函式/cost function』或者『客觀度/objective』，直觀一點說，就是我們輸出的結果和實際情況偏差很大的時候，損失/代價就會很大。

2.3.1 多類別支援向量機損失/Multiclass Support Vector Machine loss

膩害的大神們定義出了好些損失函式，我們這裡首先要介紹一種極其常用的，叫做多類別支援向量機損失(Multiclass SVM loss)。如果要用一句精簡的話來描述它，就是它(SVM)希望正確的類別結果獲得的得分比不正確的類別，至少要高上一個固定的大小Δ。

我們先解釋一下這句話，一會兒再舉個例子說明一下。對於訓練集中的第i張圖片資料xi，我們的得分函式，在引數W下會計算出一個所有類得分結果f(xi,W)，其中第j類得分我們記作f(xi,W

線性SVM與SoftMax分類器

1. 線性分類器