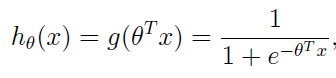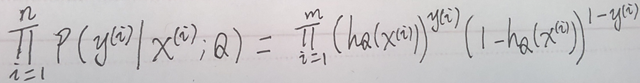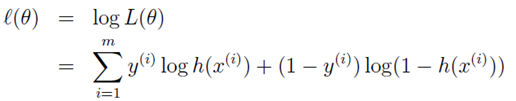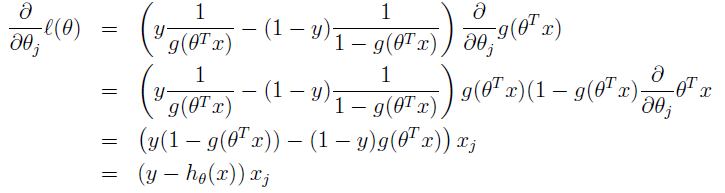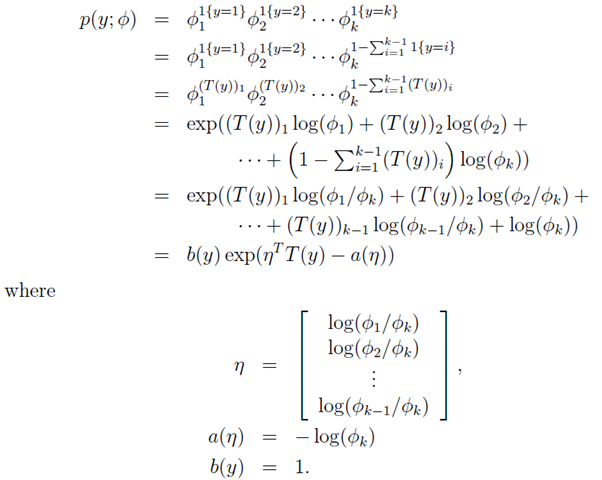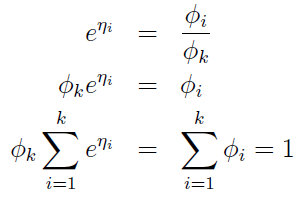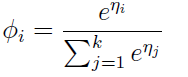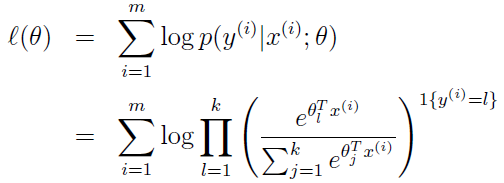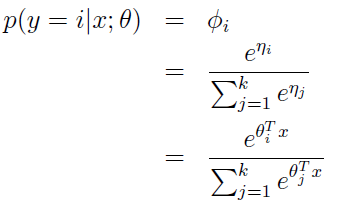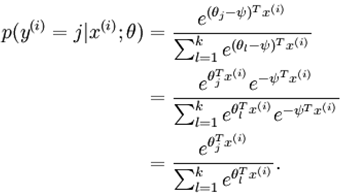Logistic 分類器與 softmax分類器
首先說明啊:logistic分類器是以Bernoulli(伯努利) 分佈為模型建模的,它可以用來分兩種類別;而softmax分類器以多項式分佈(Multinomial Distribution)為模型建模的,它可以分多種互斥的類別。
補充:
什麼是伯努利分佈?伯努利分佈[2] 是一種離散分佈,有兩種可能的結果。1表示成功,出現的概率為p(其中0<p<1)。0表示失敗,出現的概率為q=1-p。
什麼是二項分佈?二項分佈即重複多次的伯努利分佈哦;
什麼是多項式分佈?即它把兩種狀態推廣到了多種狀態,是二項分佈的推廣;
Logistic 分類器
要解決什麼樣的問題呢??假設有一訓練樣本集合X = {x1, x2, x3, ……},其中樣本 xi 由一系列的屬性表示即,xi = (a1, a2, a3,……),並且對於樣本集合X中的樣本要麼屬於類別0, 要麼屬於類別1.
現在呢,我們有一個測試樣本x, 我們根椐上面的知識來推斷: 樣本x 屬於類別0 還是類別1呢??
下面來解決這個問題哦:
1,首先引入引數θ=(θ1,θ2,θ3,……),對於樣本中的屬性進行加權,得到:θTx
2,引入logistic函式(sigmoid函式):g(z) = 1 / (1 + e-z), 該函式常作為神經網路裡的啟用函式的;構建這麼一個式子(待會就會明白它的含義):
logistic函式的影象為:
我們發現呢,它總是介於0-1之間呢,所以呢,我們可以讓 hθ(x) 函式作為一種概率估計哦,如,我們可以讓它表示樣本 x 屬於類別1的概率,即 P(y = 1 | x; θ) = hθ
3. 現在我們有: P(y = 1 | x; θ) = hθ(x) , 與 P(y = 0 | x; θ) = 1 - hθ(x), 那麼呢,我們把它倆聯合起來, 得到:P(y | x; θ) = {hθ(x)}y
4. 現在,我們有了 P(y | x; θ) ,它的含義就是在給定樣本 x 與引數 θ 時,標籤為y 的概率; 然後我們還有一個訓練樣本集合(已經每個樣本的標籤)。現在我們假設每一個訓練樣本是獨立的,我們寫出它們聯合概率密度:
注意:上式中,對應的 y(i) 是已經知道的了哦。其實上式中未知的引數就是 θ 。
其實呢,我們寫的上面的公式就是似然函式啦,我們現在要把它最大化。(什麼意思呢?這裡就要看你對擬然函式的理解了。就是說,隨機事件已經發生了,即把每一個樣本對應的標籤作為隨機事件的話,我們已經知道了它們的具體標籤,我們就就認為已經發生的事件即是概率最大的事件,所以呢,公式中唯一確定的就是引數 θ 了,我們要需要選擇合適的引數θ 使似然函式最大化)
4,最大化似然函式,求出合適的引數θ。
把上面的式子變形為:
然後,我們利用梯度下降法來求引數 θ 。
過程大致是這樣的,先對引數θ的求導,即得到梯度,然後呢,再利用梯度下降法的更新原則來更新引數θ就可以了。
求的梯度(注意哦,引數θ=(θ1,θ2,θ3,……)):
更新法則:
5.現在我們已經得到了參θ了,我們就相當於得到了hθ(x) ,然後呢,我們就可以用它進行對測試樣本進行分類啦。
softmax分類器
它要解決的問題和上面的差不多,唯一的區別就是類別不侷限於兩類,而是多類了。
要解決什麼樣的問題呢??假設有一訓練樣本集合X = {x1, x2, x3, ……},其中樣本 xi 由一系列的屬性表示即,xi = (a1, a2, a3,……),並且對於樣本集合X中的樣本屬於類別C = {c1, c2, c3, ……}中的一種。
現在呢,我們有一個測試樣本x, 我們根椐上面的知識來推斷: 樣本x 屬於哪種類別呢?
現在開始:
首先說一下指數布族,我也沒有花太多的精力放上面哦。
一種形如如下公式的分佈即為指數分佈族:
第二提一下,一個廣義線性模型,其實很多時候,我們很多常見的各種分佈都可以用廣義線性模型來概括。在一個分佈為指數族分佈時,我們如何來定義出一個廣義線性模型呢?作出三個假設:
1,在給定 x 與 引數θ時,y|x 服從以 η 為變數的指數族的分佈:
2, 給定x 時,我們的目標是來預測 T(y)的值。不過在很多時候,T(y) = y;
3, 引數 η =θTx; (為什麼呢? 它就是這麼設計的,廣義線性模型哦)
下面正式推一下softmax迴歸 (可以用它用分類器的哦)
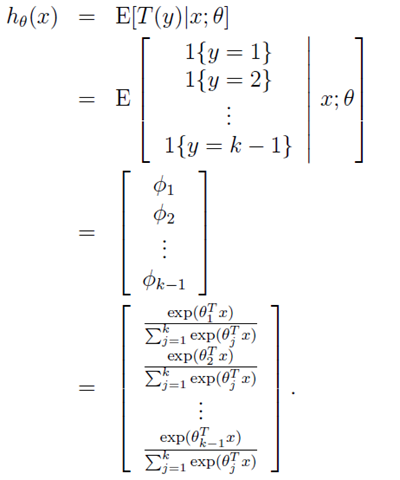
上面已經說了,對於給定的測試樣本 x , 它的輸出 有k種可能 (即可以分為k類),我們分別φ1,φ2,φ3,φ4,……,然後呢,我們定義T(y)如下:
並且定義一個運算 I{真} = 1, I{假} = 0; 所以呢,有:
1,上面的(T(y))i = I{y = i} ,其中(T(y))i 表示T(y)的第i 個元素);
2,E[(T(y))i] = P(y = i) = φi.
下面為推導過程:假設以已經φ的情況,把 p(y; φ)寫出指數分佈族的形式,如下 所示:
注意上面的η是K-1 維的哦,我們現在規定ηk = log(φk/φk) = 0。所以呢, ηi = log(φi / φk),其中i =1,2,……,k)
然後呢,
所以呢,推出:
上面我們假設的φi 已經知道了,其實我們不知道哦,現在我們就推出了怎麼去求φi 了。上面的式子表示了怎麼由ηi去求θi,這就是softmax函式。對於上式的 ηi = θiT x.(應用上面的第三個假設)。 還因為ηk =0,所以呢,我們又規定了θk = 0。(所以,這裡一定注意,θk還是未知數哈,待會用得到這一點)。
其實到這裡基本已經完了,因為我們所關心的φi 已經知道怎麼去求了。
接下來呢,我們來預測T(y)的值哈(看假設的廣義線性模型中的第二點哦)
到這裡就剩下最後一步了,求擬合引數 θ1,θ2,……,θk-1。 可能會問什麼沒有θk呢,因為我們上面規定了θk=0. 追根到底是因為:φk =1-(φ1+φ2+ ……+φk-1).
如何求呢,我們寫出它的似然函式,然後就可以轉變為:用梯主下降或牛頓法等求最值的問題了。它的擬然函式為:
現在呢,我們把引數已經求出來了,可以解決我們的問題了,即給定了一個測試樣本,我們估計它屬於哪一類。方法是我們分別求出對應的φi, 哪個最大,它就屬於哪一類了。
注意:
最後針對這裡我們推出的softmax函式中的公式為:
要說明一點,這裡的未知數的個數為θ1,θ2,……,θk-1, 而 θk = 0,因為我們只需要求出φ1,φ2, ……,φk-1的值來,我們就能求出φk的值。
而在很多用於分類的神經網路中,最後加的softmax的分類器,它是這樣:公式是相同的,但是呢,把θ1,θ2,……,θk-1,θk作為引數,這樣有一個什麼問題呢,那就是過度引數化了(根本用不著這麼多引數嘛),過度引數化會怎樣啊? 假如我們對每一個引數θi 減去一個相同的數,變為θi-ψ,然後呢,
發現了,完全不影響假設函式的預測結果哦。
什麼意思呢???
所以,在現實中,我們需要對代價函式做一個改動:加入權重衰減。權重衰減可以解決 softmax 迴歸的引數冗餘所帶來的數值問題。
.
相關推薦
Logistic 分類器與 softmax分類器
首先說明啊:logistic分類器是以Bernoulli(伯努利) 分佈為模型建模的,它可以用來分兩種類別;而softmax分類器以多項式分佈(Multinomial Distribution)為模型建模的,它可以分多種互斥的類別。 補充: 什麼是伯努利分佈?伯努利分佈[2] 是一種離散分佈,有兩種可能的結
線性SVM與SoftMax分類器
1. 線性分類器 在深度學習與計算機視覺系列(2)我們提到了影象識別的問題,同時提出了一種簡單的解決方法——KNN。然後我們也看到了KNN在解決這個問題的時候,雖然實現起來非常簡單,但是有很大的弊端: 分類器必須記住全部的訓練資料(因為要遍歷找近鄰啊!!),而在任何實際的影象訓練集上,
Head first java chapter 9構造器與垃圾收集器
運算 不同 垃圾 使用 log 特殊 返回 oid div 構造函數是一種特殊的函數。其主要功能是用來在創建對象時初始化對象, 即為v對象成員變量賦初始值,總與new運算符一起使用在創建對象的語句中。構造函數與類名相同,可重載多個不同的構造函數。在JAVA
html class選擇器與id選擇器
spa 寫法 錯誤 一個 html nbsp 元素 -s cnblogs class選擇器: <p class="p1"> .p1{ color:red; ..... } id選擇器: <p id="p2"> #p1{
Css 後代選擇器與子代選擇器的區別
javascrip width 沒有 什麽 for -1 adding 選擇器 light 後代選擇器用空格,比如A B{border:1px solid red;} 子代選擇器用>, 比如A>B{border:1px solid red;} 但是,如果你仔
LVS+keepalived高可用負載均衡集群部署(二)---LAMP網站服務器與LVS服務器
虛擬機l 系統環境: RHEL7 l 硬件環境:虛擬機l 項目描述:為解決網站訪問壓力大的問題,需要搭建高可用、負載均衡的 web集群。 l 架構說明:整個服務架構采用功能分離的方式部署。後端采用2臺mysql 數據庫,實現主從結構以及讀寫分離。中間LAMP網站服務器共有2臺, 前端 2臺LVS服務
【轉】WEB服務器與應用服務器的區別
由於 .net 然而 cluster scala apache servlet 位置 如何使用 https://blog.csdn.net/liupeng900605/article/details/7661406 一.簡述 WEB服務器與應用服務器的區別: 1
爬蟲Scrapy框架-Crawlspider鏈接提取器與規則解析器
一個 htm turn 創建 for tin Coding lines spi 一:Crawlspider簡介 CrawlSpider其實是Spider的一個子類,除了繼承到Spider的特性和功能外,還派生除了其自己獨有的更加強大的特性和功能。其中最顯著的功能就是
CSS的子選擇器與後代選擇器的區別
子選擇器 還有一個比較有用的選擇器子選擇器,即大於符號(>),用於選擇指定標籤元素的第一代子元素。如右側程式碼編輯器中的程式碼: .food>li{border:1px solid red;} 這行程式碼會使class名為food下的子元素li(水果、蔬菜)加入紅色實線邊框。 &
FPGA數字訊號處理(27)卷積編碼器與Viterbi譯碼器設計
卷積編碼與譯碼 訊號在通道間傳輸主要會受到三個方面的影響: 通道本身對訊號產生衰落,這是由於通道本身的頻率響應特性就不理想,對訊號造成破壞; 通道中的各種噪聲,疊加在訊號上改變了訊號的幅度、相位、頻率,造成解調錯誤; 多徑效應,訊號在傳輸過程中的反射、折射、沿
RestFramework之註冊器、響應器與分頁器
一、註冊器的說明與使用 在我們編寫url時經常會因請求方式不同,而重複編寫某條url,而rest_framework中的註冊器幫我節省了很多程式碼 下面介紹一下如何使用 # 利用註冊器來實現路由分發 from rest_framework import routers #
Head first Java 讀書筆記 -----構造器與垃圾收集器
1.棧與堆 1.記憶體中有兩種區域,物件的生存空間--堆(heap),以及方法呼叫和區域性變數的生存空間--棧(stack)。 2.當你呼叫一個方法時,該方法會放在呼叫棧的棧頂。實際被堆上棧的是堆疊塊,堆疊塊帶有方法的狀態,包括執行到哪一行程式以及所有的區域性變數。
CSS中奇數選擇器與偶數選擇器,一句程式碼怎麼實現?
p標籤下的奇數行與偶數行 p:nth-child(odd){} //奇數行 p:nth-child(even){} //偶數行 :nth-child(n) 選擇器匹配屬於其父元素的第 N 個子
CSS 子元素選擇器與後代選擇器區別例項講解
css子元素選擇器和後代選擇器在功能描述上非常相同,但是他們其實是有區別的,本文章通過兩個簡單的例項向大家介紹子元素選擇器與後代選擇器的區別,需要的朋友可以參考一下。 首先我們來了解一下子元素選擇器與後代選擇器的基本語法語法 子元素選擇器的語法如下:div>ul{co
[html5入門-14]一探究竟“後代選擇器與子選擇器的區別”
在學習前端開發時,糾結過後代選擇器和子選擇器的區別,現根據目前所學水平蒐集和整理了這兩種選擇器的區別,分享給大家,如有誤導之處,敬請之處。 一.語法上區別 後代選擇器語法:最高代 下一代 ...子代 代與代之間用空格隔開 子選擇器語法:最高代>下一代>...&g
WEB前端 -- 屬性選擇器與層次選擇器
1.層次選擇器層次選擇器選擇器CSS模式JQuery模式描述後代選擇器ul li a{}$('ul li a')獲取追溯到的多個DOM物件子選擇器div > p{}$('div p')只獲取子類節點的多個DOM物件next選擇器div + p{}$('div + p')
css 當用id選擇器與 class 選擇器選擇同一目標但是應用不同修飾時的選擇問題
為同一個p元素設定id為intro與class為bb,對他們進行不同顏色設定,結果應用了針對id設定時顯示的顏色 <html> <head> <style type="text/css">p{color:red} #intro {colo
巢狀選擇器與子選擇器的不同:
以下程式碼為子選擇器: <!DOCTYPE html PUBLIC "-//W3C//DTD XHTML 1.0 Transitional//EN" "http://www.w3.org/TR/xhtml1/DTD/xhtml1-transitional.dtd">
0016-jQuery選擇器與CSS選擇器
選擇器是jQuery的根基,在jQuery中,對事件處理、遍歷DOM和Ajax操作都依賴選擇器。 CSS選擇器寫法: .demo{ ...//給class為demo的元素新增樣式 } ${".demo"}//給class為demo的元素新增行為 jQuery選擇器的寫法
Spring MVC(攔截器與檢視解析器)
Spring MVC 攔截器: <!--配置攔截器--> <mvc:interceptors> <!--<bean class="com.ma.interceptor.Custom