Andrew Ng機器學習(ML)入門學習筆記(三)
一.分類問題和邏輯迴歸
1.邏輯迴歸的提出
前面舉例較多的房價問題屬於監督學習中的線性迴歸問題,因為需要預測的變數是連續的。對於另一類問題,需要預測的變數是離散的,稱為分類問題。
根據分類種類的多少,又有兩類分類問題和多類分類問題之分。
例如現在有一些腫瘤大小和相應性質(0代表良性,1代表惡性)的訓練資料,如下圖紫色叉點。若仍以線性迴歸進行學習,則可以學習出如下橘色的假設函式
但此時如果多出了一個訓練資料如圖中紅色叉點,仍用線性迴歸就可能訓練出如圖中綠色的
2.邏輯迴歸
對於兩類分類問題,
邏輯迴歸中,
3.假設函式
邏輯迴歸中
4.決策邊界
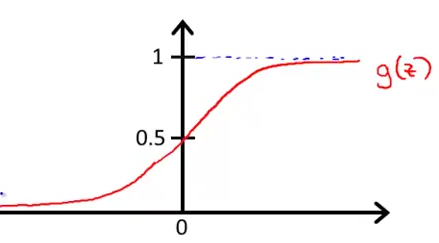
結合假設函式的意義,感覺這是相當合理的預測。再根據S型函式
相關推薦
Vue學習從入門到精通(三)
這一篇文章主要說一下Vue對陣列的各種操作。在說Vue之前,我們先了解一下javascript中對陣列操作的常見函式。 函式 說明 push() 在陣列的末尾新增一個新的元素 pop() 在陣列的末尾刪除掉一個元素
Linux入門實踐筆記(三)——資料盤格式化和和多分割槽掛載
[[email protected] ~]$ sudo fdisk /dev/vdb Welcome to fdisk (util-linux 2.23.2). Changes will remain in memory only, until you decide to write them.
Docker入門實踐筆記(三)一篇文章搞懂Docker下安裝Redis,以及Redis與SpringBoot整合
@Configuration public class RedisConfig { /** * 注入 RedisConnectionFactory */ @Autowired RedisConnectionFactory redisConnectionFacto
Andrew Ng機器學習(ML)入門學習筆記(三)
一.分類問題和邏輯迴歸 1.邏輯迴歸的提出 前面舉例較多的房價問題屬於監督學習中的線性迴歸問題,因為需要預測的變數是連續的。對於另一類問題,需要預測的變數是離散的,稱為分類問題。 根據分類種類的多少,又有兩類分類問題和多類分類問題之分。 例如現在有一些腫
機器學習讀書筆記(三)決策樹基礎篇之從相親說起
方法 事務 家裏 分類 筆記 判斷 都是 rom tro 一、決策樹 決策樹是什麽?決策樹(decision tree)是一種基本的分類與回歸方法。舉個通俗易懂的例子,如下圖所示的流程圖就是一個決策樹,長方形代表判斷模塊(decision block),橢圓形成代
python入門學習筆記(三)——切片、元組
4.操作列表 4.1遍歷整個列表:for name = ['x','y','z'] for x in name: (in後面是可迭代物件‚不要忘記:ƒ迴圈內容要縮排,縮排是靈魂) &
《機器學習實戰》筆記(三):樸素貝葉斯
4.1 基於貝葉斯決策理論的分類方法 樸素貝葉斯是貝葉斯決策理論的一部分,貝葉斯決策理論的的核心思想,即選擇具有最高概率的決策。若p1(x,y)和p2(x,y)分別代表資料點(x,y)屬於類別1,2的概率,則判斷新資料點(x,y)屬於哪一類別的規則是: 4.3 使用條件概率來分類
《自己動手寫java虛擬機器》學習筆記(三)-----搜尋class檔案(go)
專案地址:https://github.com/gongxianshengjiadexiaohuihui 我們都知道,.java檔案編譯後會形成.class檔案,然後class檔案會被載入到虛擬機器中,被我們使用,那麼虛擬機器如何從那裡尋找這些class檔案呢,jav
機器學習筆記(三)Logistic迴歸模型
Logistic迴歸模型 1. 模型簡介: 線性迴歸往往並不能很好地解決分類問題,所以我們引出Logistic迴歸演算法,演算法的輸出值或者說預測值一直介於0和1,雖然演算法的名字有“迴歸”二字,但實際上Logistic迴歸是一種分類演算法(classification y = 0 or 1)。 Log
SQL入門經典(第5版)學習筆記(三)
1.下面這個CREATE TABLE命令能夠正常執行嗎?需要做什麼修改?在不同的資料庫(MySQL、Oracle、SQL Server)中執行,有什麼限制嗎? 不要as: middle_name null 2.能從表裡刪除一個欄位嗎?可以 alter drop coloum?? 3.在前面的表EMP
機器學習筆記(三):線性迴歸大解剖(原理部分)
進入機器學習,線性迴歸自然就是一道開胃菜。雖說簡單,但對於入門來說還是有些難度的。程式碼部分見下一篇,程式碼對於程式設計師還是能能夠幫助理解那些公式的。 (本文用的一些課件來自唐宇迪的機器學習,大家可以取網易雲課堂看他的視訊,很棒) 1.線性迴歸的一些要點 先說
機器學習筆記(三):線性迴歸大解剖(程式碼部分)
這裡,讓我手把手教你如何用邏輯迴歸分析資料 根據學生分數預測是否錄取: #必備3個庫 import numpy as np import pandas as pd import matplotlib.pyplot as plt 讓我們讀入資料: import
機器學習筆記(三) 第三章 線性模型
3.1 基本形式 樣本x由d個屬性描述 x= (x1; x2;…; xd), 線性模型試圖學得一個通過屬性的線性組合來進行預測的函式: 向量形式: w和b學得之後,模型就得以確定. 3.2 線性迴歸 線性迴歸試圖學得 為確定w,b,學習到泛化效能最好的模型
機器學習(西瓜書)學習筆記(三)---------決策樹
1、基本流程 決策樹通常從一個最基本的問題出發,通過這個判定問題來對某個“屬性”進行“測試”,根據測試的結果來決定匯出結論還是匯出進一步的判定問題,當然,這個判定範圍是在上次決策結果的限定範圍之內的。 出發點
機器學習筆記(三):決策樹
決策樹(decision tree)是機器學習中最常見的方法之一,本文主要對決策樹的定義,生成與修剪以及經典的決策樹生成演算法進行簡要介紹。目錄如下 一、什麼是決策樹 二、決策樹的生成 三、決策樹的修剪 四、一些經典的決策樹生成演算法 一、什麼是決策樹 顧名
python3.5《機器學習實戰》學習筆記(三):k近鄰演算法scikit-learn實戰手寫體識別
轉載請註明作者和出處:http://blog.csdn.net/u013829973 系統版本:window 7 (64bit) 我的GitHub:https://github.com/weepon python版本:python 3.5 IDE:Spy
Python3《機器學習實戰》學習筆記(三):決策樹實戰篇之為自己配個隱形眼鏡
轉載請註明作者和出處: http://blog.csdn.net/c406495762 執行平臺: Windows Python版本: Python3.x IDE: Sublime text3 一 前言 上篇文章,Python3《
google機器學習框架tensorflow學習筆記(三)
降低損失:迭代法 迭代學習其實就是一種反饋的結果,有點類似於猜數遊戲,首先你隨便猜一個數,對方告訴你大了還是小了,接著你根據對方提供的資訊進行調整,繼續往正確的方向猜測,如此往復,你通常會越來越接近要猜的數。 這個遊戲真正棘手的地方在於儘可能高效地找到最佳模型。 下圖
機器學習(周志華版)學習筆記(三)歸納偏好
定義:機器學習演算法在學習過程中對某種型別假設的偏好。 每種演算法必有其歸納偏好,否則它將被假設空間中看似在訓練集上“等效”的假設所迷惑,無法產生確定的學習結果。 例子理解: 編號 色澤 根蒂 敲聲 好瓜 1 青綠 蜷縮 濁響 是
Python《機器學習實戰》讀書筆記(四)——樸素貝葉斯
第四章 基於概率論的分類方法:樸素貝葉斯 4-1 基於貝葉斯決策理論的分類方法 優點:在資料較小的情況下仍然有效,可以處理多類別問題 缺點:對於輸入資料的準備方式較為敏感。 適用資料型別:標稱型資料。 假設現在我們有一個數據集,它由兩類資