Logistic迴歸模型

1. 模型簡介：

線性迴歸往往並不能很好地解決分類問題，所以我們引出Logistic迴歸演算法，演算法的輸出值或者說預測值一直介於0和1，雖然演算法的名字有“迴歸”二字，但實際上Logistic迴歸是一種分類演算法（classification y = 0 or 1）。

Logistic迴歸模型：

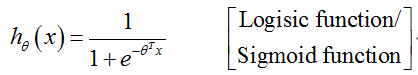
課堂記錄（函式影象）：

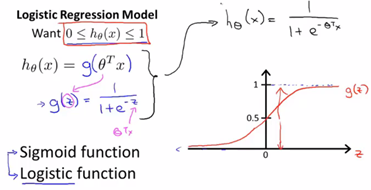
函式h(x)的輸出值，我們把它看做，對於一個輸入值x，y = 1的概率估計。比如說腫瘤分類的例子，我們有一個特徵向量x，似的h(x)的輸出為0.7，我們的假設將這樣解釋：這個具有特徵向量x的患者，患有惡性腫瘤（y=1）的概率為0.7。

進一步理解假設函式：

如上推導過程由y = 0/y = 1，的結論出發，轉化成為對的取值範圍要求。下面引入一個簡單的例子，並介紹決策邊界的概念。

決策邊界：

在上圖例中，我們假設已經擬合出引數，滿足時， ，我們將圖中標為綠色的這條直線稱為決策邊界，這條直線上的點滿足。【注：決策邊界是假設函式的屬性，決定於其引數，不是資料集的屬性。只要給定了假設函式引數，決策邊界（形狀）就確定了。】

在logistic迴歸中，應用更復雜的假設函式，我們就可能得到具有更復雜形狀的決策邊界。

2. 如何擬合Logistic迴歸（假設函式引數）：

具體來說，我要來定義用來擬合引數的代價函式，這便是監督學習問題中Logistic迴歸模型的擬合問題。

我們有一個訓練集，裡面有m個訓練樣本，每個訓練樣本用n+1維的特徵向量表示，特徵。由於是一個分類問題，所以具有這樣的特徵：所有的標籤y不是0就是1。

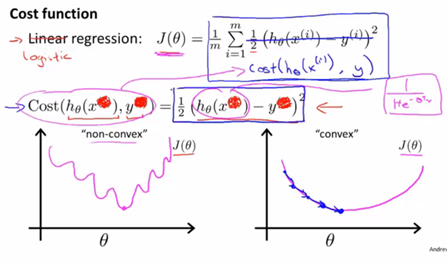
 對於這個代價函式Cost的理解是這樣的，它是在輸出的預測值是時，而實際標籤是y的情況下，我們希望學習演算法付出的代價。由於在Logistic迴歸中我們的假設函式是非線性的，所以我們得到的代價函式可能會是一個非凸函式，如左邊的影象，很顯然如果我們對這樣的使用梯度下降法是無法保證得到全域性最優的。因此我們需要找到一種新的Cost函式形式，使我們得到右側的凸函式影象，以便使用我們比較好的演算法如梯度下降演算法。

凸優化問題：

y = 1的情況

我們對函式的左右兩端（0,1）進行分析可知此代價函式合理（y = 1時，如果，將會獲得巨大的代價；如果，則預測正確，代價為0）。

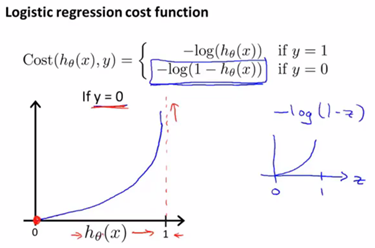
y = 0的情況

同理我們可對其合理性進行分析。

我們可以將代價函式優化後寫成如下更加緊湊的等價形式：

課堂記錄：

Conclusion：

有了代價函式，我們要尋找使其最小的一組引數 。Logistic迴歸整體思路如下：

3. 梯度下降過程：

儘管藍色框中更新引數的規則看起來和線性迴歸的梯度下降引數更新規則基本相同，但實際上由於假設的定義發生變化，它和線性迴歸中的梯度下降實際上是完全不同的。同時，在實現的過程中記得要注意特徵縮放帶來的優化效果。

4. 高階優化：

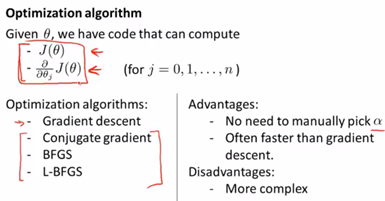
實際上完全有可能成功使用這些演算法並應用於許多不同的學習問題，而不需要真正理解這些演算法的內迴圈在做什麼。同時除非你的研究方向即數值計算，否則都不推薦自己實現這些演算法去應用，因為它們比梯度下降要複雜得多。

下面以一個例子解釋這些高階演算法如何應用。

我們實現一個代價函式costFounction(theta)，它返回兩個引數，其中jVal是我們要計算的代價函式，gradient是一個n*1維向量，其值與偏導數項一一對應。執行這個costFounction函式，完成以上兩部分值的計算後，我們就可以呼叫高階的優化函式，這個函式叫fminunc（in Octave 表示無約束最小化函式）。（首先需要設定一些options：此處設定梯度目標引數為“on”、100次迭代）@costFunction指向我們剛定義的costFunction函式的指標，如果你呼叫它，就會使用高階優化演算法其中的一個，當然你可以把它當做是梯度下降，只不過它能自動選擇學習速率（注：此處使用fminunc時）。

實現程式碼：

有了這些高階優化的概念，並將它們很好的應用於較大規模的機器學習問題。我們就能將Logistic迴歸和線性迴歸模型應用於解決更多的學習問題。

5. 多類別分類問題：

其實我們也可以將二元分類問題的思想用在多分類問題中，稱為一對多的思想。

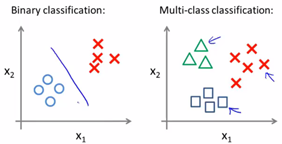
如上圖左側是我們解決二元分類問題的過程。一對多分類的思想如下圖：

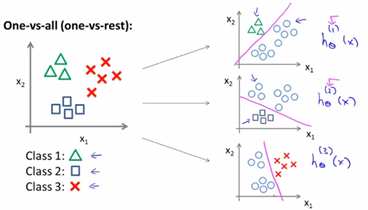
我們擬合出三個分類器，每一個分類器都針對其中一種情況進行訓練，最終我們訓練了邏輯迴歸的分類器，預測i類別y=i的概率。最後為了做出預測，我們對每個分類器輸入一個x，最後取h最大的類別。