Gibbs 取樣完整解析與理解
阿新 • • 發佈:2019-02-08
1.gibbs簡析:
gibbs取樣需要知道樣本中一個屬性在其它所有屬性下的條件概率,然後利用這個條件概率來分佈產生各個屬性的樣本值。gibbs取樣屬於隨機模擬抽樣演算法中的一種(一類近似求解的方法)。隨機模擬的核心是對一個分佈進行抽樣,常用的抽樣演算法包括:1. 接受-拒絕抽樣;2)重要性抽樣;3)MCMC(馬爾科夫鏈蒙特卡洛方法)方法,它包括兩個非常著名的取樣演算法(metropolis-hasting演算法和它的特例Gibbs取樣演算法)(補充:MCMC方法最早由Metropolis(1954)給出,後來Metropolis的演算法由Hastings改進,合稱為M-H演算法。M-H演算法是MCMC的基礎方法。由M-H演算法演化出了許多新的抽樣方法,包括目前在MCMC中最常用的Gibbs抽樣也可以看做M-H演算法的一個特例)。
2.那麼取樣究竟是解決什麼樣的問題?
取樣就是通過將一個不太好解決的問題轉化為一個可以通過取樣來解決的問題,用什麼方法來取樣比較好,這是一個創新的問題,一般沒有固定的解法。
3.常見的取樣方法
3.1 直接取樣(簡單)
3.2 接受-拒絕抽樣(Acceptance-Rejection sampling)下面內容來源
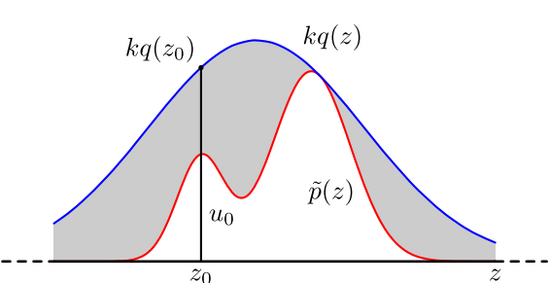
很多實際問題中,p(x)是很難直接取樣的的,因此,我們需要求助其他的手段來取樣。既然 p(x) 太複雜在程式中沒法直接取樣,那麼我設定一個程式可抽樣的分佈 q(x) 比如高斯分佈,然後按照一定的方法拒絕某些樣本,達到接近 p(x) 分佈的目的,其中q(x)叫做 proposal distribution(建議分佈) 。
具體操作如下,設定一個方便抽樣的函式 q(x),以及一個常量 k,使得 p(x) 總在 kq(x) 的下方。(參考上圖)
- 1.x 軸方向:從 q(x) 分佈抽樣得到 a。(如果是高斯,就用之前說過的 tricky and faster 的演算法更快)
- 2 . y 軸方向:從均勻分佈(0, kq(a)) 中抽樣得到 u。
- 3.如果剛好落到灰色區域: u > p(a), 拒絕, 否則接受這次抽樣
- 重複以上過程
在高維的情況下,Rejection Sampling 會出現兩個問題,第一是合適的 q 分佈比較難以找到,第二是很難確定一個合理的 k 值。這兩個問題會導致拒絕率很高,無用計算增加。
4.重要性抽樣(Importance sampling)
重要性取樣的理解是該方法目的並不是用來產生一個樣本的,而是求一個函式的定積分的,只是因為該定積分的求法是通過對另一個叫容易採集分佈的隨機採用得到的。

其中通過對q(x)的隨機取樣,得到大量的樣本x,然後求出f(x)*w(x)的均值,最終得出積分I值。其中的w(x)也就是重要性了,此時如果q(x)概率大,則得到的x樣本數就多,這樣w(x)的值也就多了,也間接體現了它越重要。
5.gibbs 取樣