與簡單線性迴歸相比，多元線性迴歸不過是多了幾個自變數x。

上篇所列的幾個方程更改如下：
多元線性迴歸模型：
y = β0 + β1*x1 + β2*x2 + … + βn*xn + E

多元迴歸方程：
E(y) = β0 + β1*x1 + β2*x2 + … + βn*xn

估計多元迴歸方程：
y_hat = b0 + b1*x1 + b2*x2 + … + bn*xn
利用一個樣本集計算出多元迴歸方程中β0,β1等值的估計值b0,b1等，得到估計方程。

利用樣本計算出方程b0,b1等引數的方法原則依然還是

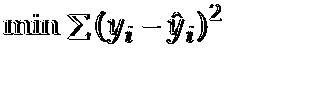
每一組x對應的y值與方程中相應x的y值之差的平方的和最小。
運算與簡單線性迴歸類似，用到線性代數和矩陣代數。這個省略手動的推導計算過程，下面用一個例子以呼叫python中包的方式來實現對引數b0,b1等的求解。

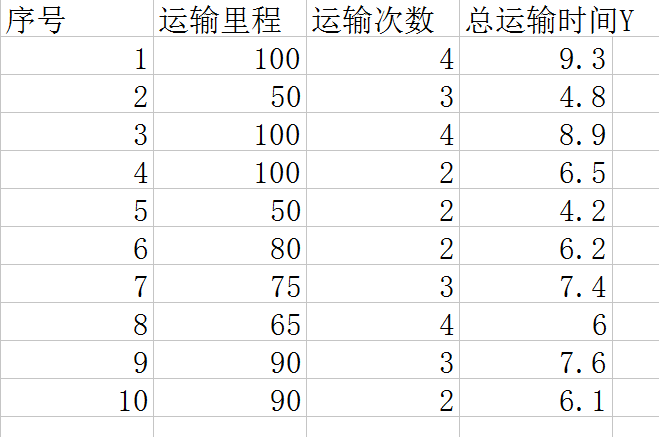
如上圖，有10組資料，分別是一個運送公司關於運輸里程x1,運輸次數x2,以及總運輸時間Y的關係。這是一個自變數數為2的一個多元線性迴歸，我們要根據這些樣本求出估計方程: y估計 = b0 + b1*x1 + b2*x2, 也就是要求出其中的引數b0, b1, b2。為什麼說是估計方程呢？因為樣本只是一部分而不是全體，所以稱其為估計方程。下面利用Python來求解這個問題：

from numpy import genfromtxt
import numpy as np
from sklearn import datasets, linear_model

dataPath = r"C:\Users\zelta\Desktop\Delivery.csv"
 

#加上r就會將後面當做一個完整的字串，而不會認為裡面有什麼轉義之類的。
deliveryData = genfromtxt(dataPath, delimiter = ',')

print "data"
print deliveryData

x = deliveryData[:, :-1]
y = deliveryData[:, -1]

print "x: "
print x
print "y: "
print y

regr = linear_model.LinearRegression()
regr.fit(x, y)

#打印出regr的引數
print "cofficients"
 

print regr.coef_
print "intercept: "
print regr.intercept_

#預測一個例子
xPred = [103, 7]
yPred = regr.predict(xPred)
print "predicted y:"
print yPred
#11.89213978

直接利用sklearn包裡面線性迴歸的函式構造模型，把資料傳入其fit函式中。有一點要注意，提取x,y資料列表的Delivery.csv就是上圖表格資料去除第一行和第一列後的csv檔案。

程式執行結果： 自變數引數分別為 0.0611346 0.92342537， b0為-0.868701466782，取3位小數得到最後的估計方程為：
y_hat = 0.061*x1 + 0.923*x2 - 0.869
利用這個方程就可以根據一組x預測y的值。
我們也可以根據這個方程得到其它的一些資訊，比如平均運送距離每增加1公里，運輸時間增加0.0611小時，平均每多運輸1次，運輸時間增加0.923小時。

還有一個問題，當自變數x中有分型別的變數該如何解決呢？比如x中有一個變數是車型: 3種車， 自行車，電瓶車，汽車。這也會影響最後的運輸時間，給這3種車編個號0，1，2。表格變成如下圖。

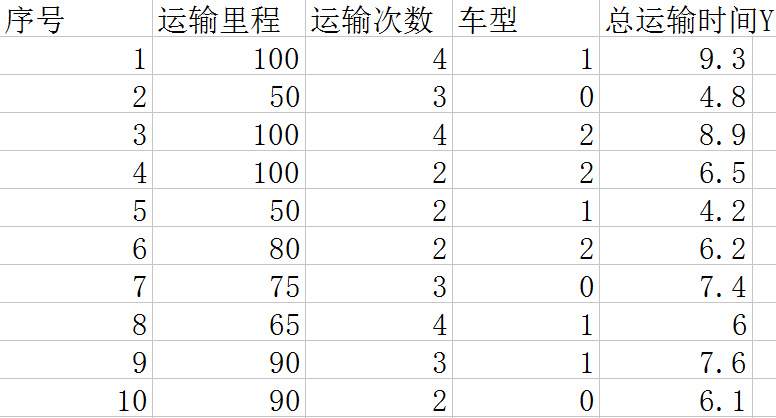
這個時候我們不能利用車型的值作為x進行運算，因為車型的值只是表示類別，沒有大小關係。這裡要用到前面幾篇中利用到的方法，將其轉化為數字型的資料進行運算。也就是如下圖：

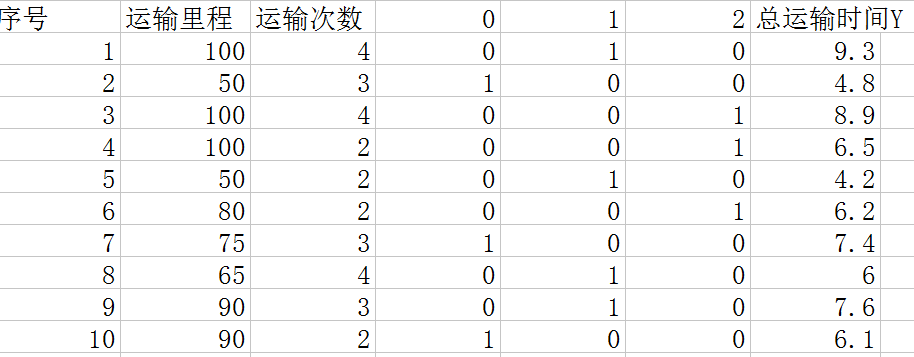
用3個x變數來表示車型。這樣就可以把型別的變數轉化為資料型的變數代入方程進行運算。