Matlab 實現顯著性檢測模型效能評價演算法之AUC
阿新 • • 發佈:2019-02-10
AUC預備知識:
1. 常用來評價一個二分類器的優劣。
2. 很多學習器是為測試樣本產生一個實值或概率預測,然後這個預測值與一個分類閾值進行比較,若大於閾值則為正類,否則為反類。
3. 實際上,根據這個實值或概率預測結果,可以將測試樣本進行排序,"最可能"(實值或概率預測最大)是正例的排在最前面,“最不可能”是正例的排在最後面。這個,分類過程就相當於在這個排序中以某個“截斷點”(即閾值)將樣本分為兩部分,前面為正,後面為反。
4. TP: 真正例,真實為正例,預測也為正例;
FP: 假正例,真實為負例,預測為正例;
TPR: 真正例率,真正例數 / 總真實的正例數;
FPR: 假正例率,假正例數 / 總真實的負例數。
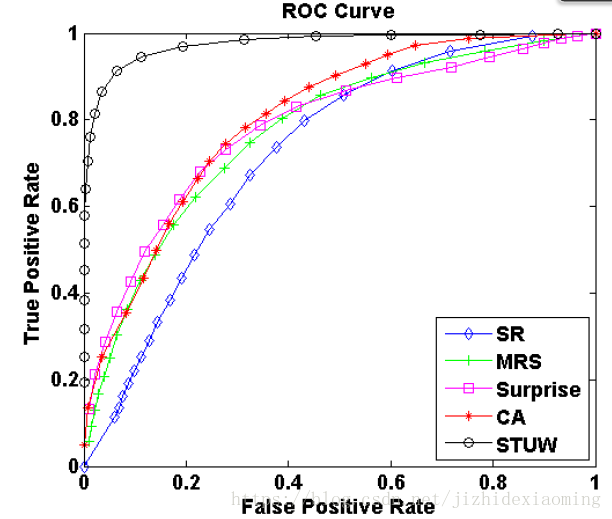
在顯著性檢測領域,生成的顯著圖的每個畫素即為一個樣本,顯著圖的畫素按從大到小排序,然後從第一個(畫素值最大)依次作為閾值,對所有畫素進行分類,然後求得一組TPR, FPR。再以第二大的畫素值為閾值,又可以得到一組。以FPR為橫軸,以TPR為縱軸,即可得到ROC曲線,如下,ROC曲線的面積值即為AUC (area under curve)
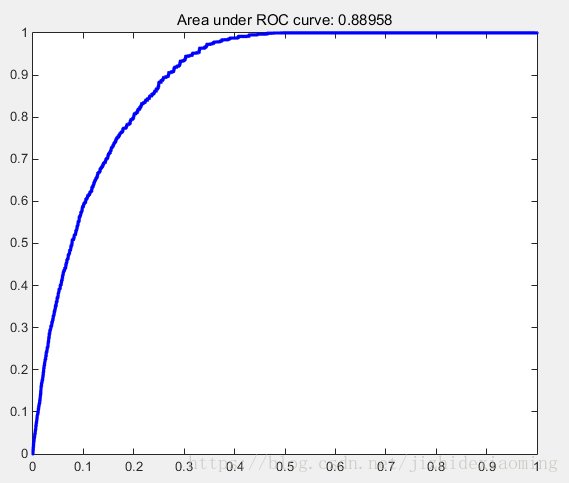
1,Matlab實現,算出auc = 0.8895,利用gongAUC_Judd.m,算出的auc = 0.8872
clear; clc; smap_full_path = strcat('D:\Code\Matlab\Map\smap.jpg'); gmap_full_path = strcat('D:\Code\Matlab\Map\gmap.jpg'); smap = imread(smap_full_path); gmap = imread(gmap_full_path); gmap = imresize(gmap,size(smap)); smap = imresize(smap,0.1); gmap = imresize(gmap,0.1); % 二值化ground truth map, 只要兩類 thresh_value = graythresh(gmap); final_gmap = im2bw(gmap, thresh_value); % smap歸一化到[0,1] smap = mat2gray(smap); % % [score,tp,fp,allthreshes] = AUC_Judd(smap, final_gmap, 1, 1); % 陣列 smap_array = smap(:); gmap_array = final_gmap(:); % 總真實為正例數 idex = find(gmap_array == 1); P_num = length(idex); % 總真實為負例數 N_num = length(gmap_array) - P_num; % 從大到小排序,orig_location儲存了排序前畫素在smap_array的位置 [saliency_values, orig_location] = sort(smap_array, 'descend'); % TP(1) = 0; FP(1) = 0; % TP(end) = 1; FP(end) = 1; % 當以salicy_values(i)為閾值時,前面陣列saliency_values前面i個都判為正例 for i=1:length(saliency_values) % 檢視前i個被判為正例的畫素,真實情況如何。 TP(i) = 0; % 真正例,真實為正例,預測也為正例; FP(i) = 0; % 假正例,真實為負例,預測為正例; for m=1:i if gmap_array(orig_location(m)) == 1 TP(i) = TP(i) + 1; else FP(i) = FP(i) + 1; end end FPR(i) = FP(i) / N_num; TPR(i) = TP(i) / P_num; end auc = trapz(FPR,TPR); % 以FPR為x軸,以TPR為y軸,算積分,即為ROC下的面積 plot(FPR, TPR, '.b-'); title(['Area under ROC curve: ', num2str(auc)])
2, AUC_Judd.m
% created: Tilke Judd, Oct 2009 % updated: Zoya Bylinskii, Aug 2014 % This measures how well the saliencyMap of an image predicts the ground % truth human fixations on the image. % ROC curve created by sweeping through threshold values % determined by range of saliency map values at fixation locations; % true positive (tp) rate correspond to the ratio of saliency map values above % threshold at fixation locations to the total number of fixation locations % false positive (fp) rate correspond to the ratio of saliency map values above % threshold at all other locations to the total number of posible other % locations (non-fixated image pixels) function [score,tp,fp,allthreshes] = AUC_Judd(saliencyMap, fixationMap, jitter, toPlot) % saliencyMap is the saliency map % fixationMap is the human fixation map (binary matrix) % jitter = 1 will add tiny non-zero random constant to all map locations % to ensure ROC can be calculated robustly (to avoid uniform region) % if toPlot=1, displays ROC curve if nargin < 4, toPlot = 0; end if nargin < 3, jitter = 1; end score = nan; % If there are no fixations to predict, return NaN if ~any(fixationMap) disp('no fixationMap'); return end if any(saliencyMap(:)) saliencyMap = saliencyMap/sum(saliencyMap(:)); end if any(fixationMap(:)) fixationMap = fixationMap/sum(fixationMap(:)); end % % make the saliencyMap the size of the image of fixationMap % if size(saliencyMap, 1)~=size(fixationMap, 1) || size(saliencyMap, 2)~=size(fixationMap, 2) % saliencyMap = imresize(saliencyMap, size(fixationMap)); % end % jitter saliency maps that come from saliency models that have a lot of % zero values. If the saliency map is made with a Gaussian then it does % not need to be jittered as the values are varied and there is not a large % patch of the same value. In fact jittering breaks the ordering % in the small values! % if jitter % % jitter the saliency map slightly to distrupt ties of the same numbers % saliencyMap = saliencyMap+rand(size(saliencyMap))/10000000; % end % % normalize saliency map % saliencyMap = (saliencyMap-min(saliencyMap(:)))/(max(saliencyMap(:))-min(saliencyMap(:))); % % if sum(isnan(saliencyMap(:)))==length(saliencyMap(:)) % disp('NaN saliencyMap'); % return % end S = saliencyMap(:); F = fixationMap(:); Sth = S(F>0); % sal map values at fixation locations Nfixations = length(Sth); Npixels = length(S); allthreshes = sort(Sth, 'descend'); % sort sal map values, to sweep through values tp = zeros(Nfixations+2,1); fp = zeros(Nfixations+2,1); tp(1)=0; tp(end) = 1; fp(1)=0; fp(end) = 1; for i = 1:Nfixations thresh = allthreshes(i); aboveth = sum(S >= thresh); % total number of sal map values above threshold tp(i+1) = i / Nfixations; % ratio sal map values at fixation locations above threshold fp(i+1) = (aboveth-i) / (Npixels - Nfixations); % ratio other sal map values above threshold end score = trapz(fp,tp); allthreshes = [1;allthreshes;0]; if toPlot % subplot(121); imshow(saliencyMap, []); title('SaliencyMap with fixations to be predicted'); % hold on; % [y, x] = find(fixationMap); % plot(x, y, '.r'); % subplot(122); plot(fp, tp, '.b-'); title(['Area under ROC curve: ', num2str(score)]) end