相信學習程式設計的同學，或多或少都接觸到演算法的時間複雜度和空間複雜度了，那我來講講怎麼計算。

       常用的演算法的時間複雜度和空間複雜度 一，求解演算法的時間複雜度，其具體步驟是：

　　⑴ 找出演算法中的基本語句；

　　演算法中執行次數最多的那條語句就是基本語句，通常是最內層迴圈的迴圈體。

　　⑵ 計算基本語句的執行次數的數量級；

　　只需計算基本語句執行次數的數量級，這就意味著只要保證基本語句執行次數的函式中的最高次冪正確即可，可以忽略所有低次冪和最高次冪的係數。這樣能夠簡化演算法分析，並且使注意力集中在最重要的一點上：增長率。

　　⑶ 用大O記號表示演算法的時間效能。

　　將基本語句執行次數的數量級放入大O記號中。

　　如果演算法中包含巢狀的迴圈，則基本語句通常是最內層的迴圈體，如果演算法中包含並列的迴圈，則將並列迴圈的時間複雜度相加。例如：

　　for (i=1; i<=n; i++)　　x++;

　　for (i=1; i<=n; i++)　　for (j=1; j<=n; j++)　　x++;

　　第一個for迴圈的時間複雜度為O(n)，第二個for迴圈的時間複雜度為O(n2)，則整個演算法的時間複雜度為O(n+n2)=O(n2)。

　　常見的演算法時間複雜度由小到大依次為：

　　O(1)＜O(log2n)＜O(n)＜O

Ο(1)表示基本語句的執行次數是一個常數，一般來說，只要演算法中不存在迴圈語句，其時間複雜度就是O(1)。O(log2n)、O(n)、O(nlog2n)、O(n2)和O(n3)稱為多項式時間，而O(2n)和O(n!)稱為指數時間。電腦科學家普遍認為前者是有效演算法，把這類問題稱為P（Polynomial,多項式）類問題，而把後者稱為NP（Non-Deterministic Polynomial,非確定多項式）問題。

在計算演算法時間複雜度時有以下幾個簡單的程式分析法則: 
   (1).對於一些簡單的輸入輸出語句或賦值語句,近似認為需要O(1)時間 
   (2).對於順序結構,需要依次執行一系列語句所用的時間可採用大O下"求和法則" 求和法則:是指若演算法的2個部分時間複雜度分別為 T1(n)=O(f(n))和 T2(n)=O(g(n)),則 T1(n)+T2(n)=O(max(f(n),g(n)))。特別地,若T1(m)=O(f(m)), T2(n)=O(g(n)),則 T1(m)+T2(n)=O(f(m)+g(n)) 
   (3).對於選擇結構,如if語句,它的主要時間耗費是在執行then字句或else字句所用的時間,需注意的是檢驗條件也需要O(1)時間 
   (4).對於迴圈結構,迴圈語句的執行時間主要體現在多次迭代中執行迴圈體以及檢驗迴圈條件的時間耗費,一般可用大O下"乘法法則" 
乘法法則: 是指若演算法的2個部分時間複雜度分別為 T1(n)=O(f(n))和 T2(n)=O(g(n)),則 T1*T2=O(f(n)*g(n)) 
   (5).對於複雜的演算法,可以將它分成幾個容易估算的部分,然後利用求和法則和乘法法則技術整個演算法的時間複雜度 
   另外還有以下2個運演算法則:(1) 若g(n)=O(f(n)),則O(f(n))+O(g(n))=O(f(n))；(2)O(Cf(n)) = O(f(n)),其中C是一個正常數。

幾個常見的時間複雜度進行示例說明：

(1)、O(1) 

 Temp=i; i=j; j=temp;                     
   以上三條單個語句的頻度均為1，該程式段的執行時間是一個與問題規模n無關的常數。演算法的時間複雜度為常數階，記作T(n)=O(1)。注意：如果演算法的執行時間不隨著問題規模n的增加而增長，即使演算法中有上千條語句，其執行時間也不過是一個較大的常數。此類演算法的時間複雜度是O(1)。 

（2)、O(n2)

交換i和j的內容

1.sum=0；（一次）   

2.for(i=1;i<=n;i++) （n+1次）   

3.for(j=1;j<=n;j++)（n（n+1）次）   

4.sum++；（n（n+1）+1次） 

因為(2n2+n+1)=n2（即：去低階項，去掉常數項，去掉高階項的常參得到），所以T(n)= =O(n2)；

一般情況下，對步進迴圈語句只需考慮迴圈體中語句的執行次數，忽略該語句中步長加1、終值判別、控制轉移等成分，當有若干個迴圈語句時，演算法的時間複雜度是由巢狀層數最多的迴圈語句中最內層語句的頻度f(n)決定的。

(3)、O(n)  

1.a=0;   

2.b=1;               ①   

3.for (i=1;i<=n;i++) ②   

4.{s=a+b;            ③   

6.b=a;               ④     

7.a=s; }             ⑤

語句1的頻度為2,語句2的頻度為n,語句3的頻度為n-1,語句4的頻度為n-1,語句5的頻度為n-1, 即T(n)=2+n+3(n-1)=4n-1=O(n). 

(4)、O(log2n) 

1. i=1;   ①   

2. while (i<=n)   

3. i=i*2; ② 

語句1的頻度是1,設語句2的頻度是f(n),則：2^f(n)<=n;f(n)<=log2n，取最大值f(n)=log2n,即T(n)=O(log2n) 

(5)、O(n3)  

1. for(i=0;i<n;i++){     

2. for(j=0;j<i;j++){   

3.for(k=0;k<j;k++)   

4.x=x+2; }}

當i=m,j=k的時候,內層迴圈的次數為k當i=m時, j可以取 0,1,...,m-1 ,所以這裡最內迴圈共進行了0+1+...+m-1=(m-1)m/2次所以,i從0取到n,則迴圈共進行了:0+(1-1)*1/2+...+(n-1)n/2=n(n+1)(n-1)/6所以時間複雜度為O(n3).

二，演算法的空間複雜度：

類似於時間複雜度的討論，一個演算法的空間複雜度(Space Complexity)S(n)定義為該演算法所耗費的儲存空間，它也是問題規模n的函式。漸近空間複雜度也常常簡稱為空間複雜度。 空間複雜度(Space Complexity)是對一個演算法在執行過程中臨時佔用儲存空間大小的量度。一個演算法在計算機儲存器上所佔用的儲存空間，包括儲存演算法本身所佔用的儲存空間，演算法的輸入輸出資料所佔用的儲存空間和演算法在執行過程中臨時佔用的儲存空間這三個方面。演算法的輸入輸出資料所佔用的儲存空間是由要解決的問題決定的，是通過引數表由呼叫函式傳遞而來的，它不隨本演算法的不同而改變。儲存演算法本身所佔用的儲存空間與演算法書寫的長短成正比，要壓縮這方面的儲存空間，就必須編寫出較短的演算法。演算法在執行過程中臨時佔用的儲存空間隨演算法的不同而異，有的演算法只需要佔用少量的臨時工作單元，而且不隨問題規模的大小而改變，我們稱這種演算法是“就地\"進行的，是節省儲存的演算法，如這一節介紹過的幾個演算法都是如此；有的演算法需要佔用的臨時工作單元數與解決問題的規模n有關，它隨著n的增大而增大，當n較大時，將佔用較多的儲存單元。

當一個演算法的空間複雜度為一個常量，即不隨被處理資料量n的大小而改變時，可表示為O(1)；當一個演算法的空間複雜度與以2為底的n的對數成正比時，可表示為0(10g2n)；當一個演算法的空間複雜度與n成線性比例關係時，可表示為0(n).若形參為陣列，則只需要為它分配一個儲存由實參傳送來的一個地址指標的空間，即一個機器字長空間；若形參為引用方式，則也只需要為其分配儲存一個地址的空間，用它來儲存對應實參變數的地址，以便由系統自動引用實參變數。

演算法的空間複雜度通過計算演算法所需的儲存空間實現，演算法空間複雜度的計算公式記作：S(n)= O(f(n))，其中，n為問題的規模，f(n)為語句關於n所佔儲存空間的函式。

一般情況下，一個程式在機器上執行時，除了需要儲存程式本身的指令、常數、變數和輸入資料外，還需要儲存對資料操作的儲存單元。若輸入資料所佔空間只取決於問題本身，和演算法無關，這樣只需要分析該演算法在實現時所需的輔助單元即可。若演算法執行時所需的輔助空間相對於輸入資料量而言是個常數，則稱此演算法為原地工作，空間複雜度為O(1)。關於O(1)的問題， O(1)是說資料規模和臨時變數數目無關，並不是說僅僅定義一個臨時變數。舉例：無論資料規模多大，我都定義100個變數，這就叫做資料規模和臨時變數數目無關。就是說空間複雜度是O(1)。

對於一個演算法，其時間複雜度和空間複雜度往往是相互影響的。當追求一個較好的時間複雜度時，可能會使空間複雜度的效能變差，即可能導致佔用較多的儲存空間；反之，求一個較好的空間複雜度時，可能會使時間複雜度的效能變差，即可能導致佔用較長的執行時間。另外，演算法的所有效能之間都存在著或多或少的相互影響。因此，當設計一個演算法(特別是大型演算法)時，要綜合考慮演算法的各項效能，演算法的使用頻率，演算法處理的資料量的大小，演算法描述語言的特性，演算法執行的機器系統環境等各方面因素，才能夠設計出比較好的演算法。

常用的演算法的時間複雜度和空間複雜度

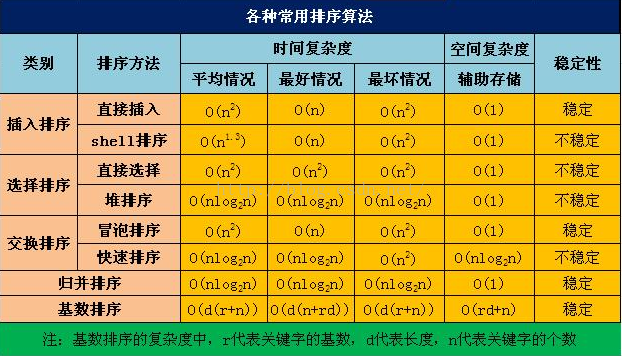
一個經驗規則：其中c是一個常量，如果一個演算法的複雜度為c 、 log2n 、n 、 n*log2n ,那麼這個演算法時間效率比較高 ，如果是2n ,3n ,n!，那麼稍微大一些的n就會令這個演算法不能動了，居於中間的幾個則差強人意。 
       演算法複雜度分析是一個很重要的問題，任何一個程式設計師都應該熟練掌握其概念和基本方法，而且要善於從數學層面上探尋其本質，才能準確理解其內涵。