關聯規則R語言實戰(Apriori演算法)
最近遇到一個業務問題需要用關聯規則的演算法來實現,為了解決業務問題,我又重新複習了一遍以前就學過的Apriori演算法並將其運用到業務場景中。下面,我想談一談在在具體的業務實現過程中我的一些感想。
一.理論背景
1.1基本術語定義
X和Y各代表某一個項集,M代表樣本中的總項集數。
1.2關聯規則的三個度量
衡量關聯規則有三個最基本也是最重要的指標,我將其稱為‘三度’。這裡的三度指的可不是《三傻大鬧寶萊塢》裡面那三個蠢萌蠢萌的印度人,而是指的度量關聯規則最基礎也是最核心的指標三兄弟:支援度,置信度,提升度。
下面我將對這三兄弟進行逐一介紹。
老大支援度,是‘三度’家族裡最沉穩最老實的孩子。出於兄長對兩個弟弟的謙讓之情,關聯規則家族建立的時候,老大主動表示他要來度量關聯規則中最苦最累隨時要給弟弟們提供理論支援的概念。關聯規則家族表示老大good job,於是便給老大賜名為支援度,基本公式是
老二置信度,是‘三度’家族中最高調也是最不折手段的孩子。為了獲得最重要的地位,老二踩著老大的肩膀往上爬,於是,他獲得了賜名:置信度,基本公式是
老三提升度,是‘三度’家族中容易被人給遺忘的小可憐。從定義上來說,老三算是老大支援度和老二置信度的結合體,可由於老二置信度太醒目了,許多人在做關聯規則時在沒有完全吃透理論的情況下往往容易忽略老三提升度的存在。下面先給出老三提升度的公式
1.3Apriori演算法理論
在瞭解了關聯規則的三個度的基本定義之後,下一步則需要闡述清楚Apriori演算法的基本定義。
在講Apripri演算法之前,我們首先要清楚兩個概念:
1)設定最小支援度的閾值,如果一個項集的支援度大於等於最小支援度,則其為頻繁項集,如果一個項集的支援度小於最小支援度,則其為非頻繁項集。
2)對於一個項集,如果它是頻繁集,則它的子集均是頻繁集;如果它是非頻繁集,則它的父集都是非頻繁集。這是因為一個項集的所有子集的支援度都大於等於它本身,一個項集的所有父親的支援度都小於等於它本身。
有了上面兩個概念打底,Apriori演算法就可以被定義了。Apripri演算法主要分為三步:
1)設定最小支援度的閾值。從單項集開始,先計算所有單項集的支援度,過濾掉非頻繁單項集及其父集;將剩餘的單項集組合為二項集,先計算所有二項集的支援度,過濾掉非頻繁二項集及其父集;不斷地迭代上述過程,最後篩選出所有的頻繁項集。
2)設定最小置信度的閾值。對頻繁項集進行計算,求出滿足置信度條件的強關聯規則。
3)設定最小提升度的閾值。對第2)步進行計算,求出滿足提升度條件的強關聯規則,作為最後的關聯規則的模型結果。
相比於最原始的一一計算,使用Apripor演算法計算頻繁項集可以大大地減少運算量,提升計算效率。
到底,理論的梳理就完全結束,下一步我將會對關聯規則進行實戰演練。
二.實操演練
2.1資料來源
因為業務需要保密,所以實戰演練部分我並沒有用業務中的真實資料來進行記錄,而是借用了arules包中和我業務資料很像的Epub資料來對我的建模過程來進行一個回顧和梳理。
Epub資料包含了來自維也納大學經濟與工商管理學院的電子文件平臺的下載歷史。
library(arules)
#匯入資料
>data(Epub)
#檢視資料型別
>class(Epub)
[1]"transactions"
#因為我的業務資料是從oracle資料庫裡面匯出來的,所以我這裡便把Epub資料轉成data.frame格式,然後匯出到資料庫之後,重新從資料庫匯入,以便能夠記錄整個建模流程
>Epub<-as(Epub,"data.frame")
#因為業務不需要,所以演示時也去掉時間欄位
>Epub<-Epub[,1:2] 匯出進資料庫因為不屬於建模流程,這裡就不記錄了。
2.2資料準備
上一節對資料來源進行了基本的闡釋下面正式進入正題,我將會從資料庫匯入開始一步步記錄我的建模流程。
首先,是資料準備過程。
#引入連結資料庫的RODBC包
library(RODBC)
#連線資料庫
channel<-odbcConnect("資料庫名",uid="orcl",pwd="orcl")
#讀入資料
Epub<-sqlQuery(channel,"select * from Epub")
#檢視資料前六行
head(Epub)此時資料應該是如下表格的data.frame結構:
| transactionID | items |
|---|---|
| session_4795 | doc_154 |
| session_4797 | doc_3d6 |
| session_479a | doc_16f |
| session_47b7 | session_47b7 |
| session_47b7 | session_47b7 |
| session_47b7 | doc_f4 |
這個時候,表格是資料庫儲存的格式而非事務集的格式,因此首先要對資料進行格式轉換。
首先,要對資料進行分組,一個transactionID的所有items應該在一個組裡,因此,我們可以使用split函式,指定它的分組變數和目標變數:
>Epub<-split(Epub$items,Epub$transacionID)
#分組之後,將Epub資料轉換成事務集形式
>Epub<-as(Epub,"transacions")
#檢視Epub資料的前十行
>inspect(Epub[1:10])
items transactionID
[1] {doc_154} session_4795
[2] {doc_3d6} session_4797
[3] {doc_16f} session_479a
[4] {doc_11d,doc_1a7,doc_f4} session_47b7
[5] {doc_83} session_47bb
[6] {doc_11d} session_47c2
[7] {doc_368} session_47cb
[8] {doc_11d,doc_192} session_47d8
[9] {doc_364} session_47e2
[10] {doc_ec} session_47e7 Eupb已經被轉化成了事務集,到此,我們就已經做好資料的準備。
2.3建模
資料準備好之後,就進入整個流程中最重要也是最核心的建模步驟中了。
#檢視資料集統計彙總資訊
>summary(Epub)
transactions as itemMatrix in sparse format with
15729 rows (elements/itemsets/transactions) and
936 columns (items) and a density of 0.001758755
most frequent items:
doc_11d doc_813 doc_4c6 doc_955 doc_698 (Other)
356 329 288 282 245 24393
element (itemset/transaction) length distribution:
sizes
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19
11615 2189 854 409 198 121 93 50 42 34 26 12 10 10 6 8 6 5 8
20 21 22 23 24 25 26 27 28 30 34 36 38 41 43 52 58
2 2 3 2 3 4 5 1 1 1 2 1 2 1 1 1 1
Min. 1st Qu. Median Mean 3rd Qu. Max.
1.000 1.000 1.000 1.646 2.000 58.000
includes extended item information - examples:
labels
1 doc_11d
2 doc_13d
3 doc_14c
includes extended transaction information - examples:
transactionID
10792 session_4795
10793 session_4797
10794 session_479a
#可以使用dim函式提取項集數和item數
>dim(Epub)
[1] 15729 936 第一步,檢視資料集的統計彙總資訊。summary()含義的具體解釋如下:
1)共有15729個項集和936 個item,稀疏矩陣中1的百分比為0.001758755。
2)most frequent items描述了最頻繁出現的5個item以及其分別出現的次數。
3)sizes描述了項集的項的個數以及n項集共有幾個,例如單項集有10個,二項集有11個,58項集有1個。sizes之後描述了sizes對應的5個分位數和均值的統計資訊。
#統計每個item的支援度
>itemFreq<-itemFrequency(Epub)
#每個項集transaction包含item的個數
>Size<-size(Epub)
#每個item出現的次數
> itemCount<-(itemFreq/sum(itemFreq)*sum(Size))除此之外,還可以更直觀地作圖觀測itemFrequency。
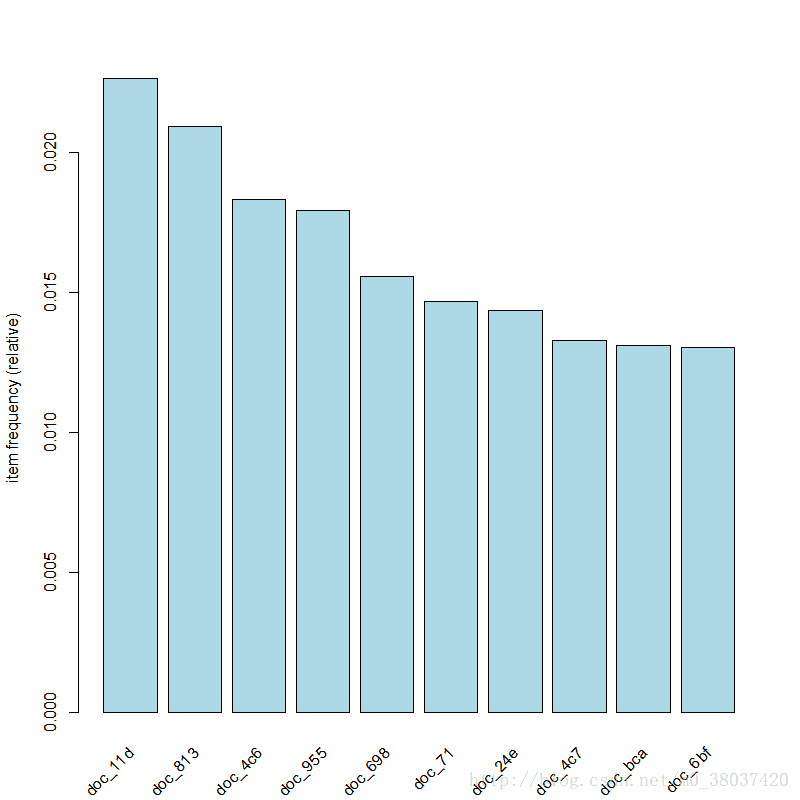
#檢視支援度排行前10的圖
>itemFrequencyPlot(Epub,topN=10,col="lightblue")當對資料的基本統計資訊心中有數之後,就開始最重要的建模步驟。
#最小支援度0.001,最小置信度0.6,最小項數2
>rules<-apriori(Epub,parameter=list(support=0.001,confidence=0.6,minlen=2)) 這裡解釋一下最小項數。minlen和maxlen表示LHS+RHS並集的元素的最小個數和最大個數。有意義的規則起碼是LHS和RHS各至少包含1個元素,所以minlen為2。
生成模型之後,觀測模型結果。
#展示生成的規則
inspect(sort(rules,by="lift"))
lhs rhs support confidence lift
[1] {doc_6e7,doc_6e8} => {doc_6e9} 0.001080806 0.8095238 454.7500
[2] {doc_6e7,doc_6e9} => {doc_6e8} 0.001080806 0.8500000 417.8016
[3] {doc_6e8,doc_6e9} => {doc_6e7} 0.001080806 0.8947368 402.0947
[4] {doc_6e9} => {doc_6e8} 0.001207960 0.6785714 333.5391
[5] {doc_6e9} => {doc_6e7} 0.001271537 0.7142857 321.0000
[6] {doc_506} => {doc_507} 0.001207960 0.6551724 303.0943
[7] {doc_6e8} => {doc_6e7} 0.001335113 0.6562500 294.9187
[8] {doc_6e7} => {doc_6e8} 0.001335113 0.6000000 294.9187
[9] {doc_87c} => {doc_882} 0.001335113 0.6000000 171.5891 將會具體的展示生成的每一條強規則,其對應的支援度support,置信度confidence ,提升度。
可以指定搜尋條件,檢視規則的子集。