推薦演算法-關聯規則|R

阿新 • • 發佈：2018-12-30

推薦演算法-關聯規則

1 概念

關聯規則是常見的推薦演算法，從發現大量使用者行為資料中發現有強關聯的規則。

關聯規則是一種無監督的機器學習方法，用於知識發現。

優點是能夠從大量行為資料中挖掘出無法直接感受到的規則，往往能給出意想不到的規則組合。缺點是難以進行模型評估，一般通過行業經驗判斷結果是否合理。
關聯規則最經典的是購物籃分析，啤酒和尿布就是一個經典案例。運用在早期亞馬遜、京東、淘寶等購物推薦場景中，往往表現為”買過這本書的人還買了XXX”,”看了這部電影的人還想看XXX”。其推薦結果包含的個性化資訊較低，相對簡單粗暴。（別人都買的我就買哦，我不要面子的啊！）

2 常用演算法

關聯規則中最常用的演算法是Apriori，此外還有FP-Growth,Eclat

2.1 基本概念

假設存在規則{A，B}->{C}，則稱：

{A,B}為前項，記為LHS(Left Hand Side)

{C}為後項，記為RHS(Right Hand Side)

支援度
支援度的計算物件為項集，上例中，{A,B},{C}均為項集。項集支援度，即項集在所有交易中出現的交易數。support(A)=n(A)/N
置信度(confidence)
置信度的物件是規則，{A}->{B}為一條規則，以該規則為例，其置信度為AB同時出現的次數佔B出現的次數比例，即confidence(A->B)=N(AB)/N(B)

提升度(lift)
規則的提升度在於說明項集{A}和項集{B}之間的獨立性，Lift=1說明{A}和{B}相互獨立，說明兩個條件沒有任何關聯。如果Lift<1,說明兩個事件是互斥的。一般認為Lift>3才是有價值的規則。可以這樣理解規則的提升度：將兩種物品捆綁銷售的結果，比分別銷售兩種物品的結果提升的倍數。support和confidence都很高的時候，不代表規則很好，通常很可能是Lift很高。計算公式如下：
Lift(A−>B)=support(AB)support(A)support(B)
頻繁項集
支援度大於一定閾值的規則成為頻繁項集，這個閾值通常由經驗給出，或者通過對資料探索得到。

強關聯規則
置信度大於一定閾值的頻繁項集為強關聯規則，閾值通常也是通過經驗給出，或通過資料探索得到，可通過不斷的嘗試和調整確定合適的閾值。

2.2 Apriori演算法

Apriori思想的精髓:如果一個項集不是頻繁項集，那麼它的所有父集都不是頻繁項集;一個項集是頻繁項集，那麼它的子集必然是頻繁項集。

2.2.1 演算法步驟

Step1：產生頻繁項集
1.1找出所有僅包含1個專案的項集，計算支援度
1.2篩選留下滿足最小支援度的項集
1.3擴充套件項集個數，步長為1個，計算項集支援度
1.4 重複1.2
1.5重複以上步驟，至沒有可擴充套件項集，得到頻繁項集
Step2:產生關聯規則
1.1 獲取Step1所有規則的置信度
1.2對比置信度閾值，超過閾值的即為強關聯規則
2.2.2 例項解析
原資料如下：

id	Items
001	{A,B,C}
002	{B,C,D}
003	{C,E}
004	{D}
005	{A}

首先計算最少個數項集的支援度

Item	Support
{A}	0.4
{B}	0.4
{C}	0.6
{D}	0.4
{E}	0.2

設定Min(Support)=0.3,則項集E被剔除，此後也不再考慮包含{E}的任何組合了。
拓展項集長度，得到如下結果：

Item	Support
{A,B}	0.2
{A,C}	0.2
{B,C}	0.4
{B,D}	0.2
{C,D}	0.2

MIn(Support)=0.3,則剩下{B,C}組合，由於繼續拓展只有{B,C,D}，而{B,D}和{C,D}組合已經被捨棄。因此不再拓展。

Conf(B,C)=22∗3
若其置信度不滿足要求，則認為該資料集中沒有發現強關聯規則。

2.3 FP-Growth演算法

補充

2.4 Eclat演算法

補充

3 Apriori案例

（1）安裝並載入相關的包：

install.packages("arules");library(arules) #規則生成
install.packages("arulesViz");library(arulesViz) #資料視覺化
install.packages("RColorBrewer");library(RColorBrewer)  #繪圖

（2）載入資料
arules包可以讀取兩種格式的資料
A.同一個交易的商品在同一行，以某種分隔符分隔（實際資料檔案中不含ID列）

ID	Itemset
1	A,B,C
2	B,C

讀取語句

data=read.transactions("F:/data.txt",format="basket",sep=",")

B.以ID標識，一個商品一行

ID	Item
1	A
1	B
1	C
2	B
2	C

讀取語句

data<-read.transactions("F:/data/data.txt",format="single",cols=c("id","item"),sep=",") #cols是必須的

本文案例使用的資料是arules包自帶的交易資料集Groceries

data(Groceries) #獲取資料

瞭解資料情況可以使用以下程式碼：

summary(Groceries) #資料概況
inspect(Groceries)[1:6,] #列印資料前6行，注意，head()在這裡不能列印資料

這裡寫圖片描述
輸出結果可以看到資料集有多少交易記錄，涵蓋了多少種商品；購買次數最多的是哪些商品；單筆交易購買的商品個數分佈；資料標籤（這裡label是關聯規則中的item,level1,level2是商品標籤）。
使用arules包可以簡單計算出關聯規則結果，也可以通過基礎變數的計算得到關聯規則。

(3)頻繁項集生成
A.基於概念計算

itemsize<-size(Groceries)#得到唯一id內購買的item個數
itemF<-itemFrequency(Groceries)#得到每個item的支援度
itemCnt<-(itemF/sum(itemF))/sum(itemsize)#得到item出現次數
itemFrequencyPlot(Groceries,suppory=0.1) #按照支援度直觀觀測item分佈

上述計算僅能簡單計算和觀測單個item的支援度，通過apriori函式能夠根據閾值得到關聯規則

B.使用apriori函式

rules<-apriori(Groceries,parameter=list(supp=0.006,conf=0.25,minlen=2))

引數解讀:
apriori(data,parameter,appearance,control):
*data是經過處理，讀取為transactions的資料
*parameter指定為一個list,可設定引數包括,其中，support設定了最小支援度閾值，confidence設定了最小置信度閾值，minlen表示LHS+RHS的最小專案個數，maxlen則是最多個數,target=“rules”為預設值。
注意：minlen=1代表−>A這樣的規則成立，因此一般設置minlen=2
詳細用法使用help(apriori)可得

rules結果，可以看到滿足條件的規則數，supp、conf、lift分佈,項集個數分佈等資訊

> summary(rules)
set of 463 rules

rule length distribution (lhs + rhs):sizes
  2   3   4 
150 297  16 

   Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
  2.000   2.000   3.000   2.711   3.000   4.000 

summary of quality measures:
    support           confidence          lift       
 Min.   :0.006101   Min.   :0.2500   Min.   :0.9932  
 1st Qu.:0.007117   1st Qu.:0.2971   1st Qu.:1.6229  
 Median :0.008744   Median :0.3554   Median :1.9332  
 Mean   :0.011539   Mean   :0.3786   Mean   :2.0351  
 3rd Qu.:0.012303   3rd Qu.:0.4495   3rd Qu.:2.3565  
 Max.   :0.074835   Max.   :0.6600   Max.   :3.9565  

mining info:
      data ntransactions support confidence
 Groceries          9835   0.006       0.25

(4)規則結果探索

檢視規則、排序

inspect(s_rules[1:6])#檢視具體的規則
s_rules<-sort(rules,by="lift") #依據lift排序
s_rules<-sort(rules,by="support")  #依據support排序
s_rules<-sort(rules,by="confidence") #依據confidence排序

注意，rules是S4類型，不能夠實用head()查看

實際運用中，通常是有針對性、直接的的需求，比如想看一些物品有沒有存在有關的關聯規則，或者某些物品直接是否存在關聯，可以通過對rules進行篩選

sample<-subset(rules,item %in% c("fuiit"))
sample<-subset(rules,item %in% c("fuiit") & lift>3)

%in% :精確匹配 item %in% c(“a”,”b”)表示，item=”a” or item =”b”
%pin%: 部分匹配 item %pin% c(“a”,”b”)表示，item like “a” or item like “b”
%ain%:完全匹配:item %ain% c(“a”,”b”)表示，item =”a” and item = “b”
同時可以使用條件運算子(&,|,!)對support、confidence、lift進行過濾

使用subset篩選規則，是同時對LHS和RHS進行檢索，如需要針對LHS或RHS篩選，可使用下列語句

> rules_log=subset(rules,lhs %in% "yogurt") #針對LHS篩選，得到的是邏輯變數
> rules_log=subset(rules,rhs %in% "yogurt") #針對RHS篩選

(5)規則視覺化
根據支援度、置信度、提升度檢視資料分佈，可直觀感知生成規則的分佈，可調整閾值

##需載入擴充套件包arulesViz
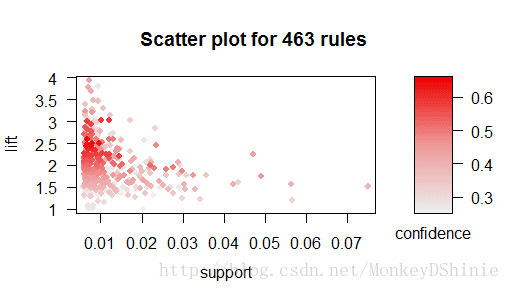
plot(rules) #直接繪製散點圖，預設conf、supp為縱軸橫軸，lift為顏色深淺
plot(rules,measure=c("support","lift"),shading="conf")#個性化設定

引數解讀
*measure 標出了橫軸和縱軸基於的變數
*shading代表點的顏色深淺基於的變數

這裡寫圖片描述

從散點圖看，得到的規則聚集在support<0.015,置信度處於(0.45-0.55)，lift處於(1.8,2.3)的區域上。受lift極值和support極值的影響，規則的散點分佈並不十分明顯，可以僅聚集部分規則的散點圖

#通過subset篩選規則
plot(subset(rules,support<0.02 & lift<3),measure=c("support","lift"),shading="conf")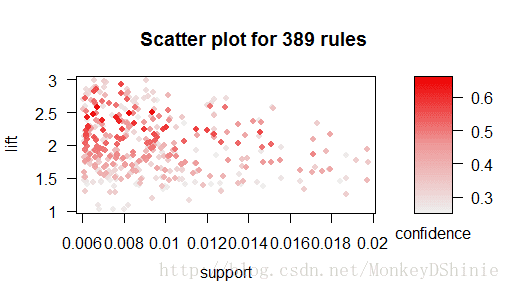

這裡寫圖片描述

篩選了support<0.02其lift<3的規則，並使用散點圖展示

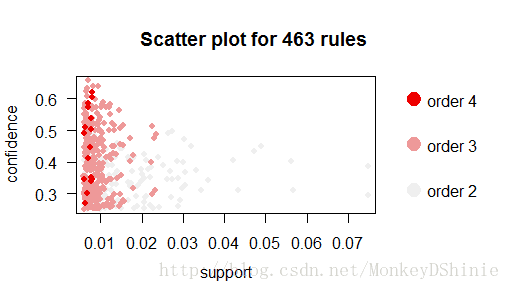
plot(rules, shading = "order") #顏色使用項集個數區分

這裡寫圖片描述

其他視覺化形式還有：

#基於分組矩陣，對規則進行聚類
plot(rules, method = "grouped")

這裡寫圖片描述
個人認為，可理解性較差，不便解讀，修改method引數（arulesViz.plot），可以得到更多展現方式。

4 FP-Growth案例

待補充

5 Eclat案例

待補充

By Shinie

推薦演算法-關聯規則|R