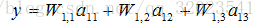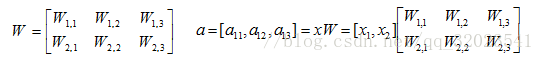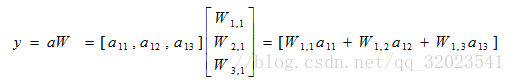基本概念：計算圖，張量，會話

計算圖是相互運算不影響的兩個計算模型，是定義計算的執行，且互不影響

#在TensorFlow程式中，系統會自動維護一個預設的計算圖，也支援通過tf.Graph 生成新的計算圖
#不同計算圖上的張量和運算都不會共享
import tensorflow as tf
print(a.graph is tf.get_default_graph()) #獲取預設的計算圖
g1 = tf.Graph()
with g1.as_default():
    #在計算圖 g1 中定義變數"v"，並設定初始值為 0
    v = tf.get_variable("v",initializer = tf.zeros_initializer(shape = [1]))
g2 = tf.Grahp()
with g2.as_default():
    #在計算圖 g2 中定義變數"v",並設定初始值為 1
    v = tf.ger_variable("v",initializer = tf.ones_initializer(shape = [1]))

#在計算圖 g1 中讀取變數 "v" 的值
with tf.Session(graph = g1) as sess:
    tf.initialize_all_variables().run()  #初始化變數
    with tf.variable_scope("layer1",reuse = True): #變數空間後續會介紹
        print(sess.run(tf.get_variable("v"))) #輸出為 0 
#在計算圖 g2 中讀取變數 "v" 的值
with tf.Session(graph = g2) as sess:
    tf.initialize_all_variables().run()
    with tf.variable_scope("layer1",reuse = True):
        print(sess.run(tf.get_variable("v"))) #輸出為 1
        print(v.eval()) #可以通過 節點.eval(session=xxx) 獲取計算值
 

張量 Tensor 從名字上就能看出是一個基本的概念，在TensorFlow中所有的資料都通過張量的形式來表示。從功能的角度看，張量可以被簡單理解為多維資料。其中0階張量就是標量，表示一個數，第 n 階張量就是 n 維的陣列。但是張量在TensorFlow中並不是直接採用陣列的形式實現，它只是對TensorFlow中運算結果的引用，在張量中並沒有真正儲存數字。

import tensorflow as tf
#tf.constant 是一個計算，這個計算的結果為一個張量，儲存在變數 a 中
a = tf.constant([1.0,2.0],name = "a")
b = tf.constant([2.0,3.0],name = "b")
result = tf.add(a,b,name = "add")
print result
"""
輸出：
Tensor("add:0",shape = (2,),dtypt=float32)
"""
 

從上面的程式碼的執行結果可以看出，一個張量中主要儲存了三個屬性：name，shape，type

shape=(2,) 表示張量 result 是一個一維陣列，這個陣列的長度為 2

會話是TensorFlow用來執行計算的模型，會話擁有並管理TensorFlow程式執行時的所有資源。當所有計算完成後需要關閉會話來幫助系統回收資源。

#建立一個會話
sess = tf.Session()
#執行計算
sess.run(...)
#關閉會話來釋放資源
sess.close()

#也可以用python中的上下文管理器來管理會話的開啟和關閉
with tf.Session() as sess:
    sess.run(...)
#不需要呼叫 sess.close() 來關閉了
 

TensorFlow實現神經網路

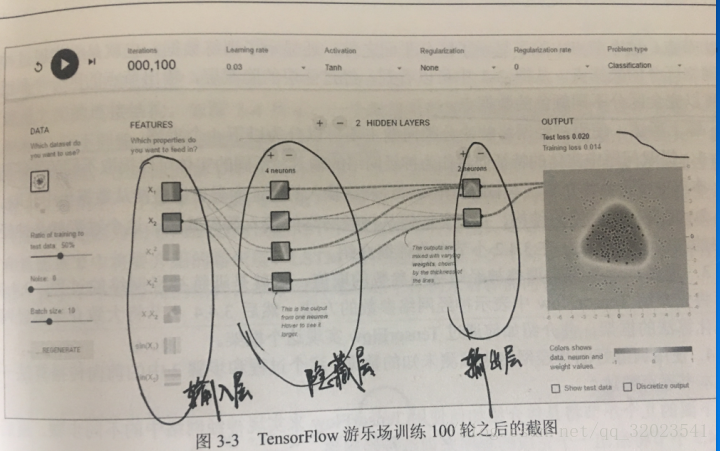
如圖是一個包含三層的簡單神經網路，輸入層 x1 和 x2 ，隱藏層有 4 個節點，輸出層有兩個節點，如果把(x1,x2)當做某一個笛卡爾座標系的取值，而點的顏色代表x1,x2這個節點的輸出值。使用神經網路解決分類問題就可以分為以下4個步驟
1）提取問題中實體的特徵向量作為神經網路的輸入
2）定義神經網路的結構，並定義如何從神經網路的輸入得到輸出
3）通過訓練資料來調整神經網路中引數的取值，這就是訓練神經網路的過程

4）使用訓練好的神經網路來預測未知的資料

這麼說吧，假設有一些產品，知道一些合格品的長度和質量，也知道一些不合格品的長度和質量，上圖的x1 和 x2就可以分別代表長度和質量引數，結果可以用數字 y 來代表合格與不合格。如果用上圖的網路來實現，那麼我們已經走到了第二步，即神經網路的結構已經定義好了，現在開始的是訓練過程，而訓練一個神經網路，需要解析它的前向傳播演算法。

前向傳播演算法簡介

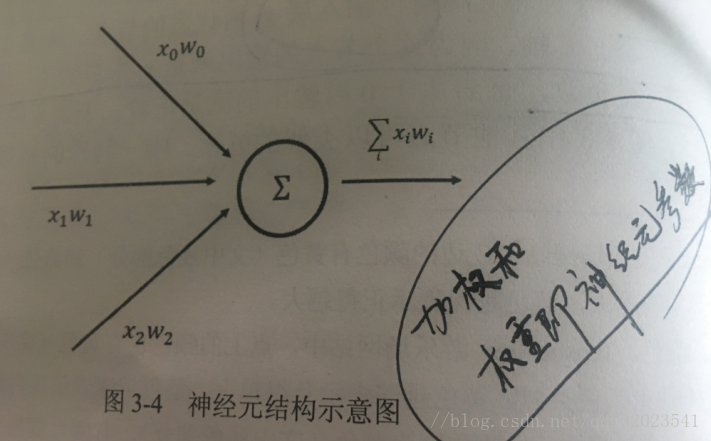
這裡介紹最簡單的全連線網路結構的前向傳播演算法，為了展示全連線網路結構，我們先了解神經元的傳播。

從圖可以看出，一個神經元有多個輸入和一個輸出。一個最簡單的神經元結構的輸出就是所有輸入的加權和，而不同輸入的權重就是神經元的引數。這個引數的調節就是神經網路的訓練過程。

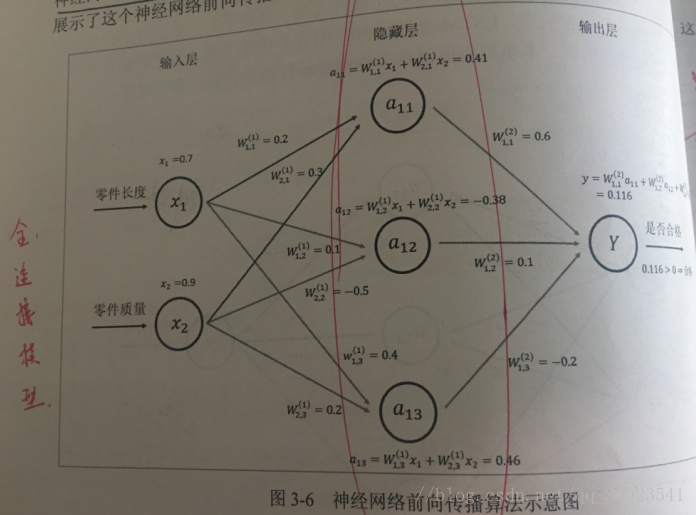
現在我們回到前面定義的神經網路，這個網路的資料傳播過程如下，每條線代表神經元的一個連線，每條線上的權重用W表示，為了簡化，我們將隱藏層減為 3 個節點。

如圖所示，給出了x1,x2從輸入層一層一層前向傳播的演算法過程。

將輸入 x1,x2組織成一個 1*2 的矩陣 x = [x1,x2]，W組成一個2*3的矩陣

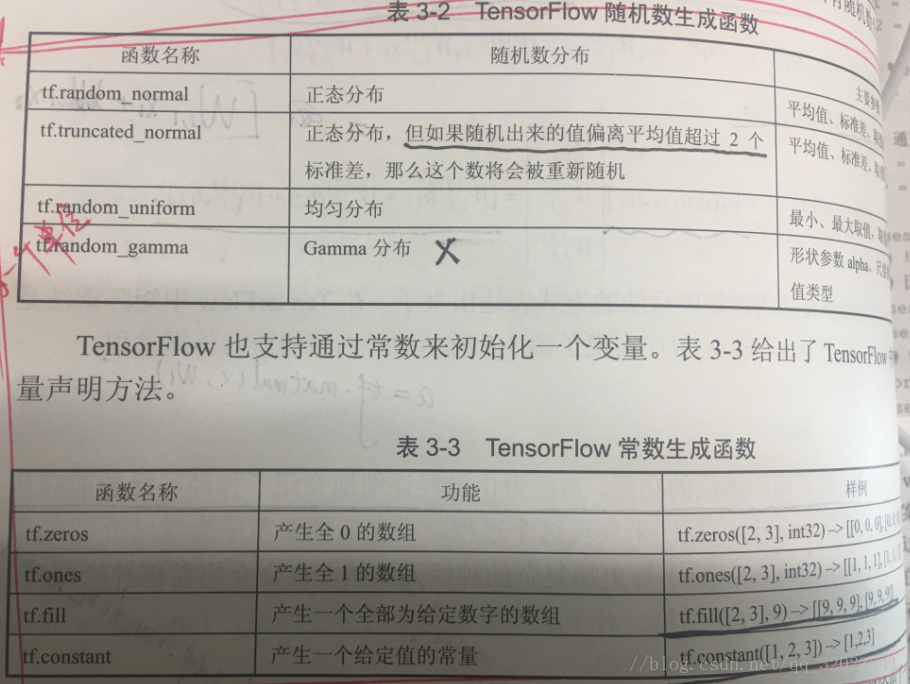
TensorFlow變數函式如下

用程式碼表示上述前向傳播公式如下

import tensorflow as tf
#宣告 w1,w2 兩個變數，這裡還通過 seed 引數設定了隨機種子
#這樣可以確保每次執行得到的結果是一樣的
w1 = tf.Variable(tf.random_normal([2,3],stddev = 1,seed =1))
w2 = tf.Variable(tf.random_normal([3,1],stddev = 1,seed =1))

#暫時將輸入的特徵向量定義為一個常量，注意這裡 x 是一個 1*2 的矩陣
x = tf.constant([[0.7,0.9]])

#前向傳播演算法
a = tf.matmul(x,w1)
y = tf.matmul(a,w2)

sess = tf.Session()
init_op = tf.initialize_all_variables()
sess.run(init_op)
print(sess.run(y))
sess.close()