%設一被控物件G（s）=50/(0.125s^2+7s),
%用增量式PID控制演算法編寫模擬程式
%（輸入分別為單位階躍、正弦訊號，取樣時間為1ms，控制器輸出限幅：[-5,5],
%  模擬曲線包括系統輸出及誤差曲線，並加上註釋、圖例）。

clear all;
close all; 
ts=0.001;                 %取樣時間
sys=tf(50,[0.125,7, 0]); %tf是傳遞函式  即被控物件函式G（）;
dsys=c2d(sys,ts,'z');    %把控制函式離散化
[num,den]=tfdata(dsys,'v');% 離散化後提取分子、分母  
u_1=0.0;
u_2=0.0;
y_1=0.0;
y_2=0.0;
x=[0,0,0]';
error_1=0;
error_2=0;
for k=1:1:1000
time(k)=k*ts;                        %取樣次數
S=2;
if S==1
    kp=10;ki=0.1;kd=15;             %初始化PID  
    rin(k)=1;                       %Step Signal 
elseif S==2
    kp=10;ki=0.1;kd=15;             
    rin(k)=0.5*sin(2*pi*k*ts);       %Sine Signal     即實際輸入    
end 
du(k)=kp*x(1)+kd*x(2)+ki*x(3);      %PID Controller   控制係數  
u(k)=u_1+du(k);                     %Restricting the output of controller
if u(k)>=5       
   u(k)=5;
end
if u(k)<=-5
   u(k)=-5;
end
%Linear model
yout(k)=-den(2)*y_1-den(3)*y_2+num(2)*u_1+num(3)*u_2;          %實際輸出
error(k)=rin(k)-yout(k);                                       %Return of parameters 誤差
u_2=u_1;                                                       %儲存上上次輸入   為下次計算
u_1=u(k);                                                      %儲存上一次控制係數   為下次計算
y_2=y_1;                                                       %儲存上上次次輸出   為下次計算
y_1=yout(k);                                                   %儲存上一次輸出   為下次計算
x(1)=error(k)-error_1;                                         %Calculating P
x(2)=error(k)-2*error_1+error_2;                               %Calculating D
x(3)=error(k);                                                 %Calculating I 
error_2=error_1;                    
error_1=error(k);                    
end
figure(1);
plot(time,rin,'b',time,yout,'r');                        %輸入 和實際控制輸出
xlabel('time(s)'),ylabel('rin,yout'); 
figure(2);
plot(time,error,'r')                                     %輸入與輸出誤差輸出曲線
xlabel('time(s)');ylabel('error');
 

3.1 建立數學建模

　　設被控物件等效傳遞函式為

3.2 模擬建模(略)

3.3 模擬實驗

　　在傳統的PID 調節器中，引數的整定問題是控制面臨的最主要的問題，控制系統的關鍵之處便是將Kp、Ti、Td三個引數的值最終確定下來。而在工業過程控制中首先需要對PID 控制中三參量對系統動態性的影響進行實際深入地瞭解，才能確定怎樣將三引數調節到最佳狀態。在本實驗中，對各參量單獨變化對系統控制作用的影響進行討論，其中在對一個參量變化引發的影響進行討論時，需要將其餘兩個引數設定為常數。

　　3.3.1 P 控制作用分析

　　分析比例控制作用。設Td= 0、Ti=∞、Kp= 3 ~ 10.輸人訊號階躍函式，分別進行模擬，如圖3 所展示的系統的階躍響應曲線。

　　圖3 顯示的模擬結果表明：系統的超調量會隨著Kp值的增大而加大，系統響應速度也會會隨Kp值的增大而加快。但是系統的穩定效能會隨著Kp的增大而變差。

　　圖3 單閉環調速系統P控制階躍響應曲線

　　3.3.2 比例積分控制作用的分析

　　設比例積分調節器中Kp= 1,討論Ti= 0.01 ~ 0.05 時。輸人訊號階躍函式，分別進行模擬，如圖4 所展示的系統的系統的階躍響應曲線。

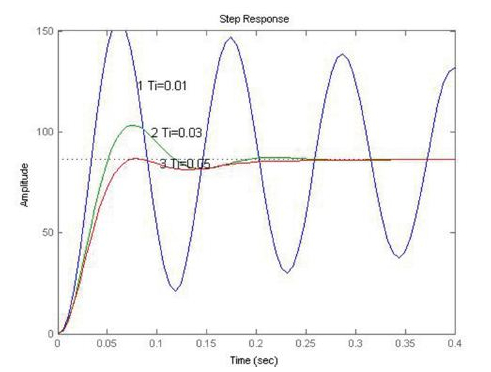
　　圖4 單閉環調速系統PI控制階躍給定響應曲線

　　系統的超調量會隨著Ti值的加大而減小，系統響應速度隨著Ti值的加大會略微變慢。

　　3.3.3 微分調節作用的分析

　　設Kp= 1、Ti= 0.01,討論Td= 10 ~ 100 時對系統階躍響應曲線的影響。輸人訊號階躍函式，分別進行模擬，如圖5 所展示的系統的階躍響應曲線。

　　圖5 單閉環調速系統PID控制階躍給定響應曲線

　　圖5 所顯示的模擬結果表明：根據單閉環調速系統的引數配合情況，起始上升段呈現較尖銳的波峰，Kp= 1、Ti= 0.01不變時，隨著Td值的加大，閉環系統的超調量增大，響應速度變慢。

　　4 .結論

　　（1）對於PID 引數採用MATLAB 進行整定和模擬，使用起來不僅快捷、方便，而且更為直觀，同時也避免了傳統方法反覆修改引數除錯。

　　（2）系統的響應速度會隨Kp值的增大而加快，同時也有助於靜差的減小，而Kp值過大則會使系統有較大超調，穩定性變壞；此外，系統的動作會因為過小的Kp值減慢。

　　（3）超調的減小、振盪變小以及系統穩定性的增加都取決於積分時間Ti的增大，但是系統靜差消除時間會因為Ti的增大而變長。

　　（4）增大微分時間Td對於系統的穩定性、系統響應速度的加快以及系統超調量的減小都會有所幫助。但是如果Td過大，則會使得調節時間較長，超調量也會增大；如果Td過小，同樣地也會發生以上狀況。

　　（5）總之PID 引數的整定必須考慮在不同時刻三個引數的作用以及彼此之間的作用關係。

(1)
確定比例係數Kp
確定比例係數Kp時，首先去掉PID的積分項和微分項，可以令Ti=0、Td=0，使之成為
純比例調節。輸入設定為系統允許輸出最大值的60％～70％，比例係數Kp由0開始逐漸增大，直至系統出現振盪；再反過來，從此時的比例係數Kp逐漸減小，直至系統振盪消失。記錄此時的比例係數Kp，設定PID的比例係數Kp為當前值的60％～70％。
(2)
確定積分時間常數Ti
比例係數Kp確定之後，設定一個較大的積分時間常數Ti，然後逐漸減小Ti，直至系統出現振盪，然後再反過來，逐漸增大Ti，直至系統振盪消失。記錄此時的Ti，設定PID的積分時間常數Ti為當前值的150％～180％。
(3)
確定微分時間常數Td
微分時間常數Td一般不用設定，為0即可，此時PID調節轉換為PI調節。如果需要設定，則與確定Kp的方法相同，取不振盪時其值的30％。
(4)
系統空載、帶載聯調
對PID引數進行微調，直到滿足效能要求。