完美的解釋了BP神經網路,自己要通過演算法計算一下
連結:https://zhuanlan.zhihu.com/p/24801814
來源:知乎
著作權歸作者所有。商業轉載請聯絡作者獲得授權,非商業轉載請註明出處。
在學習深度學習相關知識,無疑都是從神經網路開始入手,在神經網路對引數的學習演算法bp演算法,接觸了很多次,每一次查詢資料學習,都有著似懂非懂的感覺,這次趁著思路比較清楚,也為了能夠讓一些像我一樣疲於各種查詢資料,卻依然懵懵懂懂的孩子們理解,參考了樑斌老師的部落格BP演算法淺談(Error Back-propagation)(為了驗證樑老師的結果和自己是否正確,自己python實現的初始資料和樑老師定義為一樣!),進行了梳理和python程式碼實現,一步一步的幫助大家理解bp演算法!
為了方便起見,這裡我定義了三層網路,輸入層(第0層),隱藏層(第1層),輸出層(第二層)。並且每個結點沒有偏置(有偏置原理完全一樣),啟用函式為sigmod函式(不同的啟用函式,求導不同),符號說明如下:
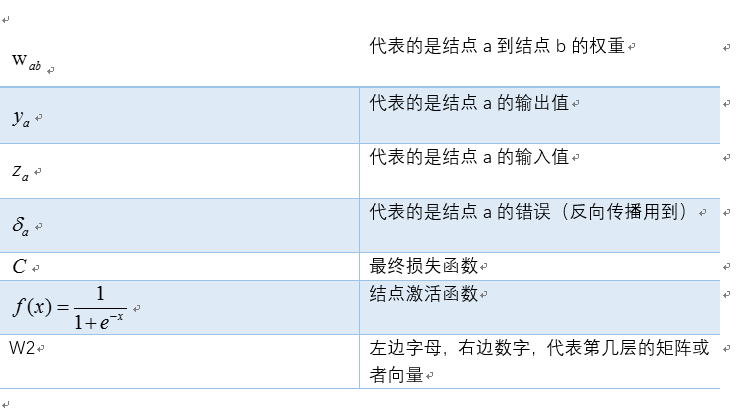
對應網路如下:
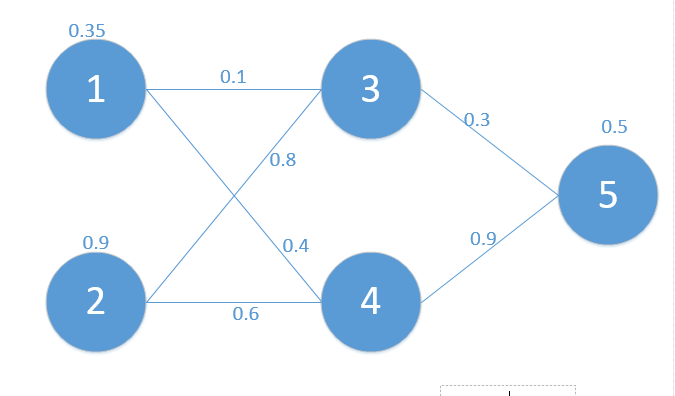 其中對應的矩陣表示如下:
其中對應的矩陣表示如下:
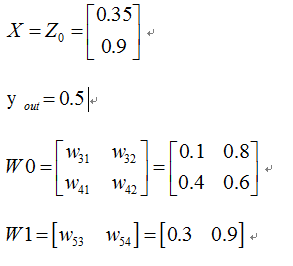 首先我們先走一遍正向傳播,公式與相應的資料對應如下:
首先我們先走一遍正向傳播,公式與相應的資料對應如下:

那麼:
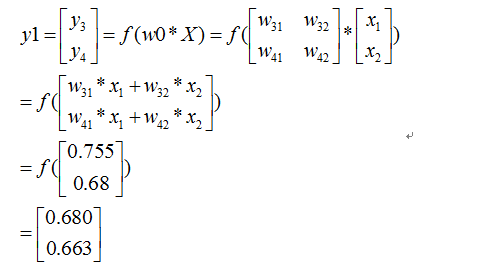
同理可以得到
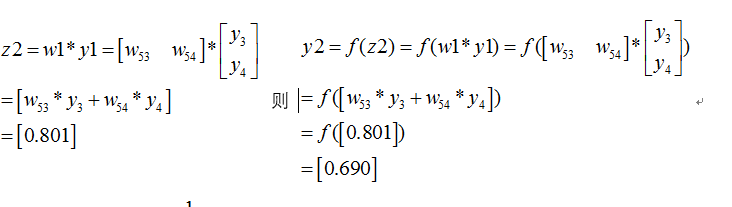 那麼最終的損失為
那麼最終的損失為
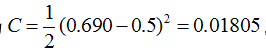
我們當然是希望這個值越小越好。這也是我們為什麼要進行訓練,調節引數,使得最終的損失最小。這就用到了我們的反向傳播演算法,實際上反向傳播就是梯度下降法中(為什麼需要用到梯度下降法,也就是為什麼梯度的反方向一定是下降最快的方向,我會再寫一篇文章解釋,這裡假設是對的,關注bp演算法)鏈式法則的使用。
下面我們看如何反向傳播
根據公式,我們有:
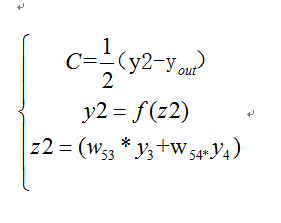 這個時候我們需要求出C對w的偏導,則根據鏈式法則有
這個時候我們需要求出C對w的偏導,則根據鏈式法則有
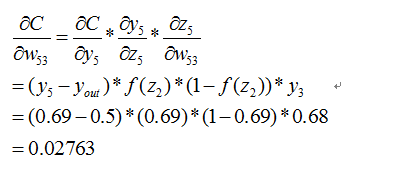
上面插入sigmod函式求導公式:
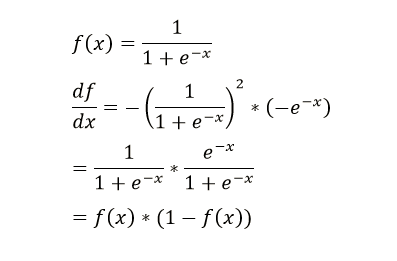 (在這裡我們可以看到不同啟用函式求導是不同的,所謂的梯度消失,梯度爆炸如果瞭解bp演算法的原理,也是非常容易理解的!)
(在這裡我們可以看到不同啟用函式求導是不同的,所謂的梯度消失,梯度爆炸如果瞭解bp演算法的原理,也是非常容易理解的!)
同理有
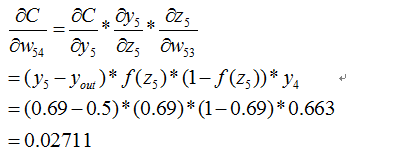
到此我們已經算出了最後一層的引數偏導了.我們繼續往前面鏈式推導:
我們現在還需要求
 下面給出其中的一個推到,其它完全類似
下面給出其中的一個推到,其它完全類似
 同理可得到其它幾個式子:
同理可得到其它幾個式子:
則最終的結果為:
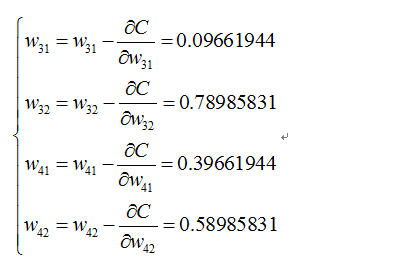
再按照這個權重引數進行一遍正向傳播得出來的Error為0.165
而這個值比原來的0.19要小,則繼續迭代,不斷修正權值,使得代價函式越來越小,預測值不斷逼近0.5.我迭代了100次的結果,Error為5.92944818e-07(已經很小了,說明預測值與真實值非常接近了
 好了,bp過程可能差不多就是這樣了,可能此文需要你以前接觸過bp演算法,只是還有疑惑,一步步推導後,會有較深的理解。
好了,bp過程可能差不多就是這樣了,可能此文需要你以前接觸過bp演算法,只是還有疑惑,一步步推導後,會有較深的理解。
---------------------------------------2017年1月29日更新----------------------------------------
應大量知友要求,給出分享連結
下面給出我學習bp時候的好的部落格
Backpropagation (裡面的插圖非常棒,不過好像有點錯誤,歡迎討論~)
上面實現的python程式碼如下:
import numpy as np
def nonlin(x, deriv=False):
if (deriv == True):
return x * (1 - x) #如果deriv為true,求導數
return 1 / (1 + np.exp(-x))
X = np.array([[0.35],[0.9]]) #輸入層
y = np.array([[0.5]]) #輸出值
np.random.seed(1)
W0 = np.array([[0.1,0.8],[0.4,0.6]])
W1 = np.array([[0.3,0.9]])
print 'original ',W0,'\n',W1
for j in xrange(100):
l0 = X #相當於文章中x0
l1 = nonlin(np.dot(W0,l0)) #相當於文章中y1
l2 = nonlin(np.dot(W1,l1)) #相當於文章中y2
l2_error = y - l2
Error = 1/2.0*(y-l2)**2
print "Error:",Error
l2_delta = l2_error * nonlin(l2, deriv=True) #this will backpack
#print 'l2_delta=',l2_delta
l1_error = l2_delta*W1; #反向傳播
l1_delta = l1_error * nonlin(l1, deriv=True)
W1 += l2_delta*l1.T; #修改權值
W0 += l0.T.dot(l1_delta)
print W0,'\n',W1
我也是在學習過程中,歡迎知友提出錯誤問題。真心希望加深大家對bp演算法的理解。
